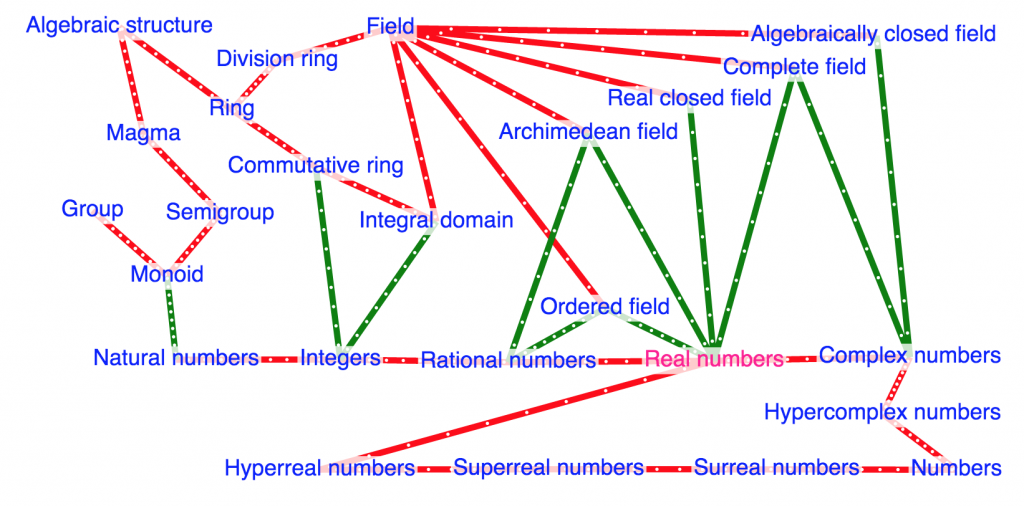
Some kinds of numbers (“<” means “subset of”): Natural numbers < Integers < Rational numbers < Real numbers < Hyperreal numbers < Superreal numbers < Surreal numbers < Numbers.
Real numbers < Complex numbers < Hypercomplex numbers < Numbers.
Some types of numbers (appearing in the diagram): Monoid < Semigroup < Magma < Algebraic structure. Integral domain < Commutative ring < Division ring < Ring < Algebraic structure. Ordered field < Field < Integral domain < Commutative ring < Ring < Algebraic structure. Archimedean field < Field. Complete field < Field. Real closed field < Field. Algebraically closed field < Field.
NOTE: Hyperreal numbers, Superreal numbers and Surreal numbers are examples of type Ordered field, Complete field and Real closed field. However, they are NOT examples of type Archimedean field, since they all contain infinitesimal numbers. The reason that these relations are not shown in the diagram is that displaying them would “clog up” the diagram with a lot of crossed links that would diminish its readability.
///////
Grundidé: Den röda delen av ovanstående diagram kallas Strävorna och representerar ett antal förslag på lektioner i den “lektionsgalax” som administreras av Nationellt Centrum för Matematikutbildning vid Göteborgs Universitet. Målsättnngen är att Strävorna ska bidra till att förbättra kvaliteten i matematikutbildningen i grundskolan och gymnasiet.
Den gröna delen av diagrammet representerar några tillägg till denna lektionsgalax skapade av olika personer (eller organisationer/företag) som haft tillgång till galaxens inre struktur. Tanken är att en eller några skolor, företag, kommuner, etc. ska kunna administera en begreppsgalax av något lämpligt slag samt kunna öppna upp den för bidrag utifrån av olika slag.
I ovanstående fall kan det t.ex. röra sig om lärare som har egna ideer om vad som kan bidra till att öka kvaliteten i matematikundervisningen, men generellt handlar det om att förbättra idéutbytet inom det eller de ämnesområden som är av intresse för galaxens operatör(er).
• Framtidens bibliotek
• Modeling learning
• Knowledge Gap Mapping
• NSDL: Nya Samarbetsformer i det Digitala Lärandelandskapet
• Learning vs. Embedment: The Core Problem for 21st Century Learning
Kunskapsmodellering och kunskapsmångfalder för ett lärande i förvandling
Vi lever i en ny tid där digitala medier tillhandahåller nya verktyg och möjliggör nya samarbetsmetoder som kan förändra vårt sätt att arbeta med information, kunskap och lärande. Detta är ett område som utvecklas mycket snabbt och som i Europa ofta kallas TEL. Den övergripande frågan i detta sammanhang är hur vi kan använda de nya möjligheterna för att öka effektiviteten i vårt livslånga lärande. Vår hypotes är att förutsättningarna för detta kan förbättras genom att vi alla, i egenskap av lärande individer, medverkar i (och tar med-ansvar för) upprättandet och utformandet av våra egna lärprocesser – ofta i form av olika typer av kontrakt med olika utbildningsleverantörer.
Den digitala utvecklingen har skapat ett samhälle där det formella och informella lärandet kan samverka i nya former. Tillgängliga tjänster och öppen information har satt användaren i centrum – inte bara som nyttjare utan också som medskapare av lärresurser. Detta innebär nya utmaningar för utbildningsinstitutioner, minnesinstitutioner och kunskapsförmedlande företag och organisationer inom public service.
Ett sätt att möta dessa utmaningar är att ta fram en ny form av strategisk kunskapsinfrastruktur, vilken stödjer den pågående utvecklingen där information i enskilda databaser länkas samman till en semantisk infrastruktur – och där ”informationen om informationen” (metadata) blir ”utpekningsbar” (dvs unikt identifierbar) från alla olika håll på nätet (genom att den förses med en s.k. URI). Detta gör att kunskaper och erfarenheter som är relaterade till globalt identifierbara ”saker och ting” blir delar av en globalt annoterad databas där beskrivningarna kan uppdateras inkrementellt (”change-by-increment”) genom att lägga till nya ingångar till (och utgångar från) det som fortfarande är aktuellt.
Denna kunskapsinfrastruktur ger förutsättningar för kontextualisering, sökningar, sammanställningar och analyser där meningsskapande helheter kan konstrueras utifrån komplexa och mångfacetterade informationsmängder. Därigenom förstärks spridningen och användningen av öppna kunskapsresurser med hög kvalitet.
Vi kallar denna typ av strukturering av kunskap för kunskapsmodellering, och resultatet av denna verksamhet för kunskapsmångfalder. En kunskapsmångfald kan betraktas som en sorts atlas av begreppsmässiga och sammanlänkade informationslandskap, vilket möjliggör navigation och presentation av sammanhang och innehåll med olika detaljrikedom och upplösning. Detta gör det möjligt att skapa överblick över kunskaper inom olika områden utan att därför behöva ge avkall på deras olika detaljer och djup.
Våra två semantiska kunskapsverktyg är begreppsbrowsern Conzilla som hanterar sammanhang (via s.k. ”sammanhangskartor”) och det elektroniska portföljsystemet Confolio som hanterar innehåll via mappar med (och länkar till) digitala lärresurser av olika slag.
I en värld av livslångt lärande, med ökande kostnader för formell utbildning och ökande variation i studenternas kunskapsbakgrunder blir det allt viktigare att kunna påverka utformningen av sina egna lärandeprocesser efter sina egna personliga förutsättningar och målsättningar. Detta ligger i linje med KTHs vision om det framtida kursutbudet som en sorts ”kunskapens smörgåsbord” i form av en sammanhängande kunskapsmångfald där alla kurser är valfria och där man är tydlig med vilka kunskapsgap som varje kurs syftar till att överbrygga. Sådan information kan med fördel uttryckas genom ”kursgapsmodellering”, dvs genom att beskriva ”före-och-efter-kunskaperna” för varje kurs eller kursavsnitt.
En viktig förbättringsmöjlighet för lärandet är möjligheten till vad vi kallar kunskapsaggregering, dvs möjligheten att fånga upp erfarenheter och aggregera (= lägga till) dem till den ursprungliga lärresursen på ett asynkront sätt. Lektioner kan idag spelas in och efterbehandlas i inlärningsförstärkande syfte. Dessutom kan kommentarer och feedback i form av reflektioner kring materialet spelas in, efterbearbetas och länkas till materialet i sin hittillsvarande form. Denna förbättringsinriktade kunskapsuppbyggnad ökar värdet hos lärresurserna och skapar ökad synlighet för resurser med hög (och empiriskt dokumenterad) verkningsgrad för lärande.
///////
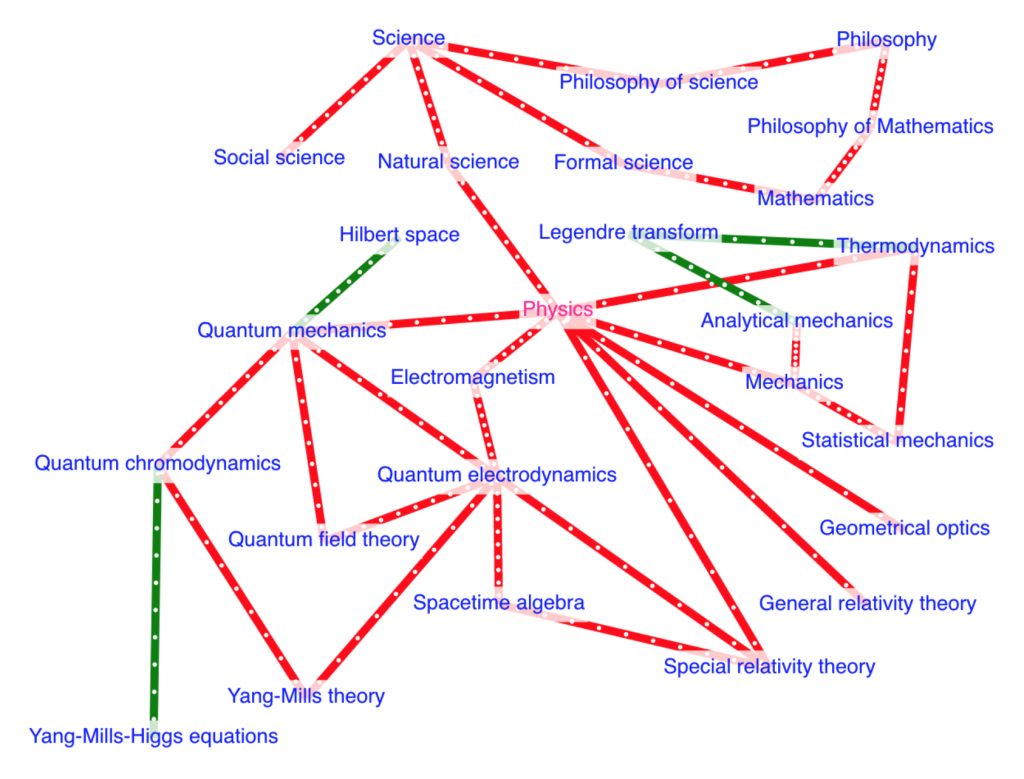
The aim of this diagram is to stimulate reflection and discussion of the scientific endeavours of physics (including its support by mathematics) within the larger contex of science and philosophy. For example, it is estimated that about half the engineers of the world are applying there knowledge of physics to create weapons of some kind. Does this reflect a “law of nature” or is there something that can be done to change it?
Considering the global challenges that we are facing because of climate change, how can we make sure that the rapidly increasing weaponization of the western world, due to the recent “special military operations” of Russia in Ukraine does not diminish or postpone the necessary actions to ensure a sustainable future for the world as we have come to know it.
• Climate change – a first attempt at a disagreement model
• Disagreement management
///////

///////
• History of mathematics
• History of algebra
• History of topos theory
• History of science
• History of Astronomy
• History of Chinese science and technology
• Egyptian mathematics
• Babylonian mathematics
• Greek mathematics
• Chinese mathematics
• Indian mathematics
• The Islamic golden age
• Science in the Renaissance
• The scientific revolution
• Mathematics during the scientific revolution
• Modern mathematics
• Future
• See also
///////
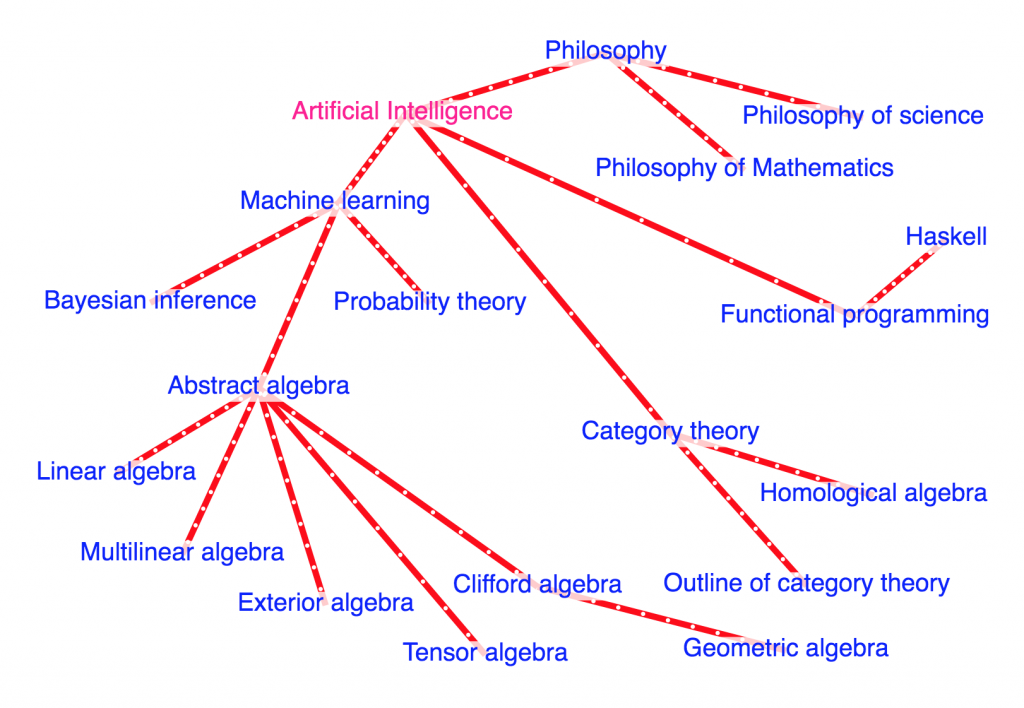
The aim of this diagram is to present some of the basic mathematics behind artificial intelligence and to connect it with the philosophy of science and mathematics that lies behind the development of this very powerful and potentially dangerous field.
• Artificial ethics
• Digital bolshevism
• Rage inside the machine
///////
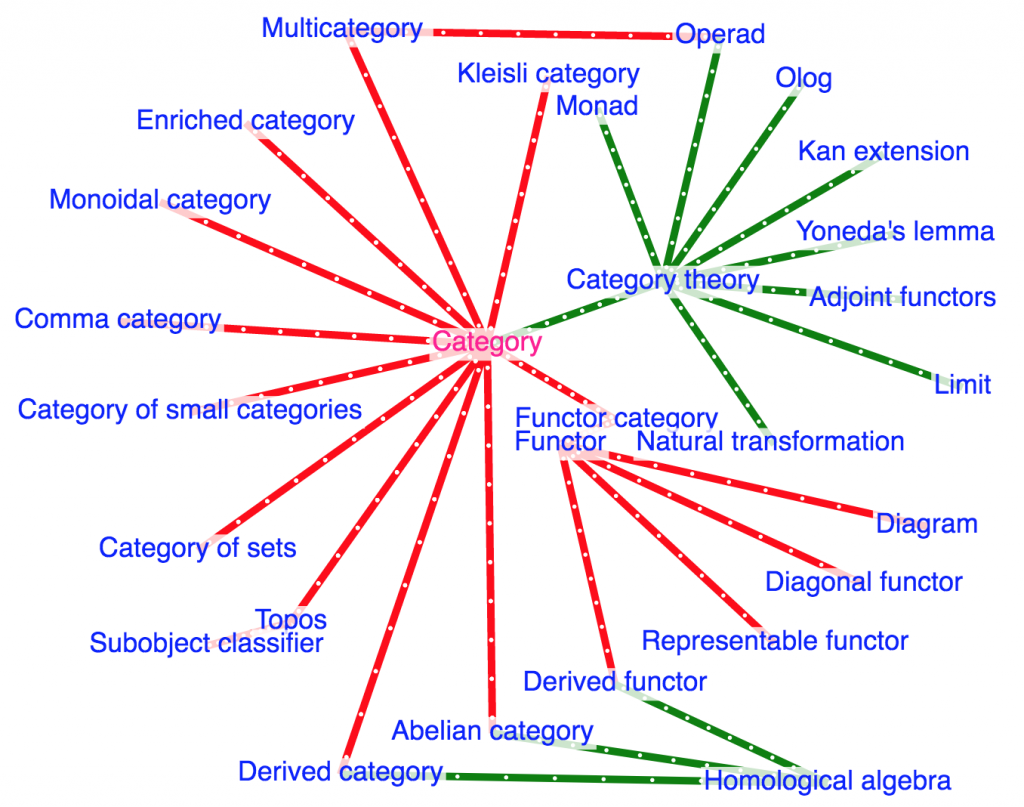
///////
A Euclidean space E is characterised by two three basic things.
• (1): E is a finite-dimensional vector space.
• (2): E has a metric which measures the distance between any two of its points.
• (3): E is complete, which means that any sequence that tries to converge, i.e., any Cauchy sequence a_n , manages to do so within E, that is, there is a point a in E such that the points of the sequence get arbitrarily close to a when n is large enough. This property is often describe as “the tail of a_n gets arbitrarily close to a .
The aim of this diagram is to study what happens when a Euclidean space
///////