This page is a sub-page of our page on Calculus of One Real Variable.
///////
The sub-pages of this page are:
• Differentiable versus Fractal Curves
///////
Related KMR pages:
• Differentiation and Affine Approximation (in Several Real Variables)
• The Chain Rule (in One Real Variable)
• Big-Ordo and Little-ordo notation
///////
Other related sources of information:
• Derivative (at Encyclopedia Britannica Demystified)
• Definition of derivative as best affine approximation
• Little-o notation
• Logarithmic differentiation
• Limits, L’Hopital’s rule, and epsilon delta definitions (Steven Strogatz on YouTube)
///////
The interactive simulations on this page can be navigated with the Free Viewer
of the Graphing Calculator.
///////
Anchors into the text below:
• Differentiation of a function of one real variable
• Macrofication
• The derivative as the limit of a quotient of differences
• The derivative as the slope of a curve
• Reinterpreting the derivative for multidimensional extension
• Affine Maps
• Affine Approximation
• Basic diagram for an affine approximation
• Affine approximation in one dimension
• The derivative as the linear part of the affine approximation
• Notation adapted to the pullback x = x(u)
• The paradox of the derivative
///////
Differentiation of a function of one real variable
NOTE: For a function of one variable, differentiation means computing the derivative of the function. For a function of several variables, there are several kinds of derivatives, and differentiation then means computing the total derivative of the function.
///////
Plot derivative:
The interactive simulation that created this movie
///////
Macrofication:
From \, micro(\textcolor{blue}{x_0}) \, to \, macro(\textcolor{blue}{x_0}) :
\, \Delta f \equiv f(\textcolor{blue}{x_0} + \textcolor{red}{\Delta x}) - f(\textcolor{blue}{x_0}) = {f'(x)}_{\textcolor{blue}{x_0}} \, \textcolor{red}{\Delta x} + o( | \textcolor{red}{\Delta x} | ) .
In calculus, selecting a fixed point \, \textcolor{blue}{x_0} \, from the values of a moving point \, x \, means going from \, {macro}_{ \, x} \, to \, {micro}_{ \, \textcolor{blue}{x_0}} \, , whatever space that \, x \, is “living in” (= is a member of).
///////
The derivative as the limit of a quotient of differences
The derivative as the limit of the quotient between a dependent
and an independent difference when the latter goes to zero:
\, f'(x_0) = \lim\limits_{\Delta x \to 0} \dfrac{f(x_0 + \Delta x) - f(x_0)} {(x_0 + \Delta x) - x_0 } \, = \, \lim\limits_{\Delta x \to 0} \dfrac{f(x_0 + \Delta x) - f(x_0)} { \Delta x } .
With this definition, based on the concept of limit, the derivative of a function \, \mathbb{R} \ni x \mapsto f(x) \in \mathbb{R} \, at the point \, x = x_0 \, can be interpreted as a measure of the rate of change of \, f \, when the point \, x \, varies within an infinitesimal (= “infinitely small”) neighborhood of the point \, x_0 .
As an example, the velocity \, v(t) \, at time \, t = t_0 \, of a vehicle, whose position at time \, t \, is given by the function \, \mathbb{R} \ni t \mapsto f(t) \in \mathbb{R} \, , can be expressed as:
\, v(\textcolor{blue}{t_0}) = f'(t)_{\textcolor{blue}{t_0}} = \lim\limits_{\textcolor{red}{\Delta t} \to 0} \dfrac{f(\textcolor{blue}{t_0} + \textcolor{red}{\Delta t}) - f(\textcolor{blue}{t_0})} {\textcolor{red}{\Delta t}} \, .
The derivative as the slope of a curve:
Geometrically, the above definition of the derivative as the limit of a certain difference quotient is consistent with regarding the derivative of a function at a certain point as the slope of the tangent to the graph of the function at that point.
/////// Quoting Derivative at Encyclopedia Britannica Demystified:
Geometrically, the derivative of a function can be interpreted as the slope of the graph of the function or, more precisely, as the slope of the tangent line at a point. Its calculation, in fact, derives from the slope formula for a straight line, except that a limiting process must be used for curves.
/////// End of quote from “Derivative” at Encyclopedia Britannica Demystified.
Normally this is the first definition of the concept of derivative that a student encounters, most often at the high school level. As we have seen, it provides convenient representations of various “rate-of-change-related” concepts – such as for example “velocity” or “power”.
The problem with the slope-of-the-tangent interpretation of the derivative of a function is that it does not “extend naturally” to several dimensions where there are different slopes in different directions. In order to prepare for such an extension, which provides one of the cornerstones of the calculus of several variables, we need to think of the concept of derivative from another perspective. This perspective is based on the concept of affine approximation of the behavior of a function within a small neighborhood of a selected point on its graph.
Functions of several variables have graphs that live in spaces of several dimensions. Hence, when studying the behavior of such functions, one has to deal with transformations between spaces of several dimensions, as well as with approximations of such transformations.
Reinterpreting the derivative for multidimensional extension
What is Jacobian? | The right way of thinking derivatives and integrals
(Mathemaniac on YouTube):
/////// Connect with Affine Geometry.
In order to facilitate the generalization to many dimensions we need to make a slight change of notation in comparison with the slope-based notation used above. The fixed point \, x_0 \, will be given a non-indexed name, for example \, p . The reason behind this change is that the fixed point will now have many components, and if we were to call it \, x_0 , then for compatibility reasons we would have to call these components something like \, {x_0}_1, {x_0}_2, \, \cdots \, {x_0}_n \, which would be both cumbersome and confusing.
Affine Maps
Let \, X \, and \, Y \, be two vector spaces over the same scalars. In what follows, the point \, \textcolor{blue}{p} \in X \, is to be regarded as fixed whereas the point \, x \in X \, is to be regarded as varying in a small neighborhood of \, \textcolor{blue}{p} . The difference \, x - \textcolor{blue}{p} \, will be referred to as the input disturbance and denoted by \, \, \textcolor{red}{\Delta x} .
Definition: An affine map \, A_{\textcolor{blue}{p}} \, : X \rightarrow Y \, consists of the ordered application of :
(1): A constant map \, T_{\textcolor{blue}{p}} : x \mapsto x + \textcolor{blue}{p} .
This map is called a displacement (or a translation) by \, \textcolor{blue}{p} .
(2): A linear map \, L : x - \textcolor{blue}{p} \mapsto L(x - \textcolor{blue}{p}) \,
of the input disturbance \, x - \textcolor{blue}{p} = \textcolor{red}{\Delta x} .
Hence we have: \, A_{\textcolor{blue}{p}}(x) \stackrel{\text {def}}{=} T_{\textcolor{blue}{p}} + L(x - \textcolor{blue}{p}) .
The translations form a vector space \, V , and each translation acts on the vectors \, x \in X by displacing them additively.
Hence, for each pair of translation vectors \, T_1, T_2 \in V and each vector \, x \in X , we have
\, T_1(T_2(x)) = T_2(T_1(x)) = (T_1 + T_2)(x) .
///////
Affine Approximation:
Definition: Let \, \textcolor{green} {\overrightarrow {O,P}} \, be the translation taking \, (0, 0) \, to \, (\textcolor{blue}{p}, f(\textcolor{blue}{p})) .
The function \, f_{\textcolor{blue}{p}}(x) \stackrel{\text{def}}{=} f(\textcolor{blue}{p}) + f'(x)_{\textcolor{blue}{p}} \,(x - \textcolor{blue}{p}) \,
is called the affine approximation of \, f \, at the point \, \textcolor{blue}{p} .
The reason behind the determinate article “the” in this name is the following
Theorem: \, | f(x) - f_{\textcolor{blue}{p}}(x) | = \, \, o( | x - \textcolor{blue}{p} | ) \, when \, | x - \textcolor{blue}{p} | \rightarrow 0 ,
and \, f_{\textcolor{blue}{p}} \, is the only affine map with this property.
Geometrically, this uniqueness corresponds to the fact that ALL the other affine maps through the point \, (\textcolor{blue}{p}, f(\textcolor{blue}{p})) \, represent lines that intersect the graph of the function \, f \, transversally (= non-tangentially) at this point.
///////
Basic diagram for an affine approximation:
\, \begin{matrix} Y & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\; f \;\;\;\;\;\;\;\;\;\;\;\;\;}} & X \\ \uparrow & & \uparrow \\ f(x) & {\xleftarrow{\, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & x \\ & & & \\ Y_{f(\textcolor{blue} {p})} & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\; f_{\textcolor{blue}{p}} \;\;\;\;\;\;\;\;\;\;\;}} & X_{\textcolor{blue}{p}} \\ \uparrow & & \uparrow \\ f(\textcolor{blue} {p}) + f'(x)_{\textcolor{blue} {p}} \, \textcolor{red} {\Delta x} & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & {\textcolor{blue}{p} + \textcolor{red} {\Delta x}} \end{matrix} .
Note: The “forward” direction is represented “from the right to the left”. The reason for this is to be compatible with the matrix algebra that will emerge through the chain rule.
///////
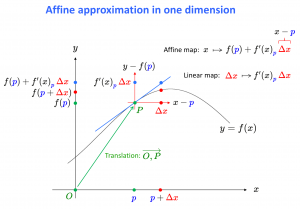
Affine approximation in one dimension:
The interactive simulation that created this movie
///////
The interactive simulation that created this movie
///////
The affine approximation of a differentiable function \, f : {\mathbb{R}}^1 \leftarrow {\mathbb{R}}^1
in the neighborhood of a point \, \textcolor{blue}{p} \, \in {\mathbb{R}}^1 \, is defined by
\, f_{\textcolor{blue}{p}}(x) \stackrel{\text{def}}{=} f(\textcolor{blue}{p}) + {f'(x)}_{\textcolor{blue}{p}} \, (x - \textcolor{blue}{p}) \, \equiv \, f(\textcolor{blue}{p}) + {f'(x)}_{\textcolor{blue}{p}} \, \textcolor{red} {\Delta x} .
The characteristic property of the affine approximation \, f_{\textcolor{blue}{p}} \, can be expressed as:
\, f(x) = f_{\textcolor{blue}{p}}(x) + o(|x - \textcolor{blue}{p}|) \, when \, x \, is close enough to \, \textcolor{blue}{p} .
///////
The derivative as the linear part of the affine approximation:
We are now in a position to give a definition of the derivative of a function which is equivalent to the “slope definition” in the one-dimensional case, but which, in contrast to the slope definition, extends naturally to several dimensions:
New Definition: The derivative of a function \, f \, at a given point \, \textcolor{blue}{p} \,
is the linear part of its affine approximation \, f_{\textcolor{blue}{p}} .
The derivative is well defined because: The affine approximation \, f_{\textcolor{blue}{p}} \, is the only affine map through the point \, (\textcolor{blue}{p}, f(\textcolor{blue}{p})) \, whose line intersects the graph of the function \, f \, non-transversally at this point, since this line is the only line that is tangent to the graph of the function \, f \, there.
We have now managed to redefine the derivative in a way that is equivalent to the old definition in the one-dimensional case (more about this below), but which generalizes immediately to several dimensions.
For example, if we have a function \, f : \mathbb{R}^2 \rightarrow \mathbb{R}^1 , then the graph of the affine approximation \, f_{\textcolor{blue}{p}} \, is a plane through the point \, (\textcolor{blue}{p}, f(\textcolor{blue}{p})) , and this plane is the only plane through the point \, (\textcolor{blue}{p}, f(\textcolor{blue}{p})) \, that is tangent to the graph of \, f \, (which is a surface) at this point.
In higher dimensions the planes are called hyperplanes and the surfaces are called hypersurfaces, but the same uniqueness condition applies: The hyperplane of the affine approximation \, f_{\textcolor{blue}{p}} \, is the only hyperplane that is tangent to the hypersurface of \, f \, at the point \, (\textcolor{blue}{p}, f(\textcolor{blue}{p})) .
///////
\, f( \textcolor{blue}{p} + \textcolor{red}{\Delta x} ) = f_{\textcolor{blue}{p}}(x) + o( | \textcolor{red}{\Delta x} | ) = f(\textcolor{blue}{p}) + {f'(x)}_{\textcolor{blue}{p}} \, \textcolor{red}{\Delta x} + o( | \textcolor{red}{\Delta x} | ) \, .
///////
Notation adapted to the pullback \, x = x(u) \, :
Basic diagram for an affine approximation:
\, \begin{matrix} Y & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\; f \;\;\;\;\;\;\;\;\;\;\;\;\;}} & X \\ \uparrow & & \uparrow \\ f(x) & {\xleftarrow{\, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & x \\ & & & \\ Y_{f(\textcolor{blue} {p})} & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\; f_{\textcolor{blue}{p}} \;\;\;\;\;\;\;\;\;\;\;}} & X_{\textcolor{blue}{p}} \\ \uparrow & & \uparrow \\ f(\textcolor{blue} {p}) + f'(x)_{\textcolor{blue} {p}} \, \textcolor{red} {\Delta x} & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & {\textcolor{blue}{p} + \textcolor{red} {\Delta x}} \end{matrix}
Note: The “forward” direction is represented “from the right to the left”. The reason for this is to be compatible with the matrix algebra that will emerge through the chain rule.
Backward expansion of the basic diagram to the right by the substitution \, x = x(u) ,
which is a pullback of the variable \, x \, :
\, \begin{matrix} Y & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\; f \;\;\;\;\;\;\;\;\;\;\;\;\;}} & X & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\; x \;\;\;\;\;\;\;\;\;\;\;\;\;}} & U \\ \uparrow & & \uparrow & & \uparrow \\ f(x(u)) & {\xleftarrow{\, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & x(u) & {\xleftarrow{\, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & u \\ & & & & & & & \\ Y_{f(x(\textcolor{blue} {p}))} & {\xleftarrow{\;\;\;\;\;\;\;\;\; f_{x(\textcolor{blue} {p})} \;\;\;\;\;\;\;\;\;}} & X_{x(\textcolor{blue} {p})} & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\; x_{\textcolor{blue}{p}} \;\;\;\;\;\;\;\;\;\;\;}} & U_{\textcolor{blue}{p}} \\ \uparrow & & \uparrow & & \uparrow \\ & & x(\textcolor{blue} {p}) + x'(u)_{\textcolor{blue} {p}} \, \textcolor{red} {\Delta u} & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & {\textcolor{blue}{p} + \textcolor{red} {\Delta u}} \\ f(x(\textcolor{blue} {p})) + f'(x)_{x(\textcolor{blue} {p})} \, \textcolor{red} {\Delta x} & { \xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & x(\textcolor{blue} {p}) + \textcolor{red} {\Delta x} & & \\ & & & & & & & \\ Y_{f(x(\textcolor{blue} {p}))} & & {\xleftarrow{\, { \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (f \circ x)}_{\textcolor{blue}{p}} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; } } & & U_{\textcolor{blue}{p}} \\ \uparrow & & & & \uparrow \\ (f \circ x)(\textcolor{blue} {p}) + {(f \circ x)'(u)}_{\textcolor{blue} {p}} \, \textcolor{red} {\Delta u} & & {\xleftarrow{\, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & & {\textcolor{blue}{p} + \textcolor{red} {\Delta u}} \end{matrix}
///////
x = x(u):
\, x(\textcolor{blue}{p} + \textcolor{red}{\Delta u}) = x(\textcolor{blue}{p}) + {x'(u)}_{\textcolor{blue}{p}} \, \textcolor{red}{\Delta u} + o( | \textcolor{red}{\Delta u} | ) \, .
(f°x)(u) = f(x(u)):
\, (f \circ x)(\textcolor{blue}{p} + \textcolor{red}{\Delta u}) = f(x(\textcolor{blue}{p} + \textcolor{red}{\Delta u})) = f(x(\textcolor{blue}{p})) + {f'(x)}_{x(\textcolor{blue}{p})} \, {x'(u)}_{\textcolor{blue}{p}} \, \textcolor{red}{\Delta u} + o( | \textcolor{red} {\Delta u} | ) \, .
///////
The paradox of the derivative (Essence of calculus)
(Steven Strogatz = 3Blue1Brown) on YouTube:
///////
It’s an awesome post for all the web viewers; they will take advantage from it I am sure.
Simply desire to say your article is as astonishing. The clarity in your post is just spectacular and i can assume you are an expert on this subject. Well with your permission let me to grab your RSS feed to keep updated with forthcoming post. Thanks a million and please carry on the enjoyable work.