This page is a sub-page of the page on Knowledge Management.

////////

The sub-pages of this page are:

• Systems Modeling
• Political Modeling
• Provocative Modeling
• Knowledge Mapping
• Metadata Modeling
• Modeling Learning
• Modeling Change
• Conceptual Modeling
• Social Modeling for Social Mediation

///////

Related KMR pages:

• Knowledge Negotiations
• Disagreement Management
• Collectigence
• Common Sense

• Asynchronous Public Service
• From Opiniocracy to Visionocracy

• TELL ME

• Mathematics is Representation
• Category Theory
• The Human Category

• The Universal Knowledge Evolution Formula

• CHARGE (Cultural Heritage Asynchronous Research Grid Environment)
• MATCH (MAthematical Transformations for Cultural Heritage)
• Framtidens Bibliotek

• David Hestenes on Modeling

///////

Other sources of related information:

• A Modeling Primary on Methods and Techniques for Communicative Modeling
and Disagreement Management. [TEL-Map D1.1, Febr. 2011]

///////

/////////////////////////////////////////////////////////////////////
Modeling is the art of disregarding as much as possible
in such a way that it is noticed as little as possible
//////////////////////////////////////////////////////////////

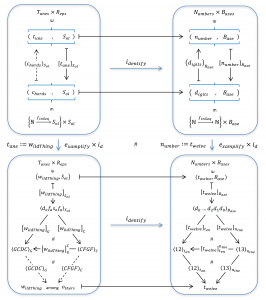
Representation and Reconstruction of a Representee with respect to a Base:

Representation: [ \, p_{resentant} \, ]_{P_{aradigm}} \, = \, \left< \, r_{epresentant} \, \right>_{P_{aradigm}} \, = \, \left< \, m_{odel} \, \right>_{P_{aradigm}}

A total representation enables a

Total Reconstruction: \left( \, \left< \, r_{epresentant} \, \right>_{P_{aradigm}} \, \right)_{P_{aradigm}} \, = \, p_{resentant}

Non-total representations are called partial, because they allow partial reconstruction of the presentant (see below).

///////

P_{aradigm} = B_{ackground} = B_{ase} = B_{asis} = ...

Representation: [ \, p_{resentant} \, ]_{B_{ackground}} \, = \, \left< \, f_{oreground} \, \right>_{B_{ackground}} \, = \, \left< \, i_{mage} \, \right>_{B_{ackground}}

Representation: [ \, G_{round} \, ]_{B_{ack}G_{round}} \, = \, \left< \, G_{round}R_{epresentation} \, \right>_{B_{ack}G_{round}}

Representation: [ \, B_{ackground} \, ]_{C_{onzilla}} \, = \, \left< \, C_{ontext}, P_{urpose}, T_{argetgroup} \, \right>_{C_{onzilla}}

///////

Representation:

[ \, B_{ack}G_{round} \, ]_{B_{ack}(B_{ack}G_{round})} \, = \, \left< \, (B_{ack}G_{round})R_{epresentation} \, \right>_{B_{ack}(B_{ack}G_{round})}

///////

PARTIAL REPRESENTATIONS

An example from the labour market:

Representation: [ \, e_{mployee} \,]_{L_{abourLaw}} = \left< \, e_{mployeeConcept} \, \right>_{L_{abourLaw}}

Partial Reconstruction: \left( \, \left< \, e_{mployeeConcept} \, \right>_{L_{abourLaw}} \, \right)_{L_{abourLaw}} = e_{{mployee}_{LL}}

///////

Representation: [ \, e_{mployee} \,]_{T_{axLaw}} = \left< \, e_{mployeeConcept} \, \right>_{T_{axLaw}}

Partial Reconstruction: \left( \, \left< \, e_{mployeeConcept} \, \right>_{T_{axLaw}} \, \right)_{T_{axLaw}} = e_{{mployee}_{TL}}

///////

IMPORTANT: Both of these representations are partial, which means that an employee cannot be uniquely reconstructed from neither its WorkLaw nor its TaxLaw representation. In general we have \, e_{{mployee}_{LL}} \not = e_{{mployee}_{TL}} \not = e_{mployee} .

RESPONSE: These representations have different contexts, purposes, and target groups. The modeling process should therefore focus on behaviour (that is described by VERBS) and not on properties (that are described by NOUNS and ADJECTIVES).

/////// In Swedish:

Ett Exempel Från Arbetsmarknaden:

Representation: [ \, a_{rbetstagare} \,]_{A_{rbetsRätt}} = \left< \, a_{rbetstagarBegrepp} \, \right>_{A_{rbetsRätt}}

Partiell Rekonstruktion: \left( \, \left< \, a_{rbetstagarBegrepp} \, \right>_{A_{rbetsRätt}} \, \right)_{A_{rbetsRätt}} = a_{{rbetstagare}_{AR}}

///////

Representation: [ \, a_{rbetstagare} \, ]_{S_{katteRätt}} = \left< \, a_{rbetstagarBegrepp} \, \right>_{S_{katteRätt}} \,

Partiell Rekonstruktion: \left( \, \left< \, a_{rbetstagarBegrepp} \, \right>_{S_{katteRätt}} \, \right)_{S_{katteRätt}} = a_{{rbetstagare}_{SR}} \,

///////

VIKTIGT: Båda dessa representationer är partiella, vilket betyder att arbetstagaren inte kan unikt rekonstrueras från vare sig sin arbetsrättsliga eller sin skatterättsliga representation.
I allmänhet gäller \, a_{{rbetstagare}_{AR}} \not = a_{{rbetstagare}_{SR}} \not = a_{rbetstagare} .

RESPONS: Dessa representationer har olika sammanhang, syfte(n), och målgrupp(er). Modelleringsfokus bör därför ligga på beteenden (som beskrivs med VERB) och inte på egenskaper (som beskrivs med SUBSTANTIV och ADJEKTIV).

///////

Representation: [ \, A_{rbetsRätt} \, ]_{C_{onzilla}} = \left< \, S_{{ammanhang}_{AR}}, S_{{yfte}_{AR}}, M_{{ålgrupp}_{AR}} \, \right>_{C_{onzilla}}

Representation: [ \, S_{katteRätt} \, ]_{C_{onzilla}} = \left< \, S_{{ammanhang}_{SR}}, S_{{yfte}_{SR}}, M_{{ålgrupp}_{SR}} \, \right>_{C_{onzilla}}

/////// Back to English:

Representation: [ \, L_{abourLaw} \, ]_{C_{onzilla}} = \left< \, C_{{ontext}_{LL}}, P_{{urpose}_{LL}}, T_{{argetgroup}_{LL}} \, \right>_{C_{onzilla}}

Representation: [ \, T_{axLaw} \, ]_{C_{onzilla}} = \left< \, C_{{ontext}_{TL}}, P_{{urpose}_{TL}}, T_{{argetgroup}_{TL}} \, \right>_{C_{onzilla}}

///////

Process B is naturally related to process A:

///////

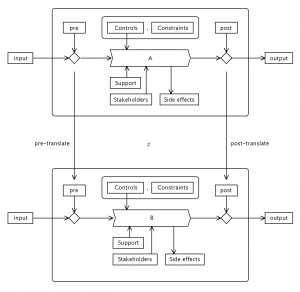
Numbers are naturally related to Music:

///////

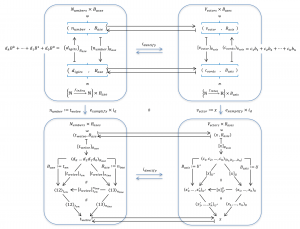
Numbers and Vectors are naturally related to each other.

Hence Numbers and Vectors are naturally equivalent.

///////

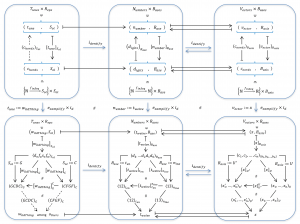
Numbers and Vectors are naturally related to Music:

///////