Projective Geometry | Knowledge Management Research Group

This is a sub-page of our page on Geometry.

///////

The sub-pages of this page are:

• Projective Metrics

///////

Related KMR-pages:

• The Euclidean Degeneration
• Metric Geometry
• Affine Geometry
• Linear Algebra

///////

Books:

• Jürgen Richter-Gebert (2011), Perspectives on Projective Geometry – A Guided Tour Through Real and Complex Geometry, Springer, ISBN 978-3-642-17285-4.
• W. T. Fishback (1969), Projective and Euclidean Geometry, John Wiley & Sons, Inc.,
ISBN 13: 978-047126-053-0.
• H. Winroth (1999), Dynamic Projective Geometry, PhD thesis at NADA/KTH.

///////

Other relevant sources of information:

• Projective geometry
• Homogeneous coordinates
• Cross ratio
• Homography
• Cayley transform
• Collineation
• Fundamental theorem of projective geometry
• Pole and polar
• Semilinear transformation
• Cayley-Klein metric

• Dynamic Projective Geometry (PhD-thesis of Harald Winroth, KTH, 1999)

///////

The interactive simulations on this page can be navigated with the Free Viewer
of the Graphing Calculator.

///////

History of projective geometry:

• Felix Klein
• Arthur Cayley
• Julius Plücker
• August Ferdinand Möbius
• Jacob Steiner
• Karl Georg Christian von Staudt
• Joseph Diez Gergonne
• Jean-Victor Poncelet
• Blaise Pascal
• Girard Desargues
• Kepler’s idea for projective geometry
• Piero della Francesca
• Leon Battista Alberti
• Filippo Brunelleschi
• Omar Khayyam
• Ibn al-Haytham (Alhazen)
• Pappus of Alexandria

• History of perspective (at Op.Art)
• History of perspective (at Slideshare)
• A Brief History of Perspective (at classicalart.org)
• Brunelleschi’s Peepshow and the Origins of Perspective

///////

The interactive simulations on this page can be navigated with the Free Viewer
of the Graphing Calculator.

///////

Representation: $[ \, l_{ine} \, ]_{E_{uclidean \, Geometry}} \, = \, \left< \, a_{ffine} \, l_{inear} \, e_{quation} \, \right>_{E_{uclidean \, Geometry}}$

Representation: $[ \, p_{oint} \, ]_{P_{rojective \, Geometry}} \, = \, \left< \, h_{omogeneous} \, l_{inear} \,e_{quation} \, \right>_{P_{rojective \, Geometry}}$

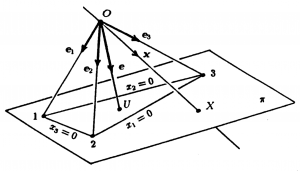
Representation: $[ \, p_{oint} \, ]_{\mathbb{P}^2} \, = \, \left< \, l_{ine} \, o_{n} \, t_{he} \, p_{oint} \, O \, \right>_{{\mathbb{E}^3}_O}$

Representation: $[ \, p_{oint} \, ]_{\mathbb{P}^2} \, = \, \left< \, h_{omogeneous} \, l_{inear} \, e_{quation} \, \right>_{\mathbb{P}^2}$

Representation: $[ \, l_{ine} \, ]_{\mathbb{P}^2} \, = \, \left< \, p_{lane} \, o_{n} \, t_{he} \, p_{oint} \, O \, \right>_{{\mathbb{E}^3}_O}$

///////

$x^2 + y^2 = 0 \,\, [ \, \Rightarrow \, ]_{\mathbb{R}} \,\, x = 0, y = 0 \,$ .

$x^2 + y^2 = 0 \,\, [ \, \Rightarrow \, ]_{\mathbb{C}} \,\, y = ix, y = -ix \,$ .

///////

Reconstruction: $\left( \, \left< \, m_{odel} \, \right>_{P_{aradigm}} \, \right)_{P_{aradigm}} \, = \, r_{epresentee}$

///////

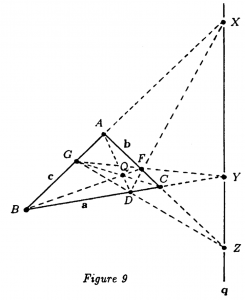
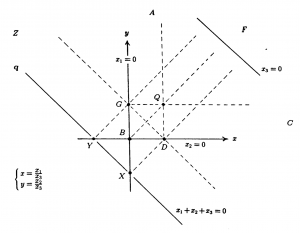
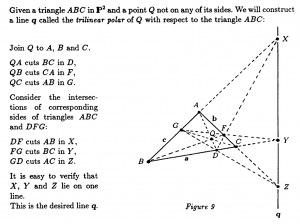
General trilinear polarity in $\, \mathbb{P}^2 \,$ :

///////

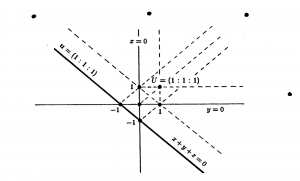
Cartesian trilinear polarity in $\, \mathbb{R}^2 \,$ :

///////

Trilinear Polars and Harmonic Nets (Richard Southwell on YouTube):

///////

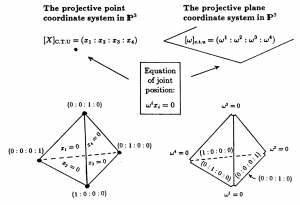
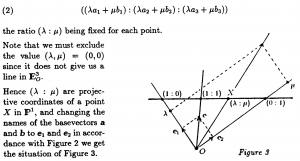
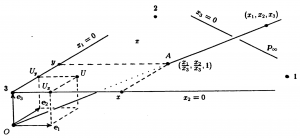
The projective point- and plane-coordinate systems in $\, \mathbb{P}^3 \,$ :

///////

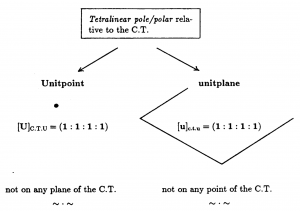
Dual unification in $\, \mathbb{P}^3 \,$
by the tetralinear pole-polar relationship
between the unit point and the unit plane:

///////

Plane projective CTU in $\mathbb{P}^2 \,$ :

///////

Line-projective CIU in $\mathbb{P}^1 \,$ :

///////

Plane euclidean CTU in $\mathbb{R}^2 \,$ :

///////

Trilinear euclidean pole-polar relation in $\mathbb{R}^2 \,$ :

///////

Trilinear projective pole-polar relation in $\mathbb{P}^2 \,$ :

///////

d-Grassmannians and their degrees of freedom in $\mathbb{P}^n \,$ :

///////

Complete Quadrangle:

///////

This film shows the parallelogram (in white) that is formed by the midpoints of the four sides of a generic quadrangle in 3D.

The interactive simulation the created this movie.

///////

Projective Triangle – connected regions:

Interactive simulation of Projective Triangle – connected regions.

///////

Conic sections:

NOTE: Ellipses, parabolas and hyperbolas are not separate objects in projective geometry, since they can all be projected into each other. Hence, in projective geometry, we can only talk about “conics”.

The interactive simulation that created this movie.

///////

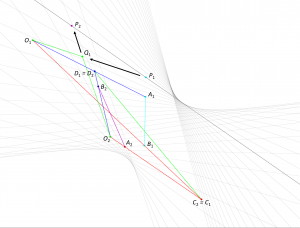
Perspective range-to-range transformation:

A perspective range-to-range transformation describes a point as an envelope of lines.

Two ranges can only be perspective from a point
if this point does not belong to anyone of the two ranges.

The interactive simulation that created this movie.

///////

Projective range-to-range transformation:

The interactive simulation that created this movie.

///////

The fundamental theorem of projective geometry:

Two projectively related ranges
determine the line-locus (= the envelope) of a unique conic.

In general, a conic is determined by five lines in generic position.

///////

Conics via projective geometry (N. J. Wildberger on YouTube):

///////

Projective range-to-range transformation (elliptic envelope 1):

The interactive simulation that created this movie.

///////

A non-degenerated projective range-to-range transformation
determines a conic envelope (an ellipse in the depicted case):

///////

A non-degenerated projective range-to-range transformation
determines a conic envelope (a hyperbola in the depicted case):

///////

The interactive simulation that created this movie.

///////

A degenerated projective range-to-range transformation
is called a perspective range-to-range transformation
and it determines a point as an envelope of lines.

///////

A perspective range-to-range transformation
describes a point as an envelope of lines:

The interactive simulation that created this movie.

///////

DUALITY

///////

The dual version of the fundamental theorem:

A projective pencil-to-pencil transformation determines a conic
as a point-locus (= an ellipse in the depicted case):

Two projectively related pencils determine the point-locus of a unique conic.
This conic is often referred to as the Steiner conic.

In general, a conic is determined by five points in generic position.

The interactive simulation that created this movie.

///////

A projective pencil-to-pencil transformation determines a conic
as a point-locus (= a hyperbola in the depicted case):

The interactive simulation that created this movie.

///////

A non-degenerated projective transformation is called a projectivity. It can be shown that any projectivity can be expressed as the product of at most two different perspective transformations. If the projectivity degenerates, it becomes a perspective transformation, and in this case it is called a perspectivity.

///////

A perspective pencil-to-pencil transformation determines a line as a locus of points: