This page is a sub-page of our page on Vector spaces.
///////
The sub-pages of this page are:
• …
///////
Related KMR-pages:
• Topology
• Topological vector spaces
• Vector spaces of finite and infinite dimensions
///////
Other relevant sources of information:
• Euclidean spaces
• Metric spaces
• Inner product spaces
• Vector spaces
• Normed vector spaces
• Normed vector spaces and inner product spaces
• Banach spaces
• The p-norm in finite dimensions
• {\ell}^p -spaces
• L^p -spaces
• L^{\infty} -spaces
• Hilbert spaces
• Orthonormal basis
• Dual basis
• Fourier series
• Fourier transform
///////
Spaces of countably infinite dimensions
(Sequence spaces and spaces of periodic functions)
Quoting Wikipedia (on Sequence spaces):
In functional analysis and related areas of mathematics, a sequence space is a vector space whose elements are infinite sequences of real or complex numbers. Equivalently, it is a function space whose elements are functions from the natural numbers to the field K of real or complex numbers. The set of all such functions is naturally identified with the set of all possible infinite sequences with elements in K, and can be turned into a vector space under the operations of pointwise addition of functions and pointwise scalar multiplication. All sequence spaces are linear subspaces of this space. Sequence spaces are typically equipped with a norm, or at least the structure of a topological vector space.
The most important sequence spaces in analysis are the \, ℓ^p spaces, consisting of the p-power summable sequences, with the p-norm. These are special cases of \, L^p \, spaces for the counting measure on the set of natural numbers. Other important classes of sequences like convergent sequences or null sequences form sequence spaces, respectively denoted \, c \, and \, c_0 , with the sup norm. Any sequence space can also be equipped with the topology of pointwise convergence, under which it becomes a special kind of Fréchet space called FK-space.
/////// End of quote from Wikipedia
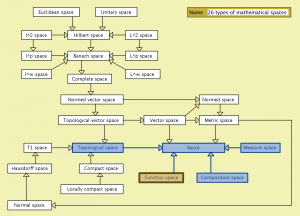
26 types of mathematical spaces:
Spaces of uncountably infinite dimensions
(Spaces of non-periodic functions)
///////