This page is a sub-page of our page on Geometric Algebra
///////
Sub-pages of this page:
• Origins of Geometric Algebra
///////
Related KMR-pages:
• Origins of Geometric Algebra
• Clifford Algebra
• Geometric Algebra
• Complex Numbers
• Quaternions
///////
Books:
• René Descartes (1637), La Géometrie
• Hermann Günther Graßmann (1844), Die Lineale Ausdehnungslehre, ein neuer Zweig der Mathematik
• A New Branch Of Mathematics – The Ausdehnungslehre of 1844 and Other Works, translated by Lloyd C. Kannenberg (1995)
• William Kingdon Clifford (1878), Applications of Grassmann’s Extensive Algebra, American Journal of Mathematics Vol. 1, No. 4 (1878), pp. 350-358 (9 pages), Published by: The Johns Hopkins University Press
• David Hestenes (1993, (1986)), New Foundations for Classical Mechanics
///////
Other relevant sources of information:
• Associative Composition Algebra (at Wikibooks)
• Quaternion (at Wikipedia)
• Rotor (at Wikipedia)
• Versor (at Wikipedia)
• Hyperbolic versor (at Wikipedia)
• Rotation formalisms in three dimensions (at Wikipedia)
• Elias Riedel Gårding (2017), Geometric algebra, conformal geometry and the common curves problem, Bachelors Thesis at the Royal Institute of Technology, Stockholm, Sweden
///////
The interactive simulations on this page can be navigated with the Free Viewer
of the Graphing Calculator.
///////
Anchors into the text below: ????????
„The World Health Organization has announced a world-wide epidemic of the Coordinate Virus in mathematics and physics courses at all grade levels. Students infected with the virus exhibit compulsive vector avoidance behavior, unable to conceive of a vector except as a list of numbers, and seizing every opportunity to replace vectors by coordinates. At least two thirds of physics graduate students are severely infected by the virus, and half of those may be permanently damaged so they will never recover. The most promising treatment is a strong dose of Geometric Algebra“. (Hestenes)
From the paper
Multiplication_of_vectors_and_structure_of_3D-Euclidean_space.pdf
by Miroslav Josipović, Zagreb, 2017.
A brief history of geometric algebra
The ancient greeks were in possession of the beginnings of a form of geometric algebra, namely the embryo of an exterior algebra. In terms of multiplication of units, it worked like this:
\, l_{ength} \times l_{ength} \equiv \, a_{rea} ,
\, l_{ength} \times l_{ength} \times l_{ength} \, \equiv \, v_{olume} ,
\, l_{ength} \times l_{ength} \times l_{ength} \times l_{enth} \equiv n_{othing} ,
since there were no more than three dimensions at that time. The idea of the existence of higher dimensions was hindered by a very powerful and concrete “reality block” that was impossible to overcome with the extremely clumsy and difficult-to-handle algebraic notation that the greeks had access to.
A fundamentally important contribution to removing this mental roadblock was provided by René Descartes in his book La Géometrie from 1637. As brilliantly described by David Hestenes in his book New Foundations for Classical Mechanics, Descartes introduced a cleverly chosen binary operation so that \, l_{ength} \times l_{ength} \, became equal to \, l_{ength} .
The person that threw open “the algebraic flood gates” to higher dimensions was a German high-school teacher in Stettin by the name of Hermann Günther Graßmann. In 1844 he published his masterpiece Die Lineale Ausdehnungslehre, ein neuer Zweig der Mathematik [A New Branch Of Mathematics – The Ausdehnungslehre of 1844 and Other Works, translated by Lloyd C. Kannenberg (1995)]. In English, this book is most often denoted by “Extension Theory” or “Theory of Extensions.”
In his Extension Theory – which nobody read at the time because it was written in an obscure philosophical style that no mathematicians were accustomed to – Graßmann introduced the idea of abstract vector spaces with n-dimensional algebra and geometry. In so doing, he created the domains of mathematics that we today refer to as linear algebra and exterior algebra (also known as multilinear algebra).
In 1878, William Kingdon Clifford, who tragically died the same year at the age of only 34, published the basics of an algebra, which today is called clifford algebra (but which he himself referred to as geometric algebra), and which builds upon the exterior algebra of Graßmann.
/////// Quoting Wikipedia on William Kingdon Clifford:
In 1878 Clifford published a seminal work, Applications of Grassmann’s extensive algebra, building on Grassmann’s algebraic work. He had succeeded in unifying the quaternions, developed by William Rowan Hamilton, with Grassmann’s outer product (also known as the exterior product). Clifford understood the geometric nature of Grassmann’s creation, and that the quaternions fit cleanly into the algebra Grassmann had developed. The versors in quaternions facilitate representation of rotation.
Clifford laid the foundation for a geometric product, composed of the sum of the inner product and Grassmann’s outer product. The geometric product was eventually formalized by the Hungarian mathematician Marcel Riesz. The inner product equips geometric algebra with a metric, fully incorporating distance and angle relationships for lines, planes, and volumes, while the outer product gives those planes and volumes vector-like properties, including a directional sensitivity.
Combining the two brought the operation of division into play. This greatly expanded our qualitative understanding of how objects interact in space. Crucially, it also provided the means for quantitatively calculating the spatial consequences of those interactions. The resulting geometric algebra, as Clifford called it, eventually realized the long sought goal[13] of creating an algebra that faithfully represents the movements and projections of objects in \, 3 -dimensional space.[14]
Moreover, Clifford’s algebraic schema extends to higher dimensions. The algebraic operations have the same symbolic form as they do in 2 or 3-dimensions. The importance of general Clifford algebras has grown over time, while their isomorphism classes – as real algebras – have been identified in other mathematical systems beyond simply the quaternions.
/////// End of quote from Wikipedia (on William Kingdon Clifford)
The definition of the geometric product
The geometric product of two vectors \, a \, and \, b \, is defined as the direct sum
of their inner product and their exterior product:
\, a \, b \stackrel {\mathrm{def}}{=} a \cdot b + a \wedge b .
By making use of the distributive property of the geometric product (see below), this definition can be extended to products of multivectors.
Terminology: Sums of products or products of sums (i.e., polynomials) of vectors from the same vector space are called multivectors.
Some properties of the geometric product
The geometric product of two vectors \, a \, and \, b \, “encodes” both their “degree of parallelity” and their “degree of orthogonality”:
Lemma 1: \, a \, b = a \cdot b \, if and only if the vectors are parallel.
Lemma 2: \, a \, b = a \wedge b \, if and only if the vectors are perpendicular.
Lemma 3: The inner product is symmetric: \, a \cdot b = b \cdot a ,
and the exterior product is antisymmetric: \, a \wedge b = - b \wedge a \, .
Therefore we have:
\, a \cdot b = \frac {1}{2} (a b + b a) , and
\, a \wedge b = \frac {1}{2} (a b - b a) .
Hence the geometric product of two vectors is naturally separated
into a symmetric and an antisymmetric part:
\, a \, b = \frac {1}{2} (a b + b a) + \frac {1}{2} (a b - b a) .
///////
The geometric product is associative, i.e., it satisfies \, (a \, b) \, c \, = \, a \, (b \, c) .
The geometric product is distributive over multivector addition (both from the left and from the right).
Let \, b = b_{ \, \shortparallel \, a} + b_{ \perp a} \, denote the splitting of the vector \, b \, into two components that are parallel respectively perpendicular to the vector \, a .
The distributivity from the left gives:
\, a \, b \, =
= \, a \, ( b_{ \, \shortparallel \, a} + b_{ \perp a} ) \, =
= \, a \, b_{\, \shortparallel \, a} \, + \, a \, b_{ \perp a} \, =
= \, a \cdot b_{\, \shortparallel \, a} + a \wedge b_{\, \shortparallel \, a} + a \cdot b_{ \perp a} + a \wedge b_{ \perp a} \, =
= \, a \cdot b_{\, \shortparallel \, a} + a \wedge b_{ \perp a} \, =
= \, a \cdot b + a \wedge b ,
as it should be.
With \, a = a_{ \, \shortparallel \, b} + a_{ \perp b} , the distributivity from the right gives:
\, a \, b \, =
= \, (a_{ \, \shortparallel \, b} + a_{ \perp b}) \, b \, =
= \, a_{ \, \shortparallel \, b} \, b + a_{ \perp b} \, b \, =
= \, a_{ \, \shortparallel \, b} \cdot b + a_{ \, \shortparallel \, b} \wedge b + a_{ \perp b} \cdot b + a_{ \perp b} \wedge b \, = \,
= \, a_{ \, \shortparallel \, b} \cdot b + a_{ \perp b} \wedge b \, =
= \, a \cdot b + a \wedge b ,
as it should be.
///////
SOME EXAMPLES OF WHAT A DIRECTED MAGNITUDE CAN ACHIEVE
///////
A directed line segment can point out an end point relative to a given start point
If the start point is regarded as the “zero-point” one gets a Euclidean vector which is a so-called direction vector. If the start point is included one gets an affine vector, also called a position vector.
///////
A directed planar area can solve the equation \, x^2 \, = \, -1 \, without the use of “imaginary” quantities
NOTE: The military solves the equation \, x^2 \, = \, -1 \, without the use of imaginary quantities. Here is how they do it:
\, { \text {left}}_{ \text {turn}} \; { \text {left}}_{ \text {turn}} \; {\text {start}}_{ \text {direction}} \, = \, { \text {left}}_{ \text {turn}}^2 \; {\text {start}}_{ \text {direction}} \, = \, { \text{half} }_{ \text {turn}} \; {\text {start}}_{ \text {direction}} \, = \, - \, {\text {start}}_{ \text {direction}} ,
\, { \text {right}}_{ \text {turn}} \; { \text {right}}_{ \text {turn}} \; {\text {start}}_{ \text {direction}} \, = \, { \text {right}}_{ \text {turn}}^2 \; {\text {start}}_{ \text {direction}} \, = \, { \text{half} }_{ \text {turn}} \; {\text {start}}_{ \text {direction}} \, = \, - \, {\text {start}}_{ \text {direction}} .
Hence the operations \, { \text {left}}_{ \text {turn}} \, and \, { \text {right}}_{ \text {turn}} \, perform the respective functions of the imaginary entities \, i \, and \, -i \, in the algebra of complex numbers.
In fact, we can easily introduce an infinite number of “imaginary units” in clifford algebra:
Let \, \mathcal {R} \, be a commutative ring with unit and let E be a finite, totally ordered set, i.e, E = \{e_1, \ldots, e_n\} where e_1 < e_2 < \ldots < e_n.
We define what is called \, k –base blades \, e_{n_1} e_{n_2} \ldots e_{n_k}, \, where \, n_1 < n_2 < \ldots < n_k \leq n, \, which we identify with the k -subsets \, \{e_{n_1}, \ldots, e_{n_k}\} \subseteq E. Moreover, we define the unit pseudoscalar \, e_1 e_2 \ldots e_n \, which we identify with the set \, E \, by an unproblematic change of context. Finally, we identify the ring unit \, 1 \, with the empty set \, \emptyset .
Then we have \, (e_i e_j)^2 = -1 \, as soon as \, i ≠ j. In fact, as is easily seen, the geometric product of any pair of perpendicular vectors of unit length is an imaginary unit, since it squares to \, -1 .
We regard the Clifford Algebra \, C_l(E) \, as the free \mathcal {R} -module genererated by the powerset \, \wp(E) \, of all subsets of \, E , i.e.,
\, C_l(E) \, = \, {\oplus \atop {e \, \in \, \wp(E) } } \mathcal {R} .
For the multiplication in \, C_l(E) \, we introduce, for the base elements, the following rules:
\, e_i^2 \, = \, 1 \, for \, i = 1, ..., n , and \; e_j \, e_i \, = \, - e_i \, e_j \, if \, i \neq j .
These “basic” rules are then extended distributively to all multivectors of \, C_l(E) .
A proof of the fact that these extended rules create a well-defined clifford algebra can be found in the appendix to the book-chapter:
• Naeve, A., Svensson, L. (2001): Geo-MAP unification, in Geometric Computing with Clifford Algebras – Theoretical Foundations and Applications in Computer Vision and Robotics, Sommer, G. (ed.), pp. 105-126, Springer Verlag, ISBN 3-540-41198-4.
If \, i \neq j \, we therefore obtain:
\,( e_i \, e_j)^2 \, = \, e_i \, e_j \, e_i \, e_j \, = \, - e_j \, e_i \, e_i \, e_j \, = \, - e_j \, e_j \, = \, -1 .
Hence, \, e_i \, e_j \, solves the equation \, x^2 \, = \, -1 . Each such bivector therefore functions as an imaginary unit.
///////
The complex numbers represented as the even subalgebra
of the clifford Algebra \, C_l(e_1, e_2) \, over the real numbers \, \mathbb{R} :
\, e_1, e_2 \, ,
\, e_1^2 = e_2^2 = 1 \, ,
\, e_2 e_1 = - e_1 e_2 \, .
Hence we have: \, (e_1 e_2)^2 = e_1 e_2 e_1 e_2 = - e_2 e_1 e_1 e_2 = - e_2 e_2 = -1 .
///////
Multiplying two 1-vectors in the Clifford algebra \, C_l(e_1, e_2) \, :
\, (\alpha_1 e_1 + \alpha_2 e_2) (\alpha'_1 e_1 + \alpha'_2 e_2) = \, = \alpha_1 e_1 \alpha'_1 e_1 + \alpha_1 e_1 \alpha'_2 e_2 + \alpha_2 e_2 \alpha'_1 e_1 + \alpha_2 e_2 \alpha'_2 e_2 \, = = \, \alpha_1 \alpha'_1 e_1 e_1 + \alpha_2 \alpha'_2 e_2 e_2 + \alpha_1 \alpha'_2 e_1 e_2 + \alpha_2 \alpha'_1 e_2 e_1 \, = = \, \alpha_1 \alpha'_1 + \alpha_2 \alpha'_2 + \alpha_1 \alpha'_2 e_1 e_2 - \alpha_2 \alpha'_1 e_1 e_2 \, == \, \alpha_1 \alpha'_1 + \alpha_2 \alpha'_2 + (\alpha_1 \alpha'_2 - \alpha_2 \alpha'_1) e_1 e_2 .
Multiplication in the even part of the Clifford algebra \, C_l(e_1, e_2) \, :
\, (x + y e_1 e_2) (x' + y' e_1 e_2) \, = = \, x x' + x y' e_1 e_2 + y e_1 e_2 x' + y e_1 e_2 y' e_1 e_2 \, = = \, x x' + x y' e_1 e_2 + y x' e_1 e_2 + y y' e_1 e_2 e_1 e_2 \, = = \, x x' + x y' e_1 e_2 + y x' e_1 e_2 - y y' e_2 e_1 e_1 e_2 \, == \, x x' - y y' + (x y' + y x') e_1 e_2 .
Multiplication in the algebra of complex numbers:
\, (x + iy ) (x' + iy') \, = = \, x x' + i x y' + i y x' + i^2 y y' \, == \, (x x' - y y') + i (x y' + y x') .
///////
A directed volume can liberate the Jacobi determinant from its surrounding modulus “straight jacket” when substituting variables in multiple integrals:
The dirty little secret of the multiple Riemann integral.
///////
The outer product can liberate the cross product from its 3-dimensional “straight jacket”
\, a \times b \, \stackrel {\mathrm{def}}{=} \, (a \wedge b) \, I^{-1} ,
where \, I = \, e_1 e_2 \cdots e_n \, is the unit pseudoscalar of \, C_l(e_1, e_2, \cdots, e_n) \, .
///////
Geometric operations can be carried out in a coordinate-free manner and have the same form in any dimension
Example:
The algebraic structure of a reflection in a hyperplane:
Let \, \pi \, be a hyperplane in \, {\mathbb{R}}^3 \, with the unit normal \, n .
NOTE: In the plane, a hyperplane is a 1D-line, and in 3D-space a hyperplane is a 2D-plane.
Theorem: A reflection \, S_{\pi} \, of the vector \, x \, in the hyperplane \, \pi \, with unit normal \, n \,
can be expressed as \, {\mathbb{R}}^3 \ni x \mapsto - \, n \, x \, n \, = \, \bar{x} = S_{\pi}(x) \in {\mathbb{R}}^3 .
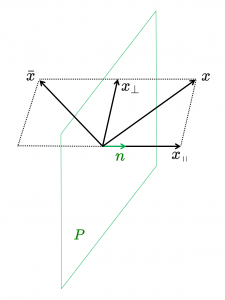
Proof: \, \bar{x} \, = \, - \, n \, x \, n \, = \, - \, n \, (x_{\, \shortparallel \, n} + x_{\perp n}) \, n \, = \, - \, n \, x_{\, \shortparallel \, n} \, n - \, n \, x_{\perp n} \, n \, = - \, n \, n \, x_{\, \shortparallel \, n} + n \, n \, x_{\perp n} \, = \, - \, x_{\, \shortparallel \, n} + x_{\perp n} \, = \, S_{\pi} (x) \, .∎
The interactive simulation that created this movie.
The blue vector \, x \, is reflected in the yellow plane \, \pi \, which contains the purple point \, P . The red vector \, n \, is the unit normal to the yellow plane \, \pi . The yellow vectors are the components of the blue vector that are parallel respectively orthogonal to the red vector \, n \, . The grey vector \, \bar{x} \, is the reflection of the vector \, x \, in the yellow plane \, \pi .
NOTE: For a unit normal \, n \, we have \, n \, n = n \cdot n = 1 . If the normal of the hyperplane does not have unit length, and since, for any non-zero vector \, v \, we have \, v^{-1} = \frac {1} {v} ,
we can adjust the reflection formula above by writing
\, S_{\pi} (x) \, = \, - \, n \, x \, n^{-1} .
///////
Reflection of a bivector in a hyperplane
///////
Rotations
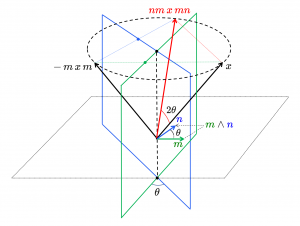
Two hyperplane reflections combine into a rotation around the hyperaxis of their intersection
Let the first respectively the second hyperplane of reflection have the normals \, m \, and \, n \, respectively (not necessarily of unit length). If we apply the hyperplane reflections first in \, m \, and then in \, n \, we get:
\, \bar {\bar{x}} \, = \, - \, n \, ( - \, m \, x \, m^{-1} ) \, n^{-1} \, = \, n \, m \, x \, m^{-1} n^{-1} \, = \, - n \, m \, x \, {(n \, m)}^{-1} \, = \, - R \, x \, R where \, R = n \, m .
The element \, R \, is called a versor.
///////
The algebraic and geometric structure of a versor:
/////// Quoting Wikibooks Associative Composition Algebra / Division quaternions:
Lemma 1: If \, a \, and \, b \, are square roots of minus one, and if \, a \perp b , we have \, a \, b \, a \, = \, b \, .
Proof: \,\; 0 \, = \, a \, (a \, b + b \, a) \, = \, a^2 \, b + a \, b \, a \, = \, -b + a \, b \, a \, .∎
Lemma 2: Under the same hypothesis we have \, a \perp a \, b \, and \, b \perp a \, b \, .
Proof: \, a \perp a\, b) \, : \, a \, (a \, b) + (a \, b) \, a \, = \, -b + a \, b \, a \, = \, 0 \, .∎
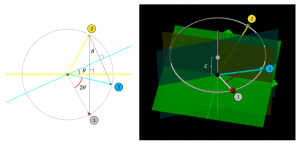
Let \, u = e^{\, \theta \, \mathbf{r}} \, be a versor. There is a group action on \, \mathbb{H} \, that is determined by \, u \, :
Inner automorphism \, f \, : \, \mathbb{H} \, \ni \, q \, \mapsto \, u^{-1} q \, u \, \in \, \mathbb{H} \, .
Note that \, u \, commutes with all vectors \, \{\, x + y \, \mathbf{r} \, : \, x, y \, \in \, \mathbb{R} \, \} .
Now choose \, \mathbf{s} \, from the great circle on \, \mathbb{S}^2 \, that is perpendicular to \, \mathbf{r} . Then, according lemma 1, we have \, \mathbf{r} \, \mathbf{s} \, \mathbf{r} \, = \, \mathbf{s} . Now compute \, f(\mathbf{s}) \, :
\;\;\;\;\;\;\;\;\;\;\;\; = \, ({\cos}^2 \theta - {\sin}^2 \theta) \, \mathbf{s} + (2\sin \theta \cos \theta) \, \mathbf{s} \, \mathbf{r} \, = \, \mathbf{s} \, \cos 2 \theta + \mathbf{s} \, \mathbf{r} \, \sin 2 \theta .
This represents a rotation with the angle \, 2 \theta \, in the \, (\mathbf{s}, \mathbf{s} \, \mathbf{r}) \, plane.
This property of \, \mathbb{H} , that there exists an inner automorphism \, f \, that produces rotations, has proved to be very useful.
/////// End of quote from Wikibooks
Two \, \theta -separated reflections produce a \, 2 \theta -separated rotation:
///////
The action of a fixed versor on a rotating vector:
The interactive simulation that created this movie
The film shows a red-tipped vector, the top of which rotates along the gray circle. Each position of this vector is reflected first in the horisontal yellow line (in the left window) with the corresponding reflection in the vertical yellow plane (in the right window). This action results in the yellow vector.
This vector is then reflected in the light-blue line (in the left window) with the corresponding reflection in the vertical light-blue plane (in the right window). This action results in the light-blue vector.
Since the light-blue vector is related to the red-tipped vector via a constant rotation, it follows that the light-blue vector follows the red-nosed vector at a constant distance and with a constant angle – around the circular cone whose axis of symmetry is identical to the \, z -axis.
///////
The action of a variable versor on a fixed vector:
The interactive simulation that created this movie
The variation of the versor is caused by a change in the angle between the yellow line and the light-blue line (in the left window) and hence the same change of the corresponding angle between the yellow vertical plane and the light-blue vertical plane (in the right window).
///////
The algebraic and geometric structure of a projection and rejection onto a blade
For any vector \, a \, and any invertible (i.e., non-zero) vector \, m \, we have,
\, a \, = \, a \, m \, m^{-1} \, = \, (a · m + a \wedge m) \, m^{-1} \, = \, a_{\, \shortparallel m} + a_{\, \perp m} ,
where the PROJECTION of \, a \, onto \, m \, (= the parallel part of \, a \, ) is
\, a_{\, \shortparallel \, m} \, = \, (a · m) m^{-1} ,
and the REJECTION of \, a \, from \, m \, (= the orthogonal part of \, a \, ) is
\, a_{ \perp m} \, = \, a - a_{\, \shortparallel \, m} \, = \, (a \wedge m) m^{-1} .
Using the facts that (1) a \, k -blade \, A \, is embedded in a k-dimensional subspace of \, V \, ,
and (2) that every multivector can be expressed in terms of vectors, this generalizes through linearity to general multivectors \, M . The projection is not linear in \, B \, and does not generalize to objects \, B \, that are not blades.
Projection of a general multivector \, M \, onto any invertible blade \, B :
\, {\text{Project}}_B(M) \, = \, M_{\, \shortparallel \, B} \, = \, (M ∟ B^{-1}) ∟ B ,
where ∟ denotes the left-inner product. The REJECTION of a general multivector \, M \, with respect to an invertible blade \, B \, is defined as
\, {\text{Reject}}_B(M) = M_{ \perp B} = M - M_{\, \shortparallel \, B} = M - (M ∟ B^{-1}) ∟ B .
The projection and rejection generalize to null blades \, B \, by replacing the inverse \, B^{-1} \, with the pseudoinverse \, B^p\, with respect to the contractive product. The outcome of the projection coincides in both cases for non-null blades. For null blades \, B , the definition of the projection given here with the first contraction rather than the second being onto the pseudoinverse should be used, as only then is the result necessarily true in the subspace represented by \, B .
/////// Quoting Gårding (2017, p. 18)
Theorem 2.10: (Proposition 3.2 in [1]). Every blade \, B = x_1 \wedge \cdots \wedge x_k \, can be written as a geometric product \, B = y_1 \, ... \, y_k \, where \, \{ y_1, \, ... \, ,y_k \} \, is an orthogonal set.
Proof: By Theorem A.2, there exists an orthogonal basis \, {b_1,...,b_k} \, for \, \bar{B} .
Writing \, x_i = \displaystyle\sum_{i=1}^j a_{ij}b_j , we find that \, B = λ b_1 \, ... \, b_k \, where \, λ \in R \, is some function of the \, a_{ij} \, (in fact, \, λ = \text{det}[a_{ij}] , as is argued in [1] by noting that \, λ \, is multilinear and alternating in the \, b_j ).∎
Corollary 2.10.1: If \, B \, is a blade, \, B^2 is a scalar.
Proof: By Theorem 2.10, write \, B \, as a geometric product \, B = y_1 \, ... \, y_k \, where the \, y_i \, are orthogonal to each other. Then, since \, y_i y_j = - y_j y_i \, if \, i ≠ j \, and the square of each \, y_i \, is a scalar, we have
\, y_1 \, ... \, y_k \, y_1 \, ... \, y_k \, = \,
\, = \, ± \, y_k \, ... \, y_2 \, {y_1}^2 \, y_2 \, ... \, y_k \, = \,
\, = \, ± \, {y_1}^2 \, y_k \, ... \, y_3 \, {y_2}^2 \, y_3 \, ... \, y_k \, = \,
\, = \, ± \, {y_1}^2 \, {y_2}^2 \, y_k \, ... \, y_3 \, y_3 \, ... \, y_k \, = \,
…
\, = \, ± \, {y_1}^2 \, {y_2}^2 \, {y_3}^2 \, ... \, {y_k}^2 \, ,
which is a scalar.∎
Remark: It can also be shown (though it is not as easy), that any multivector \, A \, with \, A^2 ∈ R \, must be a blade (see [1, Example 3.1 and Exercise 6.12]).
Corollary 2.10.2: Any blade \, B \, with \, B^2 ≠ 0 \, (a non-nullblade) is invertible with respect to the geometric product.
Proof: The inverse of \, B \, is \, B^{−1} = \dfrac {B} {B^2} .
/////// End of quote from Gårding
///////
\, \begin{bmatrix} \, x \, \\ \, y \, \\ \, z \, \end{bmatrix} \; \begin{bmatrix} -x \\ \; y \\ \; z \end{bmatrix} \; \begin{bmatrix} \; x \\ -y \\ \; z \end{bmatrix} \; \begin{bmatrix} \; x \\ \; y \\ -z \end{bmatrix} \; \begin{bmatrix} \; x \\ -y \\-z \end{bmatrix} \; \begin{bmatrix} -x \\ \; y \\ -z \end{bmatrix} \; \begin{bmatrix} -x \\ -y \\ \; z \end{bmatrix} \; \begin{bmatrix} -x \\ -y \\ -z \end{bmatrix}
///////
/////////////////////////////////////////////////////
Geometric numbers in Euclidean 3D-space:
\, R_{{eflect}\,i_{n}P_{lane}} (F_{orward}) \, \, R_{{eflect}\,i_{n}P_{lane}} (L_{eftward}) \, \, R_{{eflect}\,i_{n}P_{lane}} (U_{pward}) \,and the oppositely directed and equivalent reflection descriptions:
\, R_{{eflect}\,i_{n}P_{lane}} (B_{ackward}) \, = \, R_{{eflect}\,i_{n}P_{lane}} (F_{orward}) \, \, R_{{eflect}\,i_{n}P_{lane}} (R_{ightward}) \, = \, R_{{eflect}\,i_{n}P_{lane}} (L_{eftward}) \, \, R_{{eflect}\,i_{n}P_{lane}} (D_{ownward}) \, = \, R_{{eflect}\,i_{n}P_{lane}} (U_{pward}) \,///////
Dualisation:
\, (F_{orward} L_{eftward})^{\star} \, = \, (F_{orward} L_{eftward}) \, {(- \, F_{orward} L_{eftward} U_{pward})}^{-1} \, = \,
\, = \, - \, F_{orward} L_{eftward} (U_{pward})^{-1} (L_{eftward})^{-1} (F_{orward})^{-1} \, =
\, = \, - \, F_{orward} L_{eftward} D_{ownward} R_{ightward} B_{ackward} \, = \, F_{orward} L_{eftward} R_{ightward} D_{ownward} B_{ackward} \, =
\, = \, F_{orward} D_{ownward} B_{ackward} \, = \, - \, F_{orward} B_{ackward} D_{ownward} \, = \, - \, D_{ownward} \, = \, U_{pward}
\, (L_{eftward} U_{pward})^{\star} \, = \, (L_{eftward} U_{pward}) \, {(- F_{orward} L_{eftward} U_{pward})}^{-1} \, = \,
\, = \, - L_{eftward} U_{pward} (U_{pward})^{-1} (L_{eftward})^{-1} (F_{orward})^{-1} \, = \, - (F_{orward})^{-1} \, = \, - B_{ackward} \, = \, F_{orward}
\, (F_{orward} U_{pward})^{\star} \, = \, (F_{orward} U_{pward}) \, {(- \, F_{orward} L_{eftward} U_{pward})}^{-1} \, = \,
\, = \, - \, F_{orward} U_{pward} (U_{pward})^{-1} (L_{eftward})^{-1} (F_{orward})^{-1} \, =
\, = \, - \, F_{orward} R_{ightward} B_{ackward} \, = \, F_{orward} B_{ackward} R_{ightward} \, = \, R_{ightward} \, = \, - L_{eftward}
///////
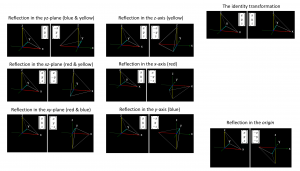
Reflections in planes, lines and points
Three reflections in perpendicular planes produce a reflection
in the point of intersection of the three planes (= the origin):
A reflection in a line is equal to a halfturn around this line:
\, R_{{eflect}\,i_{n}L_{ine}} (a_{line}) \, = \, R_{otate(H{alf}T_{urn})\,a_{round}} (t_{{he}L_{ine}}) \,Two reflections in perpendicular planes produce a halfturn around their line of intersection :
\, R_{{eflect}\,i_{n}P_{lane}} (F_{orward}) R_{{eflect}\,i_{n}P_{lane}} (L_{eftward}) \, = \, R_{{eflect}\,i_{n}L_{ine}} (L_{ine}(F_{orward} L_{eftward})^{\star}) \, = \, R_{otate(H{alf}T_{urn})\,a_{round}} (L_{ine} (U_{pward})) \, \, R_{{eflect}\,i_{n}P_{lane}} (L_{eftward}) R_{{eflect}\,i_{n}P_{lane}} (U_{pward}) \, = \, R_{{eflect}\,i_{n}L_{ine}} (L_{ine}(L_{eftward} U_{pward})^{\star}) \, = \, R_{otate(H{alf}T_{urn})\,a_{round}} (L_{ine} (F_{orward})) \, \, R_{{eflect}\,i_{n}P_{lane}} (F_{orward}) R_{{eflect}\,i_{n}P_{lane}} (U_{pward}) \, = \, R_{{eflect}\,i_{n}L_{ine}} (L_{inje}(F_{orward} U_{pward})^{\star}) \, = \, R_{otate(H{alf}T_{urn})\,a_{round}} (L_{ine} (R_{ightward})) \,Moreover we have the relations:
\, R_{{eflect}\,i_{n}P_{lane}} (F_{orward}) R_{{eflect}\,i_{n}P_{lane}} (F_{orward}) \, = \, 1 \, \, R_{{eflect}\,i_{n}P_{lane}} (L_{eftward}) R_{{eflect}\,i_{n}P_{lane}} (L_{eftward}) \, = \, 1 \, \, R_{{eflect}\,i_{n}P_{lane}} (U_{pward}) R_{{eflect}\,i_{n}P_{lane}} (U_{pward}) \, = \, 1 \,///////
Hyperbolic versors
/////// Quoting Wikipedia ( https://en.wikipedia.org/wiki/Versor#Hyperbolic_versor ):
A hyperbolic versor is a generalization of quaternionic versors to indefinite orthogonal groups, such as the Lorentz group. It is defined as a quantity of the form
\, \exp (a \, \mathbf{r}) \, = \, \cosh a + \mathbf{r} \, \sinh a \, , where \, | \, \mathbf{r} \, | \, = \, 1 \, .
Such elements arise in algebras of mixed signature, for example split-complex numbers or split-quaternions. It was the algebra of tessarines discovered by James Cockle in 1848 that first provided hyperbolic versors. In fact, James Cockle wrote the above equation (with \, \mathbf{j} \, in place of \, \mathbf{r} \, ) when he found that the tessarines included the new type of imaginary element.
This versor was used by Homersham Cox (1882/83) in relation to quaternion multiplication.[6][7] The primary exponent of hyperbolic versors was Alexander Macfarlane as he worked to shape quaternion theory to serve physical science.[8] He saw the modelling power of hyperbolic versors operating on the split-complex number plane, and in 1891 he introduced hyperbolic quaternions to extend the concept to 4-space. Problems in that algebra led to use of biquaternions after 1900. In a widely circulated review of 1899, Macfarlane said:
…the root of a quadratic equation may be versor in nature or scalar in nature. If it is versor in nature, then the part affected by the radical involves the axis perpendicular to the plane of reference, and this is so, whether the radical involves the square root of minus one or not. In the former case the versor is circular, in the latter hyperbolic.[9]
Today the concept of a one-parameter group subsumes the concepts of versor and hyperbolic versor as the terminology of Sophus Lie has replaced that of Hamilton and Macfarlane. In particular, for each \, \mathbf{r} \, such that \, \mathbf{r} \, \mathbf{r} = +1 \, or \, \mathbf{r} \, \mathbf{r} = -1 , the mapping \, a \, \mapsto \, \exp (a \, \mathbf{r}) \, takes the real line to a group of hyperbolic or ordinary versors. In the ordinary case, when \, \mathbf{r} \, and \, -\mathbf{r} \, are antipodes on a sphere, the one-parameter groups have the same points but are oppositely directed. In physics, this aspect of rotational symmetry is termed a doublet.
In 1911 Alfred Robb published his Optical Geometry of Motion in which he identified the parameter rapidity which specifies a change in frame of reference. This rapidity parameter corresponds to the real variable in a one-parameter group of hyperbolic versors. With the further development of special relativity the action of a hyperbolic versor came to be called a Lorentz boost.
/////// End of quote from Wikipedia (on hyperbolic versors)
///////
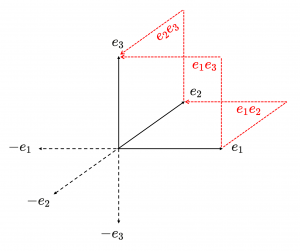
The quaternions as the even subalgebra
of the clifford algebra \, C_l(e_1, e_2, e_3) \, over the real numbers \, \mathbb{R} .
This diagram shows the 1-blades (unbroken black arrows) and the 2-blades (red, dotted, broken arrows) among the blades in the canonical basis for \, C_l(e_1, e_2, e_3) .
The negatives of the 1-blades are shown as dotted black arrows.
The 2-blades \, \textcolor {red} {e_1 e_2} \textcolor {black} {,} \textcolor {red} {e_2 e_3} \textcolor {black} {,} \textcolor {red} {e_1 e_3} \, , represent the directed area within the corresponding squares.
\, e_1^2 = e_2^2 = e_3^2 = 1 \, ,
\, e_k e_i = - e_i e_k , k \neq i \, .
Hence we have for \, k \neq i \, : \, (e_i e_k)^2 = e_i e_k e_i e_k = - e_k e_i e_i e_k = - e_k e_k = -1 .
Addition rule for the even subalgebra of \, C_l(e_1, e_2, e_3) \, :
\, (\alpha \textcolor {red} 1 + \alpha_{12} \textcolor {red} {e_1 e_2} + \alpha_{23} \textcolor {red} {e_2 e_3} \, + \alpha_{13} \textcolor {red} {e_1 e_3}) \, +
\, + \, (\alpha' \textcolor {red} 1 +\alpha'_{12} \textcolor {red} {e_1 e_2} + \alpha'_{23} \textcolor {red} {e_2 e_3} + \alpha'_{13} \textcolor {red} {e_1 e_3}) \stackrel {\mathrm{def}}{=} \,
\stackrel {\mathrm{def}}{=} \, (\alpha + \alpha') \textcolor {red} 1 + (\alpha_{12} + \alpha'_{12}) \textcolor {red} {e_1 e_2} + (\alpha_{23} + \alpha'_{23}) \textcolor {red} {e_2 e_3} + (\alpha_{13} + \alpha'_{13}) \textcolor {red} {e_1 e_3} .
Multiplication table for the even subalgebra of \, C_l(e_1, e_2, e_3) \, :
\, \begin{matrix} * & ~ & \textcolor {red} 1 & \textcolor {red} {e_1 e_2} & \textcolor {red} {e_2 e_3} & \textcolor {red} {e_1 e_3} \\ & & & & & & \\ \textcolor {red} 1 & ~ & \textcolor {red} 1 & \textcolor {red} {e_1 e_2} & \textcolor {red} {e_2 e_3} & \textcolor {red} {e_1 e_3} \\ \textcolor {red} {e_1 e_2} & ~ & \textcolor {red} {e_1 e_2} & - \textcolor {red} 1 & \textcolor {red} {e_1 e_3} & - \textcolor {red} {e_2 e_3} \\ \textcolor {red} {e_2 e_3} & ~ & \textcolor {red} {e_2 e_3} & - \textcolor {red} {e_1 e_3} & - \textcolor {red} 1 & \textcolor {red} {e_1 e_2} \\ \textcolor {red} {e_1 e_3} & ~ & \textcolor {red} {e_1 e_3} & \textcolor {red} {e_2 e_3} & - \textcolor {red} {e_1 e_2} & - \textcolor {red} 1 \, \end{matrix} \, .
Multiplication table for the quaternions:
\, \begin{matrix} * & ~ & \bold 1 & \;\; \bold i & \;\; \bold j & \, \;\, \bold k \\ & & & & & & \\ \bold 1 & ~ & \bold 1 & \;\; \bold i & \;\; \bold j & \;\; \bold k \\ \bold i & ~ & \bold i & - \bold 1 & \;\; \bold k & - \bold j \\ \bold j & ~ & \bold j & - \bold k & - \bold 1 & \;\; \bold i \\ \bold k & ~ & \bold k & \;\; \bold j & - \bold i & - \bold 1 \, \end{matrix} \,///////
Substituting \, \bold 1 = \textcolor {red} {1} \, , \, \bold i = \textcolor {red} {e_1 e_2} \, , \, \bold j = \textcolor {red} {e_2 e_3} \, , \bold k = \textcolor {red} {e_1 e_3} \, and comparing the two multiplication tables, we see that they are identical, and therefore they represent the same mathematical structure.
///////
What are quaternions, and how do you visualize them? A story of four dimensions.
(Steven Strogatz on YouTube):
/////// Quoting Wikipedia (on William Kingdon Clifford):
The realms of real analysis and complex analysis have been expanded through the algebra \, \mathbb {H} \, of quaternions, thanks to its notion of a three-dimensional sphere embedded in a four-dimensional space.
Quaternion versors, which inhabit this 3-sphere, provide a representation of the rotation group SO(3).
Clifford noted that Hamilton’s biquaternions were a tensor product \, \mathbb {H} ⊗ \mathbb {C} \, of known algebras, and proposed instead two other tensor products of \, \mathbb {H} :
Clifford argued that the “scalars” taken from the complex numbers \, \mathbb {C} \, might instead be taken from split-complex numbers \, \mathbb {S} \, or from the dual numbers \, \mathbb {D} \, . In terms of tensor products, \, \mathbb {H} ⊗ \mathbb {S} \, produces split-biquaternions, while \, \mathbb {H} ⊗ \mathbb {D} \, forms dual quaternions.
The algebra of dual quaternions is used to express screw displacement, a common mapping in kinematics.
/////// End of Quote from Wikipedia (on William Kingdon Clifford)