This page is a sub-page of the page on our Mathematical Explainatorium

///////

The sub-pages of this page are:

In Swedish:

• Siffrorna i våra liv: Hur vi använder matematik utan att räkna,
Stefan Buijsman, Natur & Kultur, 2019.

///////

Stefan Buijsman’s book “The digits in our lives” can be seen as a contribution to the discourse around the fascinating relations between mathematics and reality. In the three thematic chapters of the book (4, 5, and 6) that deal with respectively differential and integral calculus (ch. 4), probability theory and practice (ch. 5) and graph theory and practice (ch. 6) Buijsman engages with some of the underlying mathematical concepts almost entirely without formulas – with the single exception of a linguistic verson of Bayes formula in ch. 6.

I have great respect for Buijsman’s formula-free approach and I think his book has the potential to contribute to vitalizing the public discourse around what mathematics is and how it is applied in our daily lives, especially among young people.

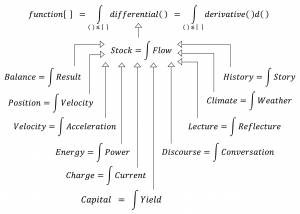
However, sometimes a purely textual approach leads to difficulties in clearly describing the properties of the mathematical concepts involved, which limits the understanding of their interactions. In Buijsman’s book this limitation is most clearly visible in his treatment of differential and integral calculus, where he avoids the fundamental theorem that states that differentiation and integration – when expressed properly – are inverse processes of each other. Unfortunately, in English, the verb “differentiate” does not mean “producing the differential” of a function – as one would expect – but rather “producing the derivative” of the function.

This linguistic incongruity makes it hard to carry out a more detailed discussion of the interaction of differentiation and integration. My page on Förändringsteori (= change theory) tries to throw some light on this situation – albeit in Swedish – and my page on Osäkerhetsteori (= uncertainty theory) tries to explain the connection between the concepts of integral and derivative in infinitesimal calculus, and their application counterparts, the concepts of distribution function and density function in probability theory.

Because of the many qualities present in Buijsmans formula-free descriptions of encounters with every-day mathematics that affect our lives in various ways, I have been inspired to embed his book in an “abstract space suit”, by which I mean a formula-based, and web-supported information layer “on top” of the book. This abstract layer has the potential to connect the formula-free stories to more traditional formula-based ones – mathematical stories that are “floating around” in abstract space – above the purely verbal ones.

To this aim I have made use of links to both Wikipedia and YouTube, and also to the Mathematical Explainatorium that has been created by the KMR-group at KTH over the past two decades. Hopefully, some of these formula-based stories could come under the scrutiny of some readers as a result of engaging with their verbal counterparts that are so vividly expressed in Buijsman’s book.

///////

A book connected with abstract mathematics through an abstract space suit:

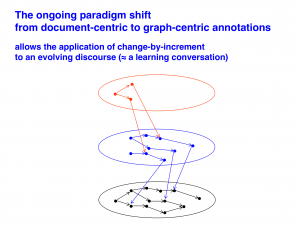
If you look at the space suit image you can see that there is a transformation going on in abstract space – from graph theory to category theory.

Overarching metaphor

Mathematics – like light – can exist and travel in vacuum. However, in the case of mathematics we are dealing with an abstract vacuum. Embedding books in abstract space suits helps them interface with this abstract mathematical vacuum

To many people abstraction seems to have a lot in common with “mental vacuum,” and therefore, abstractions are more or less unintelligible without a space suit that can connect with an inside level of “familiarity.”

///////

• Category Theory (at the KMR web site)
• The Linear War between the planets Vectoria and Vectoria’

///////

From document-centric to graph-centric annotations:

• The Universal Discourse (at the KMR web site)

///////

The fundamental theorem of calculus and some of its applications:

///////

Other candidate books for being fitted with abstract space suits
(with the common property of being physically present on my bookshelf):

In Swedish:

• Matte med mening: Tänka tal och söka mönster,
Kristin Dahl och Sven Nordqvist, ALFABETA Bokförlag, 1994.
• Fatta Matte – med kraftfull minnesträning,
Mattias Ribbing och Per Sundin, Månpocket och Forum, 2017.
• Att Finna Ett Spår – Erfarenheter ur waldorfpedagogiken,
Bengt Ulin, Robygge Bokhandel, Järna, 1982.
• Matematiken bakom allt: upptäck matten omkring dig, Colin Beveridge, Tukan förlag, 2018.
• Uträknad: Sanningen om algoritmerna som styr världen, David Sumpter, Volante, 2019.

In English:

• How to bake π: An Edible Exploration of the Mathematics of Mathematics,
Eugenia Cheng, Basic Books, 2015.
• Beyond Infinity – An expedition to the outer limits of the mathematical universe,
Eugenia Cheng, Profile Books, 2017.
• Are Numbers Real? – The uncanny relationships between math and the physical world,
Bryan Clegg, Robinson, 2016.
• Infinitesimal – How a Dangerous Mathematical Theory Shaped the Modern World,
Amir Alexander, One World Publishing, 2015.
• Zero – The Biography of a Dangerous Idea,
Charles Seife, Souvernir Press Ltd, 2000.
• Taming the Infinite – The story of mathematics from the first numbers to chaos theory,
Ian Stewart, Quercus, 2007.
• Seventeen Equations that Changed the World,
Ian Stewart, Profile Books, 2013.
• The Artist and the Mathematician – the story of Nicholas Bourbaki, the genius mathematician that never existed,
Amir D. Aczel, High Stakes Publishing, 2007.
• The Mystery of the Aleph – Mathematics, the Kabbalah, and the Search for Infinity,
Amir D. Aczel, Washington Square Press, 2000.
• Naming Infinity – a true story of religious mysticism and mathematical creativity,
Loren Graham and Jean-Michel Kantor, Harvard University Press, 2009.
• Unknown Quantity – A Real and Imaginary History of Algebra,
John Derbyshire, Atlantic Books, 2007.
• The Equation That Couldn’t Be Solved – How Mathematical Genius Discovered the Language of Symmetry, Mario Livio, Simon & Schuster, 2005.
• The Quantum Astrologer’s Handbook,
Michael Brooks, Scribe Publications, 2017.
• The Pythagorean Theorem – A Four Thousand Year History,
Eli Maor, Princeton University Press, 2007.
• e: The Story of a Number,
Eli Maor, Princeton University Press, 1994.
• Trigonometric Delights,
Eli Maor, Princeton University Press, 1994. 2002 (1998).
• The Story of The Square Root of -1 : An Imaginary Tale,
Paul J. Nahin, Princeton University Press, 1998.
• Street-Fighting Mathematics – The Art of Educated Guessing and Opportunistic Problem
Solving, Sanjoy Mahajan,The MIT Press, 2010.
• Weapons of Math Destruction: How Big Data Increases Inequality And Threatens
Democracy, Cathy O’Neil, Crown Publishing Group, 2016.
• How Not to Be Wrong – The Power of Mathematical Thinking,
Jordan Ellsberg, Penguin Books, 2015.
• Weird Math – At The Edge Of Infinity And Beyond,
David Darling and Agnito Banerjee, One World Books, 2018.
• Wonders Beyond Numbers: A Brief History Of All Things Mathematical,
Johnny Ball, Bloomsbury Sigma, 2019.

///////