This page is a sub-page of our page on Mathematical Concepts.
///////
The sub-pages of this page are:
///////
Related KMR-pages:
• Oscar Reutersvärd
• M.C. Escher
• Disambiguation
• Entropy
• Function
• Homology and Cohomology
• Homotopy
• Space
• Products
• Quotients
• Topos
• Duality
• Topology
• Uncertainty
• Dimension
///////
Other relevant sources of information:
• Modular arithmetic
• Gregorian calendar
///////
How big is your clock?
How many ticks does it take
to take it back
to where it started?
Different types of clocks: \, 7 \, , \{ 12, 2 \} \, , 24 \, , { \{ 28, 29, 30, 31 \} }^{12} \, , {\{ 365, 366 \}}^{ \, n \; ≥ \; 1583 } \,
…
hours, days, weeks, months, years, decades, centuries, millennia, …
Expanding the duration of each tick:
\, N_{days} \, = \, 7 \times N_{weeks} \,
\, N_{hours} \, = \, 24 \times N_{days} \,
\, N_{years} \, = \, 10 \times N_{decades} \,
\, N_{decades} \, = \, 10 \times N_{centuries} \,
\, N_{centuries} \, = \, 10 \times N_{millennia} \,
Modular arithmetic: \;\; x \, + \, n \times a \, \equiv \, x \pmod n \, \equiv \, x \pmod a \, , \forall \, x, n, a \in \mathrm Z.
What this formula means (in plain English) is that the integers \, x \, and \, x + n \times a \,
have the same remainder when you divide them by either the integer \, a \, or the integer \, n .
• Arithmetical crossfire
///////
Weekday calendar:
\, N_{days} \, = \, 7 \times N_{weeks} \,
\, \mathbb{Z} \, / \, 7\mathbb{Z} \, = \, {\mathbb{Z}}_7 \,
Question: What is the weekday a million days from now?
\, {10}^6 \pmod 7 \, \equiv \, 1 \, \in \, {\mathbb{Z}}_7 .
Answer: The same weekday as tomorrow.
///////
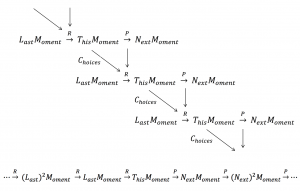
The shifting sequence of moments:
//////