Einstein for Flatlanders | Knowledge Management Research Group

This page is a sub-page of our page on Expandable Stories.

///////

Related KMR pages:

• Einstein for Linelanders
• Tesseracts for Flatlanders
• Stereographic Projection
• Hyperbolic Stereographic Projection
• Projective Geometry
• Projective Metrics
• The Euclidean Degeneration
• Metric Geometry
• Non-Euclidean Geometry
• Knowledge Negotiations

///////

Books:

• Flatland – A Romance Of Many Dimensions, by Edwin A. Abbott, 1884.
• Wolfgang Rindler (1966), Special Relativity, Oliver and Boyd, 1960.
• John Stillwell (1980), Classical Topology and Combinatorial Group Theory,
Springer Verlag, ISBN 0-387-90516-2.

///////

Other relevant sources of information:

• Minkowski spacetime
• Gravity visualized
• Lorentz transformations and symmetry
• The Poincaré Disk Model
• Hyperbolic Geometry within the Dynamics of Space and Time
• An artist’s theory on the physics of ‘Time’ as a physical process.Quantum Atom Theory.
• The speed of light is not about the speed of light (but about the speed of causality)
• Synthetic SpaceTime
• A Journey into the 4th Dimension – Perspective [Part 1]
• Visualizing 4D geometry. A Journey Into the 4th Dimension [Part 2]
• Flatland: The Movie – Official Trailer, 2007 film based on the novel Flatland
by Edwin A. Abbott from 1884.
• Flatland – the Limit of our Consciousness
• A Wrinkle In Time, 2018 Disney film based on the novel by Madeleine L’Engle from 1962.

///////

The interactive simulations on this page can be navigated with the Free Viewer
of the Graphing Calculator.

///////

Inertial Frames:

/////// Quoting Rindler (1966, p.4):

A frame of reference is a conventional standard of rest relative to which measurements can be made and experiments described. For example, if we choose a frame rigidly attached to the earth, the various points of the earth remain at rest in this frame while the “fixed” stars all trace out vast circles in the course of each day; if, on the other hand, we choose a frame attached to the fixed stars then these remain at rest while the points of the earth, other than on its axis, trace out approximate circles in the course of each day and the earth itself traces out an ellipse in the course of each year; and so on.

Among all possible frames there is one class which plays a special role in classical mechanics, namely the class of inertial (or Galilean) frames. These frames play an even more dominant role in the special theory of relativity and we must therefore define and discuss them carefully.

An inertial frame is one in which spatial relations, as determined by rigid scales at rest in the frame, are Euclidean and in which there exists a universal time in terms of which free particles remain at rest or continue to move with constant speed along straight lines (Newton’s first law).

Free particles placed without velocity at fixed points of an inertial frame will remain at those points, by definition. We can therefore picture an inertial frame as an aggregate of actual or virtual free test-particles mutually at rest, as determined by rigid scales. The distances between these “defining” particles satisfy the Euclidean axioms – an important stipulation in view of later developments. Straight lines in such a frame are defined as geodesics (lines of minimum length) and free particles not belonging to the defining aggregate move along such lines. We can further picture the defining particles as carrying the clocks whereby the progress of moving particles is timed.

By a “universal” time we mean a regular succession of frame-wide simultaneities in terms of which the laws of mechanics are homogeneous and isotropic (e.g., equal projectiles fired from equal guns anywhere and in any direction all move off with the same velocity). This is the classical concept of time, but we state it with reference to a given frame only. The time scale relative to which free particles are presumed to move uniformly in a given inertial frame may be called inertial time.

It is an open question whether time scales defined by various other identically repetitive processes, e.g., the vibrations of exited atoms, keep step over the centuries with inertial time; but in the idealized situation studied by special relativity we shall assume that they do. This is sometimes referred to as the homogeneity of time.

As we shall see, relativistic modifications do not affect Newton’s first law nor the existence of a universal time in this context, and the above classical definition of inertial frames is also that adopted in relativity. Although the full classical concept of a rigid body is untenable in relativity (see §12), the use we have made of “rigid scales” in the definition of inertial frames is also consistent with relativity; the term “resilient scales” would perhaps better describe our assumptions: such scales agree whenever they move uniformly side by side.

As in classical mechanics, it remains true in relativity that any two inertial frames must be in uniform translatory motion relative to each other (i.e., the defining particles of either frame move with equal constant speeds along parallel straight lines in the other frame) and, conversely, any frame in uniform translatory motion relative to an inertial frame is itself inertial. These statements will be proved in the next section.

Our definition of inertial frames is sufficiently complex to warrant the question whether such objects actually exist in nature. Since special relativity is largely concerned with propositions about inertial frames we want to be sure that the theory makes contact with reality.

We stress again that the existence of an inertial frame involves (i) the applicability of Euclidean geometry, (ii) the possibility of a certain definition of time throughout the frame, and (iii) the validity of Newton’s first law.

We shall now accept the existence of at least one inertial frame as an experimental fact: the frame of the “fixed” stars. But since all actual frames contain attracting masses which curve the paths of free test particles, in classical mechanics the strict definition is somewhat relaxed, and an inertial frame is defined as one in which free particles sufficiently far from all attracting masses follow straight paths, etc.

The implication is that if one were to remove those masses (e.g., the stars) one would be left with a strictly inertial frame; the presence of an overlay of gravitating matter in the frame is not considered to affect the rest of its physical properties, e.g., its Euclidean geometry and the existence of a universal time.

If, on the other hand, one adheres to the strict definition, one must accept the concomitant that inertial frames in nature can only be of limited extent, e.g., suitably chosen interstellar regions. In practice, of course, the physics postulated for such ideal frames is assumed to hold approximately also in some other frames, e.g., in the patently non-inertial terrestrial laboratory frame.

In this book all frames of reference considered will be inertial and all observers will be understood to use such frames (inertial observers). Sometimes the term “inertial” may be omitted, but it must always be understood.

The special principle of relativity:

Einstein’s reaction to the failure of all attempts to detect the ether frame was radical.
He advanced the following (special) principle of relativity:

A frame in uniform translatory motion relative to an inertial frame cannot be distinguished from that inertial frame by any physical experiment whatever.

It follows, in particular, that any such frame must itself be inertial. Conversely, any two inertial frames $\, S \,$ and $\, S' \,$ must be in uniform translatory motion relative to each other.

[…]

Thus, given the existence of a single inertial frame, it follows that there exists an infinite class of such frames containing, and only containing, all frames in uniform motion relative to the one whose existence is assumed. This being understood, Einstein’s principle can be restated as follows:

All inertial frames are equivalent for the formulation of all physical laws.

If, in this statement, we replace the phrase “all physical laws” by “all the laws of mechanics” we have a relativity principle which has been accepted ever since the days of Newton. Einstein’s innovation was to extend the principle from mechanics to the whole of physics. The very unity of physics strongly supports this step. For it has become increasingly obvious that physics cannot be separated into strictly independent branches. It would therefore be improbable that the laws of one branch of physics should transform differently from those of another branch.

But Einstein’s idea had such deep reprecussions on the concepts of space and time that, on closer examination, Newton’s laws of mechanics now turned out to be not strictly relativistic after all, and had to be modified (see chapter V).

There is an element of irony in the fact that the discipline which had always accepted a relativity principle should have to be amended in the light of the new relativity, whereas classical electro-magnetic theory, which so firmly committed itself to the existence of a preferred frame, should, in fact, come through unscathed (see chapter VI).

A first and immediate consequence of Einstein’s principle is the abolition of the ether concept. For suppose the ether frame could be detected. Then, whether or not this frame were inertial, we could by reference to it determine absolutely the motions of all other inertial frames. But this contradicts the relativity principle. Consequently the ether frame must remain undetectable, and in the realm of physics this is tantamount to being non-existent.

From now on, therefore, we must deny the existence of any one preferred frame and,
in particular, we must treat all inertial frames as completely equivalent.

/////// End of quote from Rindler (1966)

/////// Quoting Rindler (1966, p.10):

The Propagation of Light:

On the older hypothesis that light is a wave disturbance propagated through an all-pervaded static ether it was not difficult to be convinced of the validity of the following three propositions:

(i) light-signals are propagated rectilinearly through the ether with uniform velocity;
(ii) the velocity of propagation relative to the ether is independent of the velocity of the source;
(iii) the velocity of propagation relative to an observer travelling through the ether depends on the velocity of the observer.

In a simple corpuscular theory of light-propagation (ii) might have to be amended though (iii) is still “obvious”. Yet it is precisely (iii) that is overthrown by the relativity principle.

That light travels rectilinearly in vacuum in an inertial frame is indeed an old and well established experimental fact. (A priory it could curve, e.g., if made up of spinning particles reacting with an ether.) Its finite velocity was established by Roemer in 1675. That this velocity is independent of the velocity of the source was taken by Einstein in 1905 as an axiom, supported, like rectilinearity, by Maxwell’s theory.

De Sitter’s observation on double stars (1913) soon converted Einstein’s axiom into another experimental fact. Isotropy and spatial and temporal homogeneity then imply that the velocity of light is always the same. Compounded with relativity, this leads to the following law:

Light-signals in vacuo are propagated rectilinearly, with the same constant velocity $\, c \,$ at all times, in all directions, in all inertial frames.

Thus proposition (iii) above must be abandoned: no matter how we approach, or recede from, a light-signal, it always has the same constant velocity relative to us, provided, of course, we move uniformly relative to the inertial frames. (In the sequel such a motion will simply be called uniform.)

At first this is very hard to to visualize. No simple undulatory or corpuscular theory provides a model for this kind of propagation in classical space and time. But it was part of Einstein’s genius to realize that our classical concepts of space and time were dispensable.

We have now developed the two propositions on which the whole of special relativity is based: the relativity principle and the law of light-propagation. As we have seen, the latter is not entirely independent of the former. Its independent and significant core is the existence in one inertial frame of some effect that is propagated rectilinearly through empty space with a finite, source-independent velocity.

The essence of the law of light-propagation is thus a physical fact, susceptible of experimental verification. Einstein’s theory was touched off by applying the principle of relativity to the basic fact of light-propagation.

/////// End of quote from Rindler (1966).

The Lorentz transformation:

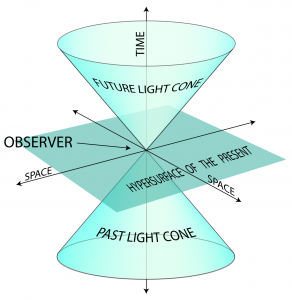
The four parts of Minkowski spacetime (from Wikipedia):

/////// Quoting Rindler (1966, p.21):

The Lorentz equations as a transformation from $\, (x, y, z, t) \,$ to $\, (x', y', z', t') \,$ :

$\; x' = \frac{ x \, - \, v t} {{(1 \, - \, v^2/c^2)}^{1/2}} \; ,$ $\; y' = y \; ,$ $\; z' = z \; ,$ $\; t' = \frac{t \, - \, v x/c^2} {{(1 \, - \, v^2/c^2)}^{1/2}} \; . \; \; \; \; \; \; \; \; \; \; \; \; (1.10)$

The inverse transformation from $\, (x', y', z', t') \,$ to $\, (x, y, z, t) \,$ :

$\; x = \frac{ x' \, + \, v t} {{(1 \, - \, v^2/c^2)}^{1/2}} \; ,$ $\; y = y' \; ,$ $\; z = z' \; ,$ $\; t = \frac{t' \, + \, v x'/c^2} {{(1 \, - \, v^2/c^2)}^{1/2}} \; . \; \; \; \; \; \; \; \; \; \; \; \; (1.11)$

The Lorentz transformations are non-singular (their determinant is easily seen to be unity) and they possess the two so called group properties.

Algebraic solution of (1.10) for $\, (x, y, z, t) \,$ gives (1.11). Hence the inverse of a Lorentz transformation with parameter $\, v \,$ is a Lorentz transformation with parameter $\, -v .$

Moreover, the resultant of two successive Lorentz transformations with parameters $\, v_1 \,$ and $\, v_2 \,$ respectively, is also found to be of type (1.10) with parameter

$\, v = \frac{v_1+v_2}{1+v_1 v_2/c^2} \,$ .

We note, finally, that any effect whose speed of propagation in vacuo is finite and constant could have been used, as light was, in the derivation of the Lorentz equations. Since only one transformation can be valid, it follows that all such effects must be propagated by the speed of light. Examples are provided by electro-magnetic waves of all frequencies.

/////// End of quote from Rindler (1966)

• Electromagnetic radiation

A planar electromagnetic wave:

The interactive simulation that created this movie.

The electric part of the wave: $\, E(\mathbf{\hat{k}}, \mathbf{x}, \omega, t) \, = \, e^{ \, i \,(\mathbf{\hat{k}} \cdot \mathbf{x} \, - \, \omega \, t)} \,$

The magnetic part of the wave: $\, B(\mathbf{\hat{k}}, \mathbf{x}, \omega, t) \, = \, e^{ \, i \, (\mathbf{\hat{k}} \cdot \mathbf{x} \, - \, (\omega \, + \, \pi/2) \, t)} \,$

The entire wave: $\, E_m(\mathbf{\hat{k}}, \mathbf{x}, \omega, t) \, = \, E(\mathbf{\hat{k}}, \mathbf{x}, \omega, t) \, + \, B(\mathbf{\hat{k}}, \mathbf{x}, \omega, t) \,$

Its Poynting vector : $\, S \, = \, \frac{1}{{\mu}_0} \, E \, \times \, B$

///////

Lorentz transformation Flatland::Elsewhere:

The Lorentz transformation of “special relativity for flatlanders” (= 2-dimensional beings). The purple event is observed from the blue respectively the red inertial frames, which are moving uniformly relative to each other.

These observations are represented by the blue respectively the red points in Minkowski spacetime (= the window to the right). The light cone is given by the yellow surface.

Both observations are located on the one-sheeted hyperboloid (= the gray surface).

Both observers therefore agree that the purple event occured “elsewhere”.

You can download the interactive (graphing calculator) file from here.

Scrolling to the bottom of the algebra window you will find the parameter $\, b \,$ which controls the time (seen from the blue frame) of the appearance of the purple event, and the parameter $\, V \,$ , which controls the relative speed of the two frames.

By varying the parameter $\, V \,$ you can observe how the red point (in the Minkowski window) moves along the gray surface, and by varying the parameter $\, b \,$ you can watch the gray surface change its shape.

///////

Lorentz transformation Flatland::Future:

In this case, both observations are located on the “future sheet” of the two-sheeted hyperboloid (= the gray surface).

Both observers therefore agree that the purple event occured “in the future”.

///////

You can download the interactive (graphing calculator) file from here.

///////

Lorentz transformation Flatland::Past:

In this case, both observations are located on the “past sheet” of the two-sheeted hyperboloid (= the gray surface).

Both observers therefore agree that the purple event occurred “in the past”.

///////

You can download the interactive (graphing calculator) file from here.

/////// Quoting Rindler (1966, p.25):

Relativistic Kinematics:

We first introduce a standard notation. The Lorentz factor will be denoted by the symbol $\; \gamma \;$ , or, occationally by $\; \gamma(v) \,$ . Hence we have

\; \gamma \equiv \gamma(v) \equiv {(1 - v^2/c^2)}^{-1/2} \;

The Lorentz transformation equations can now be written

\; x' \equiv \gamma (x - vt) \; , y' \equiv y \; , z' \equiv z \; , t' \equiv \gamma (t - vx/c^2) \; , \; \; \; \; \; \; \; \; \; \; \; (2.3)

and

\; x \equiv \gamma (x' + vt') \; , y \equiv y' \; , z \equiv z' \; , t \equiv \gamma (t' + vx'/c^2) \; . \; \; \; \; \; \; \; \; \; \; (2.4)

/////// End of quote from Rindler (1966)

/////// Quoting Rindler (1966, p. 34):

Transformation of velocities:

$\; u_1 = \frac{dx}{dt} \; , \; u_2 = \frac{dy}{dt} \; , \; u_3 = \frac{dz}{dt} \; , \; \; \; \; \; \; \; \; \; \; \; \; \;\; \; \; \; \; (2.7)$ ,

and, similarly,

\; u'_1 = \frac{dx'}{dt'} \; , \; u'_2 = \frac{dy'}{dt'} \; , \; u'_3 = \frac{dz'}{dt'} \; . \;\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; (2.8)

Now we can write (2.3) in differential form as

\; dx' \equiv \gamma (dx - v dt) \; , dy' \equiv dy \; , dz' \equiv dz \; , dt' \equiv \gamma (dt - v dx/c^2) \; \; \; \; \; \; \; (2.9)

If we substitute these differentials in (2.8) and use (2.7), we obtain the desired transformation formulae,

\; u'_1 \equiv \frac{u_1 - v}{1-u_1 v/c^2} \; , u'_2 \equiv \frac{u_2}{\gamma(1 - u_1 v/c^2)} \; , u'_3 \equiv \frac{u_3}{\gamma(1 - u_1 v/c^2)} \; . \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; (2.10)

As in the transformation of the coordinates, we can pass to the inverse relations by interchanging primed and unprimed symbols and at the same time writing $\, -v \,$ for $\, v \,$ . This is the standard procedure for obtaining inverses of transformations relating quantities in $\, S \,$ and $\, S' \,$ . Thus

\; u_1 \equiv \frac{u'_1 + v}{1 + u'_1 v/c^2} \; , u_2 \equiv \frac{u'_2}{\gamma(1 + u'_1 v/c^2)} \; , u_3 \equiv \frac{u'_3}{\gamma(1 + u'_1 v/c^2)} \; . \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; (2.11)

These equations also result, naturally, from direct solution of (2.10).

The relativistic formulae (2.10) and (2.11) differ from the corresponding classical formulae by the presence of the denominators. The classical formulae can be recovered, as might be expected, by letting $\, c \rightarrow \infty$ . Note that even the transversal velocity components generally differ in the two frames.

[…]

A straightforward computation yields from (2.11) the following relation between the magnitudes $\, u \equiv {({u_1}^2+{u_2}^2+{u_3}^2)}^{1/2} \,$ and $\, u' \equiv {({u'_1}^2+{u'_2}^2+{u'_3}^2)}^{1/2} \,$ of the velocities:

\, c^2 - u^2 = \frac{c^2 (c^2 - u'^2) (c^2 - v^2)} {(c^2 + u'_1 v)^2} \, . \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \;\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; (2.12)

If $\, u' < c \,$ and $\, v < c \,$ the right member is positive, whence $\, u < c \,$ . In other words, the resultant of two velocities less than $\, c \,$ is itself a velocity less than $\, c \,$ . We see further from (2.12) that either $\, u' = c \,$ or $\, v = c \,$ implies $\, u = c \,$ , i.e. that the “addition” of any velocity to the velocity of light yields again the velocity of light. This merely recovers our starting point, namely that the velocity of light is the same for all observers. Velocities measured in the same frame are, of course compounded as in the classical theory according to the usual vector rule. Thus the relative velocity of two particles as measured in a frame in which both move can be as much as $\, 2c \,$ .

/////// End of quote from Rindler (1966).

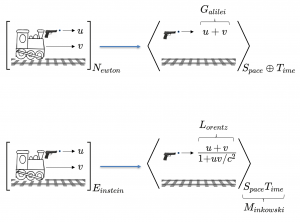
\; u + v \;

\; N_{ewton} = S_{pace} \oplus T_{ime} \;

\; E_{instein} = S_{pace}T_{ime} \;

\; M_{inkowski} \; L_{orentz} \; G_{alilei} \;

\; \frac{u + v} {1 + u v/c^2} \;

///////

• Mathematics is Representation

///////

Newton and Einstein firing a bullet along the track of a running train
and computing its velocity with respect to the ground:

$\; {\lbrack v_{elocity}(b_{ullet}) \rbrack}_{t_{rain}} = u \;$ , and
$\; {\lbrack v_{elocity}(t_{rain}) \rbrack}_{t_{rack}} = v \;$ ,

and we want to find

$\; {\lbrack v_{elocity}(b_{ullet}) \rbrack}_{t_{rack}} \;$ .

Newton’s theory now gives:

$\; {\lbrack {\lbrack v_{elocity}(b_{ullet}) \rbrack}_{t_{rack}} \rbrack}_{N_{ewton}} = {\langle u + v \rangle}_{N_{ewton}} \;$ ,

while Einstein’s theory gives:

$\; {\lbrack {\lbrack v_{elocity}(b_{ullet}) \rbrack}_{t_{rack}} \rbrack}_{E_{instein}} = {\langle \frac{u + v} {1 + u v/c^2} \rangle}_{E_{instein}} \;$ .

///////

Hyperbolic Geometry: The Riemann-Poincaré disc model of the hyperbolic plane

The Poincaré model (vary a) (MathRehab on YouTube):

///////

Devil moving rigidly in the Riemann-Poincaré disc:

///////

Poincaré strikes back (at Escher)
Angels and Devils moving in the Poincaré disc:

///////

The Beltrami-Klein model (vary a)
(MathRehab on YouTube):

///////

Central projection of spherical circles onto the tangent plane at the south pole
(MathRehab on YouTube)

///////

Hyperbolic Geometry is Projective Relativistic Geometry
(full lecture by N.J. Wildberger):

///////

Wild Linear Algebra 34: Oriented circles and 3D relativistic geometry I:

///////

Wild Linear Algebra 35: Oriented circles and 3D relativistic geometry II:

///////

Universal Hyperbolic Geometry 1: Apollonius and polarity (by N.J. Wildberger):

///////

Nature of time and simultaneity
(Eugene Khutoryansky on YouTube):

///////

Einstein’s Relativistic Train in a Tunnel Paradox:
Special Relativity (Eugene Khutoryansky on YouTube):

///////

The big ideas of physics:

Einstein’s general theory of relativity

///////

The Speed of Light is NOT About Light
(Space Time | PBS Digital Studios on YouTube):

///////

Flatland – the movie:

///////

Flatland – the limit of our consciousness:

///////

Flatland The Movie – Tony Hale as King of Pointland:

///////

Flatland: Reflections:

///////

Moebius Story: Wind and Mr. Ug::

///////

Moebius highway:

///////

The Klein bottle:

///////

Cyclist on a Klein bottle:

///////

The adventures of the Klein bottle:

///////

HyperSpace

Sphereland – Teaser Trailer:

///////

Hypersphere 2:

///////

Hypersphere 4:

///////

The 4th dimension explained (Carl Sagan on YouTube):

///////

Understanding 4D — The Tesseract (LeiosOS on YouTube):

///////

Tesseracts for Flatlanders
The HyperSquare (= “Triact”) that explains the HyperCube (= “Tesseract”):

///////

This video shows:

The 3Cube as a HyperSquare (= Triact) casting its shadow onto Flatland (= 2Space).

A rotating 3Cube can be projected onto 2Space from a 3Point outside of this 2Space, which produces the “inside-out” turning motions of its shadows in 2Space.

Interactive simulation of the projection onto 2Space of a rotating 3Cube.

Correspondingly we can regard:
The 4Cube as a HyperCube (= Tesseract) casting its shadow onto Space (= 3Space).

A rotating 4Cube can be projected onto 3Space from a 4Point outside of this 3Space, which produces the “inside-out” turning motions of its shadows in 3Space.

///////

Unwrapping a tesseract (4d cube aka hypercube):

(Vladimir Panfilov on YouTube)

///////

Interactive simulation of the projection onto 3Space of a rotating 4Cube (by Ron Avitzur).

In this simulation the four orthogonal directions of 4Space are given by x, y, u, v. The 4Cube can be interactively rotated around the xy-, xu-, xv-, yu-, yv-, and uv-planes. In 4D, the axis (= invariant subspace) of a rotation is a 2Space (= a plane).

///////

Tesseract – 6 rotations: