Adjoint Functors | Knowledge Management Research Group

This page is a sub-page of our page on Category Theory.

///////

Related KMR pages:

/////// Quoting from (Spivak, 2014, p. 383):

1.1. Quantifiers as adjoints

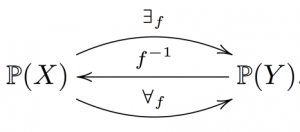
One of the simplest but neatest places that adjoints show up is between preimages and the logical quantifiers $\, \exists \,$ and $\, \forall$ , which we first discussed in Notation 2.1.1.1. The setting in which to discuss this is that of sets and their power preorders. That is, if $\, X \,$ is a set then recall from Section 4.4.2 that the power set $\, \mathbb{P}(X) \,$ has a natural ordering by inclusion of subsets.

Given a function $\, f : X \rightarrow Y \,$ and a subset $\, V \subseteq Y \,$ the preimage of $\, V \,$ is

$\,\,\,\,\,\,\,\, f^{-1}(V) \coloneqq \{ x \in X \, | \, f(x) \in V \}$ .

If $\, V' \subseteq V \,$ then $\, f^{-1}(V') \subseteq f^{-1}(V) \,$ , so in fact $\, f^{-1} : \mathbb{P}(Y) \rightarrow \mathbb{P}(X) \,$ can be considered a functor (where of course we are thinking of preorders as categories). The quantifiers $\, \exists \,$ and $\, \forall$ appear as adjoints of $\, f^{-1}$ .

Let’s begin with the left adjoint of $\, f^{-1} : \mathbb{P}(Y) \rightarrow \mathbb{P}(X)$ . It is a functor $\, L_f : \mathbb{P}(X) \rightarrow \mathbb{P}(Y)$ . Choose an object $\, U \subseteq X \,$ in $\, \mathbb{P}(X)$ . It turns out that

$\, L_f(U) \coloneqq \{ y \in Y \, | \, \exists x \in f^{-1}(y) \,$ such that $\, x\in U \}$ .

And the right adjoint $\, R_f : \mathbb{P}(X) \rightarrow \mathbb{P}(Y)$ , when applied to $\, U$ , is

$\, R_f(U) \coloneqq \{ y \in Y \, | \, \forall x \in f^{-1}(y) \, , \, x \in U \}$ .

In fact, the functor $\, L_f \,$ is generally denoted $\, {\exists}_f : \mathbb{P}(X) \rightarrow \mathbb{P}(Y)$ ,
and the functor $\, R_f \,$ is generally denoted $\, {\forall}_f : \mathbb{P}(X) \rightarrow \mathbb{P}(Y)$ .

The following example shows why this notation is apt.

1.1.1. Example 7.1.1.13.
In logic or computer science, the quantifiers $\, \exists \,$ and $\, \forall$ are used to ask whether any or all elements of a set have a certain property. For example, one may have a set of natural numbers and want to know whether any or all are even or odd.

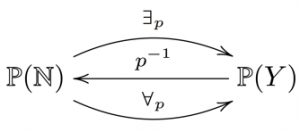
Let $\, Y = \{ \mathrm{even}, \mathrm{odd} \}$ , and let

\, p : \mathbb{N} \rightarrow Y \,

be the function that assigns to each natural number its parity (even or odd). Because the elements of $\, \mathbb{P}(\mathbb{N}) \,$ and $\, \mathbb{P}(Y) \,$ are ordered by inclusion of subsets, we can construe these orders as categories (by Proposition 5.2.1.13). What is new is that we have adjunctions between these categories

Given a subset $\, U \subseteq \mathbb{N}$ , i.e., an object $\, U \in \mathrm{Ob}(\mathbb{P}(\mathbb{N}))$ , we investigate the objects $\, {\exists}_p(U) \,$ and $\, {\forall}_p(U)$ . These are both subsets of $\, \{\mathrm{even}, \mathrm{odd}\}$ . The set $\, {\exists}_p(U) \,$ includes the element $\, \mathrm{even} \,$ if there exists an even number in $\, U$ ; it includes the element $\, \mathrm{odd} \,$ if there exists an odd number in $\, U$ . Similarly, the set $\, {\forall}_p(U) \,$ includes the element $\, \mathrm{even} \,$ if every even number is in $\, U \,$ and it includes $\, \mathrm{odd} \,$ if every odd number is in $\, U$ .

Let’s use the definition of adjunction to ask whether every element of $\, U \subseteq \mathbb{N} \,$ is even. Let $\, V = \{\mathrm{even}\} \subseteq Y$ . Then $\, f^{-1}(V) \subseteq \mathbb{N}$ is the set of even numbers, and there is a morphism $\, U \rightarrow f^{-1}(V) \,$ in the preorder $\, \mathbb{P}(\mathbb{N}) \,$ if and only if every element of $\, U \,$ is even. Therefore, the adjunction isomorphism

\,\,\,\,\,\,\,\, {\mathrm{Hom}}_{ \, \mathbb{P}(\mathbb{N})}(U, f^{-1}(V)) \simeq {\mathrm{Hom}}_{ \, \mathbb{P}(Y)}({\exists}_p(U), V) \,

says that $\, {\exists}_p(U) \subseteq \{\mathrm{even}\} \,$ if and only if every element of $\, U \,$ is even.

NOTE: It may not be clear that by this point we have also handled the question, “is every element of $\, U \,$ even?” One simply checks that $\, \mathrm{odd} \,$ is not an element of $\, {\exists}_p(U)$ .

/////// End of Quote from (Spivak, 2014)

///////

\, \langle \, \Sigma \, F \, , \, G \, \rangle \, \simeq \, \langle \, F \, , \, \Delta \, G \, \rangle \,

\, \langle \, \Delta \, F \, , \, G \, \rangle \, \simeq \, \langle \, F \, , \, \Pi \, G \, \rangle \,

///////

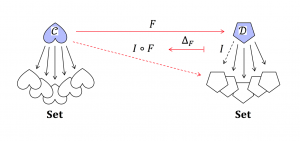
A Schema Mapping $\, F \,$ and its corresponding Pullback Functor $\, { \triangle }_F \,$ :

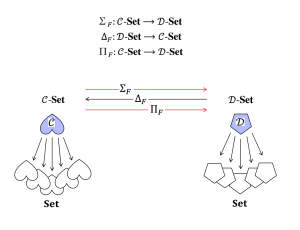
Left and Right Adjoints of the Schema Pullback Functor:

$I \coloneqq \{ \, i \, | \, i \; \text{is an} \, I_{nstitution} \} \,$ .

The set of schemas used by the institution $\, i \,$ :

\, S(i) \coloneqq \{ \, S_k(i) \, | \, S_k(i) \; \text{is a schema used by the} \, I_{nstitution} \, i \, \}

\, V(S_k(i)) \coloneqq \{ \, v(S_k(i)) \, | \, v(S_k(i)) \, \text{is a table in} \, S_k(i) \, \} \cong \{ \, \text{primary keys in} \, S_k(i) \, \}

\, A(S_k(i)) \coloneqq \{ \, a(S_k(i)) \, | \, a(S_k(i)) \, \text{is an arrow in} \, S_k(i) \, \} \cong \{ \, \text{foreign keys in} \, S_k(i) \, \}

$\, G(S_k(i)) \coloneqq \,$ the graph of $\, S_k(i)$ , i.e., $\, S_k(i) \equiv (G(S_k(i)), \simeq)$ .

Hence we can write:

$\, G(S_k(i)) = ( \, V(S_k(i)) \, , A(S_k(i)) \, , \, s_{rc} : \, A \rightarrow V \, , \, t_{gt} : \, A \rightarrow V \, ) \,$ .

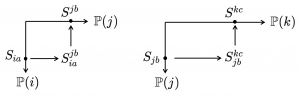
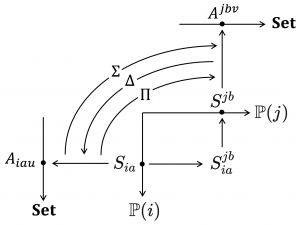
Let $\, \mathbb{P}(i) \coloneqq 2^{ \, S(i)} = \{ \, P(i) \, | \, P(i) \subseteq S(i) \, \} \,$ and let $\, S_{ia} \in \mathbb{P}(i) \,$ and $\, S_{jb} \in \mathbb{P}(j) \,$ , where $\, a \,$ is indexing $\, \mathbb{P}(i) \,$ and $\, b \,$ is indexing $\, \mathbb{P}(j)$ .

Moreover, let

$\, A_{ia} \coloneqq \, \{ \,$ annotations $\, A_{iau} \, | \, A_{iau} \,$ makes use of $\, S_{ia} \,$ within the context $\, u \, \} \,$ , and

$\, A_{jb} \coloneqq \, \{ \,$ annotations $\, A_{jbv} \, | \, A_{jbv} \,$ makes use of $\, S_{jb} \,$ within the context $\, v \, \} \,$ .

Define the category $\, \mathbb{C}(i) \,$ by:

1) $\, O_{bj}( \, \mathbb{C}(i) \, ) \coloneqq {\bigcup \limits_{i \in I}^{ \text {} }} \, \mathbb{P}(i) \,$ .

2) For each pair of objects $( \, \mathbb{P}(i) \, , \, \mathbb{P}(j) \, ) \in O_{bj}( \, \mathbb{C}(i) \, ) \,$

Define $\, {\hom}_{ \, \mathbb{C}(i)}( \, \mathbb{P}(i) \, , \, \mathbb{P}(j) \, ) \,$ as the $\, |\mathbb{P}(i)|\times|\mathbb{P}(j)| \,$ matrix $\, S_{ia} \, S^{jb} \eqqcolon S_{ia}^{jb} \,$ .

We then have:

$\, S_{ia}^{jb} = \{ \,$ schema mappings $\, S_{ia}^{jb}(q) \, | \, S_{ia}^{jb}(q) \,$ relates $\, S_{ia} \,$ to $\, S_{jb} \,$ in the context $\, q \, \}$ .

Since $\, S_{ia}^{kc} = S_{ia}^{jb} S_{jb}^{kc} \,$ the arrows in $\, \mathbb{C}(i) \,$ can be concatenated, and since matrix multiplication is associative, so is the arrow concatenation. Hence $\, \mathbb{C}(i) \,$ fulfills the requirements on a category.

///////

\, S^{kc} \, \mathbb{P}(k) \,

///////////////////////////// Infrastructures for cross-institutional reasoning p. XXX

ADJOINT FUNCTORS

50. Adjoint functors

50.1. Introduction

50.2. Discussion and definition

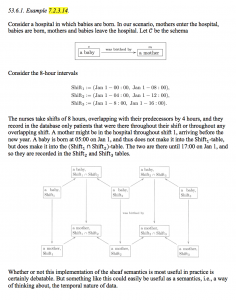
(cont.)

50.3. The analogy continued

50.4. Isomorphism of adjoints

50.5. Example

50.6. Some more examples of adjuctions

50.7. Quantifiers as adjoints

(cont.)
Example

50.8. Universal concepts in terms of adjoints

(cont.1)

(cont.2)

50.9. Preservation of colimits or limits

51. DATA MIGRATION

51.1. Pullback: ∆

(cont.1)

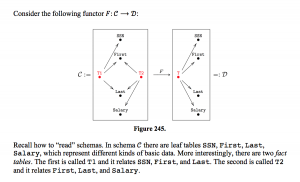
(cont.2)

51.2. Left pushforward: ∑

(cont.1)

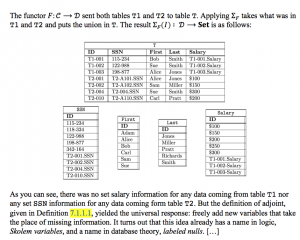
(cont.2)

51.3. Right pushforward: ∏

(cont.)

51.4. Adjoints are closed under compositions

51.5 Currying via ∆, ∑, ∏

52. CATEGORIES OF FUNCTORS

52.1 Set-valued functors

52.2. Migrating data – Application 7.2.1.2.

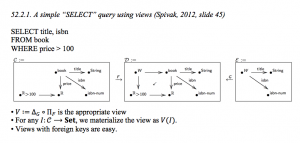
52.* A simple SELECT query using views

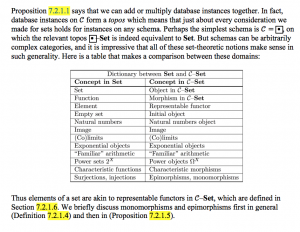
52.* Database instances on C form a topos

52.* Definition 7.2.1.4. (Monomorphism and Epimorphism)

52.3. Representable functors

(cont.1)

(cont.2)

52.4. Yoneda’s lemma

(cont.1)

(cont.2)

(cont.3)

52.5. Yoneda’s lemma, part 2