This is a sub-page of our page on Category Theory.
///////
Related KMR-pages:
• …
///////
Other relevant sources of information:
• Higher Topos Theory
• Higher Algebra
• Jacob Lurie
• Jacob Lurie’s home page
• With Category Theory, Mathematics Escapes From Equality,
by Ana Porta, Quanta Magazine
///////
From equality to equivalence – The restructuring of Mathematics:
/////// Quoting Ana Porta:
In 2006 Lurie released a draft of Higher Topos Theory on arxiv.org. In this mammoth work, he created the machinery needed to replace set theory with a new mathematical foundation, one based on infinity categories.
“He created literally thousands of pages of this foundational machinery that we’re all now using,” said Charles Rezk, a mathematician at the University of Illinois, Urbana-Champaign, who did important early work on infinity categories. “I could not imagine producing Higher Topos Theory, which he produced in two or three years, in a lifetime.”
Then in 2011, Lurie followed it up with an even longer work. In it, he reinvented algebra.
Algebra provides a beautiful set of formal rules for manipulating equations. Mathematicians use these rules all the time to prove new theorems. But algebra performs its gymnastics over the fixed bars of the equal sign. If you remove those bars and replace them with the wispier concept of equivalence, some operations become a lot harder.
Take one of the first rules of algebra kids learn in school: the associative property, which says that the sum or product of three or more numbers doesn’t depend on how the numbers are grouped: \, 2 \times (3 \times 4) \, = \, (2 \times 3) \times 4 .
Proving that the associative property holds for any list of three or more numbers is easy when you’re working with equality. It’s complicated when you’re working with even strong notions of equivalence. When you move to subtler notions of equivalence, with their infinite towers of paths between paths, even a simple rule like the associative property turns into a thicket.
A map of associations (by Jacob Lurie):
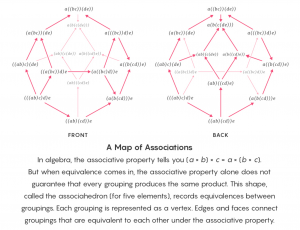
“This complicates matters enormously, in a way that makes it seem impossible to work with this new version of mathematics we’re imagining,” said David Ayala, a mathematician at Montana State University.
In Higher Algebra, the latest version of which runs to 1,553 pages, Lurie developed a version of the associative property for infinity categories — along with many other algebraic theorems that collectively established a foundation for the mathematics of equivalence.
Taken together, his two works were seismic, the types of volumes that trigger scientific revolutions. “The scale was completely massive,” Riehl said. “It was an achievement on the level of Grothendieck’s revolution of algebraic geometry.”
Yet revolutions take time, and as mathematicians found after Lurie’s books came out, the ensuing years can be chaotic.
Digesting the Cow
Mathematicians have a reputation for being clear-eyed thinkers: A proof is correct or it’s not, an idea works or it doesn’t. But mathematicians are also human beings, and they react to new ideas the way human beings do: with subjectivity, emotion, and a sense of personal stakes.
“I think a lot of writing about mathematics is done in the tone that mathematicians are searching for these glittering crystalline truths,” Campbell said. “That’s not how it goes. They’re people with their own tastes and own domains of comfort, and they’ll dismiss things they don’t like for aesthetic or personal reasons.”
In that respect, Lurie’s work represented a big challenge. At heart it was a provocation: Here is a better way to do math. The message was especially pointed for mathematicians who’d spent their careers developing methods that Lurie’s work transcended.
“There’s this tension to the process where people aren’t always happy to see the next generation rewriting their work,” Francis said. “This is one feature affecting infinity category theory, that a lot of previous work gets rewritten.”
Lurie’s work was hard to swallow in other ways. The volume of material meant that mathematicians would need to invest years reading his books. That’s an almost impossible requirement for busy mathematicians in midcareer, and it’s a highly risky one for graduate students who have only a few years to produce results that will get them a job.
Lurie’s work was also highly abstract, even in comparison with the highly abstract nature of everything else in advanced mathematics. As a matter of taste, it just wasn’t for everyone. “Many people did view Lurie’s work as abstract nonsense, and many people absolutely loved it and took to it,” Campbell said. “Then there were responses in between, including just full-on not understanding it at all.”
Scientific communities absorb new ideas all the time, but usually slowly, and with a sense of everyone moving forward together. When big new ideas arise, they present challenges for the intellectual machinery of the community. “A lot of stuff got introduced at once, so it’s kind of like a boa constrictor trying to ingest a cow,” Campbell said. “There’s this huge mass that’s flowing through the community.”
If you were a mathematician who saw Lurie’s approach as a better way to do mathematics, the way forward was lonely. Few people had read Lurie’s work, and there were no textbooks distilling it and no seminars you could take to get your bearings. “The way you had to learn about this stuff really precisely was to just sit down and do it yourself,” said Peter Haine, a graduate student at the Massachusetts Institute of Technology who spent a year reading Lurie’s work. “I think that’s the hard part. It’s not just sit down and do it yourself — it’s sit down and do it yourself by reading 800 pages of Higher Topos Theory.”
Like many new inventions, Higher Topos Theory requires mathematicians to interact a lot with the machinery that makes the theory work. It’s like making every 16-year-old hoping for a driver’s license first learn how to rebuild an engine. “If there was a more driver-friendly version, it would become instantly more accessible to a wider mathematical audience,” said Dennis Gaitsgory, a mathematician at Harvard who has collaborated with Lurie.
As people started reading Lurie’s work and using infinity categories in their own research, other problems emerged. Mathematicians would write papers using infinity categories. Reviewers at journals would receive them and say: What is this?
“You have this situation where [papers] either come back from journals with absurd referee reports that reflect deep misunderstandings, or they just take several years to publish,” Barwick said. “It can make people’s lives uncomfortable because an unpublished paper sitting on your website for years and years starts to look a little funny.”
Yet the biggest problem was not papers that went unpublished, but papers that used infinity categories and did get published — with errors.
Lurie’s books are the single, authoritative text on infinity categories. They are completely rigorous, but hard to completely grasp. They’re especially poorly suited to serving as reference manuals — it’s difficult to look up specific theorems, or to check that a specific application of infinity categories that one might encounter in someone else’s paper really works out.
“Most people working in this field have not read Lurie systematically,” said André Joyal, a mathematician at the University of Quebec in Montreal whose earlier work was a key ingredient in Lurie’s books. “It would take a lot of time and energy, so we sort of assume what’s in his book is correct because almost every time we check on something it is correct. Actually, all the time.”
The inaccessibility of Lurie’s books has led to an imprecision in some of the subsequent research based on them. Lurie’s books are hard to read, they’re hard to cite, and they’re hard to use to check other people’s work.
“There is a feeling of sloppiness around the general infinity categorical literature,” Zakharevich said.
Despite all its formalism, math is not meant to have sacred texts that only the priests can read. The field needs pamphlets as well as tomes, it needs interpretive writing in addition to original revelation. And right now, infinity category theory still exists largely as a few large books on the shelf.
“You can take the attitude that ‘Jacob tells you what to do, it’s fine,’” Rezk said. “Or you can take the attitude that ‘We don’t know how to present our subject well enough that people can pick it up and run with it.’”
Yet a few mathematicians have taken up the challenge of making infinity categories a technique that more people in their field can run with.
A User-Friendly Theory
In order to translate infinity categories into objects that could do real mathematical work, Lurie had to prove theorems about them. And to do that, he had to choose a landscape in which to create those proofs, just as someone doing geometry has to choose a coordinate system in which to work. Mathematicians refer to this as choosing a model.
Lurie developed infinity categories in the model of quasi-categories. Other mathematicians had previously developed infinity categories in different models. While those efforts were far less comprehensive than Lurie’s, they’re easier to work with in some situations. “Jacob picked a model and checked that everything worked in that model, but often that’s not the easiest model to work in,” Zakharevich said.
In geometry, mathematicians understand exactly how to move between coordinate systems. They’ve also proved that theorems proved in one setting work in the others.
With infinity categories, there are no such guarantees. Yet when mathematicians write papers using infinity categories, they often move breezily between models, assuming (but not proving) that their results carry over. “People don’t specify what they’re doing, and they switch between all these different models and say, ‘Oh, it’s all the same,’” Haine said. “But that’s not a proof.”
For the past six years, a pair of mathematicians have been trying to make those guarantees. Emily Riehl and Dominic Verity, of Macquarie University in Australia, have been developing a way of describing infinity categories that moves beyond the difficulties created in previous model-specific frameworks.
Their work, which builds on previous work by Barwick and others, has proved that many of the theorems in Higher Topos Theory hold regardless of which model you apply them in. They prove this compatibility in a fitting way: “We’re studying infinity categories whose objects are themselves these infinity categories,” Riehl said. “Category theory is kind of eating itself here.”
Riehl and Verity hope to move infinity category theory forward in another way as well. They’re specifying aspects of infinity category theory that work regardless of the model you’re in. This “model-independent” presentation has a plug-and-play quality that they hope will invite mathematicians into the field who might have been staying away while Higher Topos Theory was the only way in.
“There’s a moat you have to get across to get into this world,” Hopkins said, “and they are lowering the drawbridge.”