This page is a sub-page of our page on Geometry
///////
The interactive simulations on this page can be navigated with the Free Viewer
of the Graphing Calculator.
///////
Related KMR-pages:
• Projective Geometry
• Affine Geometry
• Metric Geometry
• Linear Transformations
• A Linear Space Probe
• Linear transformation: kernel and image (interactive)
• Dimension
• Euclidean Geometry
• Non-Euclidean Geometry
• Hyperbolic Geometry
• Elliptic Geometry
• Parabolic Geometry
• Projective Metrics
• The Euclidean Degeneration
• Geometric Shapes
• Geometric Optics
• Geometric Algebra
• David Hestenes on Geometric Algebra.
• David Hestenes on Geometric Calculus.
• David Hestenes on Conceptual Learning
• The Linear War between the planets \, V_{ectoria} \, and \, V'_{ectoria} \,
• Einstein for Flatlanders
• The Mercator Projection
• Stereographic Projection
• Conformal Mapping
• Inversion
• Möbius transformations
• Steiner Circles
• Expandable Learning Objects
• Art
• Music
• Interactive Learning Objects
• Arithmetical Crossfire
• Mathematical Cogwheels
• Numbers and their Digits in different Bases
• Having fun, with the Graphing Calculator,
Anthony Word’s internship at CID/NADA/KTH, 2 weeks in November 1999.
///////
Other related sources of information:
• Flatland – the movie 2007, based on the novel Flatland by Edwin A. Abbott from 1884.
• Flatland – the limit of our consciousness
• A Wrinkle In Time, 2018 Disney film based on the novel by Madeleine L’Engle from 1962.
• How mathematicians are storytellers and numbers are the characters
Marcus du Satoy in The Guardian, 23 January 2015.
• 3D objects for teachers in museums at the Science Museum Group.
• Kompakkt from the Department of Digital Humanities/ University of Cologne.
• Cybermath: A Shared Virtual Environment for Mathematics Exploration, by Gustav Taxén and Ambjörn Naeve, Presented at the International Conference on Distance Education, Düsseldorf, 2001.
• CyberMath: A System for Exploring Open Issues in VR-based Education, by Gustav Taxén and Ambjörn Naeve, Presented at SIGGRAPH 2001.
• 4D Toys: a box of four-dimensional toys, and how objects bounce and roll in 4D, by Miegakure on YouTube
• Wormholes Explained – Breaking Spacetime, by Kurzgesagt – in a Nutshell on YouTube.
• Dimensions – A walk through mathematics by VeganDaVinci.
• A Mathematician’s Lament by Paul Lockhart.
///////
1.1.3. MathTrek Voyager – basic concepts and ideas
The basic idea of the project is to create an adaptive and intuitive system for learning the essence of mathematics in the form of a “distributed online game”. This game – called MathTrek Voyager (MTV) – will stimulate and promote interest in mathematics by exposing the form-meaning loop that characterizes the interplay between pure and applied mathematics (see below). Hence, MTV will highlight the power of abstractions to capture many different meanings in the same form. Gaming is well suited to this task, since games have formal rules (axioms) by which they should be played, and nobody demands that such rules have any intrinsic meaning. For example, nobody says things like “I don’t understand chess because I don’t understand why the bishops move diagonally on the board.”
MathTrek Voyager exploits young people’s curiosity to explore virtual worlds with ease and fun, independent of the direct applicability of such worlds to real-world problems.
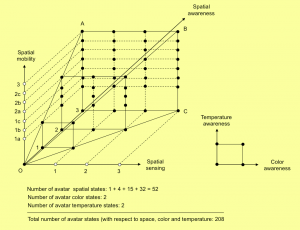
MTV will build on two classical stories: the mathematical science-fiction story of Flatland (Abbot, 1884), which was turned into a movie in 2008, and the famous TV science-fiction series Star Trek. MTV will capture the attention of the players by embedding them in a virtual hyperspace of many dimensions. Just like the spaceship Enterprise of Star Trek, the MathTrekers will be lost in (hyper)space, trying to find their way back to earth. The players (= the crew) are represented by avatars, which can change their abilities (= states) with respect to spatial awareness, spatial sensing, and spatial mobility, as well as their sensitivity to color and temperature as the game proceeds.
Succeeding in the game, players will acquire the power (i.e., the mathematical competency) to create and manipulate 1-dimensional curves, 2-dimensional surfaces, 3-dimensional solids and even 4-dimensional shapes.
These changes of competency occur at “branch points” of the game – as a result of the players’ performance in solving mathematical problems and understanding mathematical models and concepts (conceptual change, see below).
Spatial awareness and mobility:
Several players will be able to collaborate – and take responsibility for developing various parts of the mathematical skills that are needed to solve the problems that appear in the game. Building on the psychopedagogical expertise of the TU Graz team – especially CbKST (Competence-based Knowledge Space Theory) – these problems will be adapted to the skills of the players, thereby guiding them towards the goal of increasing their mathematical proficiency and understanding by mastering more and more difficult mathematical problems and concepts.
1.1.4 The form–meaning loop of mathematics and its applications
Mathematics has fought a long and hard historical battle to rid itself of meaning and transform itself into pure form. The success of this transformation is reflected in the famous statement by Bertrand Russell that “mathematics is the discipline where we do not know what we are talking about and neither whether what we are saying is true or not.” However, this development has not resulted in adequate educational changes, and today we are faced with an increasing pedagogical problem of explaining to students of mathematics the meaning of being (semantically) “meaningless” or, in other words, the power of mathematical abstraction. In the words of Hermann Weyl:
“We now come to a decisive step of mathematical abstraction: we forget about what the symbols stand for… [The mathematician] need not be idle; there are many operations which he may carry out with these symbols, without ever having to look at the things they stand for“.
Limiting mathematical concepts to their real-world instances in education makes them second-class right from the beginning – the doughnut is much more interesting than the torus which models it. It makes it difficult to understand that for some contexts (say for positioning doughnuts in a box) the torus represents the essence of the doughnut and that understanding its form is key to understanding its meaning in not just one context, may it be a doughnut box or the CERN large hadron collider.
Mathematics gives geometric objects a world to live in – and the MathTrek Voyager game puts the student right into this world’s center with the challenge of mastering it’s powers.
Put more abstractly, creating mathematics can be viewed as a de-semantization process that transforms meaning into form, while applying mathematics can be viewed as a semantization process that transforms form into meaning (by interpreting the symbols). This is the basic form-meaning loop of the interaction between mathematics and its applications, such as e.g., science and engineering. Due to this mathematics formalization process, the definition of a mathematical concept has – over many centuries – been transformed from being existential (= “What is it?” = “What does it mean?”) to becoming operational (= “How does it behave?” = “What properties does it have?”).
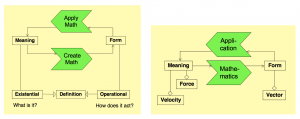
Figure 1: Creating and applying mathematics sets up a loop between meaning and form.
The right part of Figure 1 depicts how two ‘meaningful’ concepts (velocity and force) are transformed by the Mathematics abstraction process into the same ‘meaningless’ (= formal) concept of vector. The Application process transforms the formal ‘vector’ concept back to a meaningful concept by interpreting the symbols of the formal model.
The MTV project is well aware of the practical value of meaning and application. The MathTrek Voyager game foresees breakout points where the players can leave the game and apply their acquired competencies in conventional educational exercises. The key difference distinguishing MTV from conventional math courses is that it treats applications as an extra bonus of math where math education tends to present math as a necessary evil for applications.
As domain subject the project has chosen geometry for a variety of reasons. Geometry, with its origins in ancient Greece through centuries of fundamental inventions by scientists like Descartes, Bolyai, Gauss, Lobachevsky and Einstein, provides an outstanding truly European contribution to world science. Understanding and mastering geometric concepts is a basic need for many other fields – engineering, economics, physics and graphic arts to name a few. Advances in computer graphics enable new ways not only to visualize geometric objects but also interact with them. The MTV project is dedicated to explore and utilize these. Geometric objects can be efficiently described in mathematical terms – a language that is not only understood by humans all over the world but also by computers. Last but not least, geometric objects often have a natural beauty that can make interacting with them a very enjoyable aesthetic experience.
1.1.5 Reintroducing geometry in order to achieve mathematical enjoyability
MathTrek Voyager will make use of modern computer technology and psychopedagogy to introduce the material of the geometrical revolution in a comprehensible and fascinating way. It will embed the players in the story that led to such profound changes in our ideas of the space that surrounds us, and, through interactive and personalized feedback help the players to understand how we ourselves create and invent space, modifying it according to changes in our ideas of the universe.
The basic pedagogical principle that will be used to convey theses ideas is the interactive restriction of dimensions and the interchange between extrinsic and intrinsic views of 2-dimensional and 1-dimensional worlds. For example, looking at a curved surface, such as e.g. a sphere, from the outside, embedded in 3D, it is easy to understand that flat beings inhabiting its surface will be able to move straight ahead and return to the same point. However, when you are a 2D being that is living inside the spherical surface, this is not at all obvious.
By letting the players experience the change between an extrinsic and intrinsic perspective on a non-Euclidean world, we expect to be able to convey the idea that the 3D world that we inhabit can be curved in various ways, reflecting fundamental cosmological research questions.
These ideas will be further enhanced by exposing the players of MTV to 3D projections of phenomena that take place in higher dimensions, like e.g. the 3D shadows of an object that is rotating in a 4D space. The transformation of the 3D shadow will appear to be very complex, involving various changes of shape, but the 4D motion is extremely simple, being governed by a single parameter (the angle of rotation). By comparison with how 2D beings experience the projection of an object that is rotating in 3D, we expect to be able to convey the idea that when the number of spatial dimensions increase, the dynamics (transformations) in that space often becomes more simple, thereby fostering the kind of higher-dimensional viewpoint that is pursued by e.g. superstring theory, which is presently working with higher dimensional spaces to try to achieve a “Theory of Everything“.
Constructing similar (but – of course – MUCH simpler) higher dimensional views will be rewarded in the game by discovering important clues that will advance the MathTrekers towards their ultimate goal of returning to earth.
///////
Slicing a moving levelsurface ellipsoid 1
[Ambjörn Naeve on YouTube]
Slicing a moving levelsurface torus 1
[Ambjörn Naeve on YouTube]
Slicing a moving levelsurface (torus) 2:
[Ambjörn Naeve on YouTube]
///////
Intersecting the diagonal of a 3D-cube (left) and a 4D-cube (right)
with a perpendicular hyperplane (Ambjörn Naeve on YouTube)
///////
A Triact (3D-cube) is a Tesseract for Flatlanders
(Ambjörn Naeve on YouTube):
The interactive simulation that produced this movie.
Notice how the simple rotational motion of the Triact in 3D is transformed into a much more complicated transformation of its shadow in 2D. In the same way, the simple rotational motion of the Tesseract in 4D is transformed into a much more complicated transformation of its shadow in 3D.
A rotating Tesseract (4D-cube) projected into 3D-space
(throughthedoors on YouTube):
A rotating Penteract (5D-cube) projected into 3D-space
(hypercube0 on YouTube):
A rotating Hexeract (6D-cube) projected into 3D-space
(WildStar2002 on YouTube):
Unwrapping a tesseract (4d cube aka hypercube)
(Vladimir Panfilov on YouTube):
The Scan of a Tesseract in 4-dimensional space:
(Визуализации в многомерных пространствах on YouTube)
Since these ideas are naturally attractive to most human beings, we expect that our ways of exposing them to the players of MTV will have a strong impact in terms of raising the motivation and interest to study mathematics by fostering an understanding that real mathematics is “the ultimate space trip”, since mathematical research often involves the exploration of strange and wonderful spaces with surprising and exiting properties.
Moreover, MTV will emphasize the concept of symmetry, which has become so fundamental to mathematics and science, and which has such strong connections to music and art and which is accessible in its basics already at an early school age. Our approach will build on the Garden of Knowledge project (Naeve, 1997), which made innovative use of symmetry to explore and explain the connections between mathematics and music.
By adopting a didactic method that focuses on extra-curricular material, we can avoid the risk of conflicts with existing curricula. We intend no less than demonstrating that mathematical interest and competency can be achieved with greater ease by playing with abstract concepts than by avoiding them all together.
It is the overarching goal of the MTV project to change the present negative attitudes towards mathematics using modern digital media. As a consequence of this change, we expect that more motivated students will start to perform better within the mathematical curriculum, leading to better results on exams, stronger ’employability’ and increasing competitiveness for Europe in the emerging knowledge society. In fact, we strongly believe that our strategy – to aim for “employability through enjoyability” – is the most effective and efficient way to achieve this badly needed result.
1.1.6. Objectives of the MTV game
It is the overall objective of the MathTrek Voyager game to raise interest and motivation for mathematics among as many people as possible, and inspire them to learn more about the real nature of this fascinating subject. We will target players/learners between the ages of 10 and 20 with emphasis on age 16-20. Moreover, we will focus on extra-curricular content of fundamental importance to our conceptions of space and time, such as geometric transformation groups acting on sets, and geometric properties as invariants under this group action. Note that these concepts are essential ingredients of many curricular beginner math courses not only in Mathematics and Computer Science but also in Natural Sciences and Engineering.
Because we are free to focus on any type of material, we can increase our potential for awakening interest, taking advantage of existing “non-curricular connections” to physics and philosophy. We believe that achieving our overall objective of awakening mathematical interest among the players of MTV would contribute substantially towards improving their performance within the traditional mathematical curriculum, thereby drastically improving their future employability.
Our strategy for reaching this extremely ambitious objective, employability through enjoyability, is to support the players’ experience of enjoyment of mathematics. This will be achieved by involving them in an interactive, embedded, emotionally engaging, and media-rich discourse that evolves around some of the most interesting and revolutionary ideas that have ever been developed by humankind, namely the ideas of space and time that form the basis for the modern perception of our universe.
Most educational systems of today are based on a closed, layered architecture of different levels (elementary, intermediate, secondary, highschool, and university) with almost no contact between them – especially between the non-adjacent ones. An important objective of MTV is to help to overcome the thresholds between these levels that are often experienced by learners, and especially to bridge the gap between highschool and university.
Our strategy for achieving this goal is to facilitate a conceptual learning approach to the subject (Hestenes, 1995). This will be achieved by making use of different “representation schemes”, notably the Knowledge Manifold educational architecture (Naeve, 2001a; Naeve & Nilsson, 2004), which consists of a number of interlinked conceptual landscapes (context maps), where one can navigate, search for, annotate and present all kinds of electronically stored information. Such an interconnected cluster of concepts – that connects conceptual content in different contexts – we call a knowledge patch.
Representing knowledge patches in a machine-processable way and relating them to standardised competency descriptions in Competency based Knowledge Space Theory (Korossy, 1997; Albert & Lucas, 1999) opens up new ways to automate the adaptation of educational games to the needs of learners, effectively addressing both ‘forward’- and ‘backward’ competency-gaps (Naeve et al., 2008). Backward competency gaps in mathematics seem to be increasingly common among beginning university students of both pure and applied mathematics.
1.1.7. Contribution to the Objectives of the Work Programme
As described in the Work Programme, the project takes up progress in knowledge mapping and processing in the form of the Competency-based Knowledge Space Theory and utilizes it to provide advanced forms of adaptivity in a game context. This guides new forms of discovery of knowledge through new interactive geometric tools.
User-produced and game-provided content coexist in the MathTrek Voyager game universe side by side in the form of geometrically rich objects that can be individually selected and manipulated.
The development of geometry as an important part of human culture has been profoundly influenced by European science from the ancient Greeks to modern times. Thus the MTV project directly brings “new opportunities for the exploitation and sharing of Europe’s rich cultural and scientific resources. New services will engage users in new ways of experiencing and understanding cultural resources. They will enable the aggregation and annotation of objects available in digital libraries.” (Quote from work programme).
In the MTV project the MathTrek Voyager community shall take into its digital library a wealth of mathematical objects existing in various math tools and embed them into the game context as well as into the related digital documentation D1.2 “The MathTrekker’s Guide to the Universe”.
The project will not only utilize visualizations and 3D to recreate artefacts, but it will make user creation and interaction available as means of learning as well. In this way the project aims to reshape the way we learn by putting the essence of mathematics into the core of the game, strongly emphasizing exploration and inquiry-based learning. The expected learning benefits of the MTV approach are described in the following Section. Learner engagement and motivation, creativity and self-regulated exploration of the MathTrek world are key features of the project.
In its research MTV, as an interdisciplinary project, brings together current research in cognitive science and pedagogy (as described in the next section) and combines it with state of the art technology in computer graphics and serious games. A number of previous projects, on which MTV builds, are mentioned below. Moreover the MathTrek Voyager consortium is well involved in quite a number of ongoing TEL projects (see Description of the consortium).
Adaptive feedback and intuitiveness of the MathTrek Voyager game are core objectives to be realized in Work Packages 3 and 4. They are based on intimate knowledge of the subject in WP1 and pedagogic research in WP2 which will provide the basis for realizing in WP5 the affective and emotional approach of the project.
1.2 Progress beyond the state-of-the-art
The main objective of this project is the development of learning software in the form of a serious game that helps a learner to comprehend higher mathematical concepts and facilitate comprehension of abstract mathematical problems and how to approach them. Generally it can be stated, that computer games can be “rich, complex environments, that allow immersive exploration of numerous strategies for action and decision” (Facer, Ulicsak, Sandford & Futurelab, 2007, p. 46) which are able to stimulate and motivate.
The members of the consortium believe that the MTV project has a huge potential to motivate and engage learners because:
• the problems with which the learners will be confronted during their journeys through the virtual hyperspace will be challenging (e.g. McClelland, Koestner & Weinberger, 1989).
• the content will not be largely overlapping with the content of current European math curricula in schools, and it will therefore be novel for the learners.
• it will be possible to focus on the intrinsic motivation of the learners (i.e. the motivation for the content itself) and not on the extrinsic motivation, which might be central for many students in schools (e.g. the motivation to pass an exam).
• the serious game of MTV will stimulate the desire to explore and master a novel environment, which is reflected in the natural tendency of youngsters toward curiosity and exploratory play (e.g. White, 1959).
• the possibility for the learners to experience the process of passing a threshold, which may previously have prevented them from reaching a deep understanding of a concept (see section Personalized Learning Material… below on p.18).
• the possibility for a learner to learn in a collaborative way with others, especially with peers (e.g. Wentzel & Caldwell, 1997; see section Collaborative Learning Experience below p. 20).
In the following sections we will describe the state of the art of game-based learning, conceptual learning, adaptive assessment of competencies and non-cognitive aspects, current psychopedagogical trends regarding learning as well as the progress beyond the state of the art, which we will apply within this project to reach our ambitious goals to motivate and engage youngsters to explore mathematical and natural-scientific concepts.
1.2.1 Game-based Learning
It is well known that present mathematics education in Europe (and elsewhere) suffers from serious problems (ICMI, 1995). Prominent among these problems is the increasing difficulty to motivate students and maintain their interest in the subject; an interest that is almost always present at a very young age but which seems to diminish – and often to totally disappear – as the years go by. Moreover, in mathematics, the teachers at the early levels often suffer from a lack of understanding of the real nature of the subject – and e.g. often confuse mathematics with arithmetic – while the teachers at the later (university) levels often tend to consider mathematics only as a subordinate tool and don’t take the time to communicate its essence.
Serious shortcomings of traditional mathematics education include its inability to: stimulate interest, promote understanding, support personalization, facilitate transition between different levels, integrate abstractions with applications, and integrate mathematics with human culture. MathTrek Voyager will make innovative use of ICT in order to address these problems. It will build on various prior efforts – including the work of the KMR group at KTH, which has demonstrated that it is possible to increase the “cognitive contact” with mathematical concepts in many different ways. This has resulted in more than 500 interactive math programs with accompanying videos.
Moreover, MathTrek Voyager will advance the state of the art in math education by introducing the elements of:
• Mathematical Modeling (“meta-mathematics”), where mathematical structures will be presented in the form of clusters of related concepts that can be applied to problems and provide personalized hints on how to solve them and understand their underlying concepts and structure.
• Mathematical Design (i.e., constructing and testing mathematical structures), which is an activity that students rarely have an opportunity to participate in. Players will be engaged in designing mathematical structures and testing their applicability for solving the problems that they encounter in the game.
Visualization, with its vastly increased potential of modern computer graphics on low-cost hardware, provides an excellent opportunity to separate the content of mathematics from the form in which it is presented. The MTV project makes this potential accessible to education, making it possible to communicate geometry interactively in its native form at the highest extent permitted by our cognitive abilities.
1.2.2 Serious Games in Mathematics
Serious gaming promises a variety of benefits for learning. The Summit on Educational Games of the Association of American Scientists (2006) lists the following: Conceptual bridging (i.e., closing the gap between what is learned in theory and its use); High time-on-task; Motivation and goal orientation, even after failure; Providing learners with cues, hints and partial solutions to keep them progressing through learning; Personalization of learning; and Infinite patience. As revealed by a Google search for “math game“, games for learning Mathematics fall into one of two categories.
1) Isolated exercises where the learner has to provide a correct answer to a mathematical question. In these exercises the problem is described in a narrative way or the involved concepts are interpreted in an application setting (stand alone episodes).
2) Exercises as above but connected by a story. The learner moves from place to place and can proceed only if he/she solves the mathematical exercises (adventure games).
Beside these categories, there is also a large variety of tools that allow interactive experimenting with mathematical concepts. While not directly being a game, they invite the learner to play around. Producing surprising, often aesthetically appealing results, such tools also entertain and stimulate curiosity.
However, the available digital mathematical episodes as well as the mathematical adventure games lack one critical ingredient of learning and teaching: In contrast with a mathematics course, they present episodes in isolation, without reference to the inherent logical connections of the topic. Even when there is a story, the challenges are only superficially connected to it, mostly just by using in the challenges the same names of actors as in the story. Hence it is no surprise that the usual games for mathematics can be easily transferred to other topics, just by replacing the exercises. As a consequence, these games can contribute very little to stimulate interest in mathematics.
In contrast, MathTrek Voyager is a new type of game. The story will be built around the theoretical model of the topic. At the same time, this model will be represented in a machine-readable format as a Competency-based Knowledge Space. This representation will be directly used to adapt the game automatically in a way that is consistent with the natural flow of mathematical insights. In MathTrek Voyager, problems are to be solved by building new objects that continue to appear in the game and by applying precisely defined mathematical transformations to such objects.
Following the inherent logic of geometric concepts, the project will identify threshold concepts that need to be managed by the learner in order to gain particularly deep new insights. Working towards mastering those concepts can provide a direction for the game, thus avoiding the “lost in knowledge space“- phenomenon, which is only too frequent for learners.
In this way, MathTrek Voyager will realise a new kind of integration between the knowledge to be learned, the competencies to be acquired and the actual flow of the game. Moreover, without integrating them into the game, MathTrek Voyager can point learners to existing mathematical tools in order to further explore relevant objects and transformations.
Where such tools can export geometric objects in a standard way, as is the case for many computer algebra systems, possibilities will be explored to import such objects into the MathTrek Voyager game. In these ways, existing interactive math tools can augment the learning that takes place in the game.
1.2.3 Implementation within the MTV-project
Our industrial partner (Serious Games) will use the Unity3D game engine to build the game prototype. The Unity engine is among the most powerful and easy to use engines on the market, and it is the most capable engine for making browser-based games. Over the years SG has developed a number of extra features and functionalities that make it possible for us to develop games faster and better. When SG starts a project, it deploys a template with all these extra features built-in, which provides a head-start. SG has used Unity3D successfully in a number of prior learning games, including the “Global Conflicts” and the “Playing History” game series, and SG is convinced that it can use this game engine to advance the state of the art within learning games in the MTV project.
SG has a close partnership with its technology provider Unity Technologies, which enables SG to offer state-of-the-art 3D games (offline & online) by using the UNITY game engine. The game engine is cross platform, which enables SG to transfer the game prototype to a range of other platforms including PC/MAC, iPhone, Wii and Facebook if desired.
Augmenting this, the Computer Graphics Group provides particular competency in realizing real-time advanced computer graphics on low-cost hardware as well as with most immersive forms like Cave Automatic Virtual Environments using 3D glasses and data gloves. The educational potential of these technologies shall be explored from PM13 on.
1.2.4 Integrating Conceptual Learning into the Game
The MTV universe will consist of a mixture of abstract (conceptual) and concrete (image-based) structures. The players will encounter animated clusters of concepts (context-maps), which they can apply to different problem solving situations in order to figure out how to deal with them. These “live concept clusters” will provide feedback to the players and describe their interrelatedness and appropriateness for application to the specific problem that is to be solved. Innovative features of the MTV project include:
• Using a collaborative game for learning a complex subject.
• Developing a subject based on its “inner logic”, not on a curriculum. This enables a much more comprehensive understanding of the subject.
• Using cutting edge graphics technology to achieve a high degree of immersion and motivation.
• Interleaving intellectual challenge, competition, collaboration and aesthetic appeal to promote the “spirit” of the subject in an emotional way beyond mere knowledge.
• Teaching geometry, physics, space and time as the most fundamental concepts of the human understanding of the world, using a computer program not only as an illustration, but as an exploratory tool for an expedition into deep knowledge spaces, reaching beyond the limits of human imagination.
Previous projects have reacted to the desire to explore mathematics with a number of tools, which visualize certain mathematical phenomena. Some of them allow user interaction and experimentation. Many of them are known as Mathlets. The current project goes beyond this by integrating exploratory tools for a particular domain into a game environment, which continuously challenges the user.
The MTV project offers young (and elderly) people exploratory access to a world, which is not only challenging by the creatures that inhibit it, but which is challenging by the very nature of its geometry, physics, space and time. Moreover, this world is populated by bizarre forms of a beauty, which are rarely seen elsewhere. Most of these forms are described by relatively simple mathematical formulae, some – like fractals – also by simple iterative processes.
Having gained an understanding of these formulae and processes, the learner can easily modify them in an exploratory way, creating what may be seen as a piece of art, as a futuristic space ship or as a new form of planet.
Solving such challenges will require not just knowledge but real understanding of the underlying subject. Coordinates, transformations, singularities etc. are to be rapidly understood as powerful tools. Using these tools is, not by accident, required in many real world contexts too – optimization, engineering, design, robotics, and computer graphics to name a few.
The nature of geometry suggests a variety of ways to go from simple to complex challenges. One of them is to increase dimension – the dimension of objects and the dimension of the space where these objects occur in. What holds for the object holds for space as well – living in a light cone is as possible as living within a shrinking universe, with parallel universes or worm holes. Note that in this field it is often easy to pose a problem in a visually simple form where solving the problem requests understanding of abstract concepts.
A related approach, to foster understanding of fundamentals of geometry through computer graphics embedded in a story, has been undertaken recently – in 2007 – with the film Flatland – the movie. This computer-animated movie is based on the novel Flatland published in 1884(!) by E. A. Abbot. In this novel a being from 3D space visits a Victorian 2D world, which is unaware of the 3rd dimension.
Where the movie shows in a linear story how 2D beings explore a 3D world with their senses, the MTV project adds interactivity! It can provide different learners with different tools and let them collaborate.
The project exploits the potential of eLearning for personalization of knowledge acquisition as explored, for example, by the European projects ROLE, leACTIVEMATH, TRIAL-SOLUTION, PROLEARN, KALEIDOSCOPE, APOSDLE, MACE, GRAPPLE, iClass, iCamp, Revive and TenCompetence and combines it with methods used in computer games to adapt to the knowledge and preferences of learners. It complements the MKM Mathematical Knowledge Management project, which concentrates on formal Mathematics, by emphasizing sensual and immersive experience of mathematical concepts.
The project makes use of state-of-the art graphics technologies to achieve a high degree of immersion. This includes immersive 2D as well as 3D technologies. While the latter are currently mostly available in lab settings, the project paves the way for their broader educational use as it may become feasible when the 3D screens make their way into market. These technologies are currently being introduced in several European movie theaters, and they were recently presented by most major consumer electronic vendors (e.g. Panasonic, Sony, Samsung, JVC) at the IFA 2009 exhibition in Berlin.
In the MTV project technology serves learning, guided by results of current research in pedagogy, didactics and cognitive sciences as described in the next paragraphs.
1.2.5 Achieving a new quality of learning
In the MathTrek Voyager game, the learner acquires competencies by interacting with the game’s world. For such a type of learning, pedagogy provides guidance and theoretical background in the constructivist paradigm.
Constructivism in all its varieties has become the “leading […] theory or philosophy of learning in the mathematics education research community ever since […] 1987” (Ernest, 2003). The popularity of constructivism in the didactics of mathematics can be interpreted as a consequence of observances, that the learner’s conceivability is a main factor of how learning content is interpreted and received (Prediger, 2005, p. 26). Despite this popularity as a scientific paradigm, the “passive-reception view of learning is not dead among professionals or administrators in education” (Ernest, 2003), and therefore constructivism remains an ongoing challenge when planning courses, designing learning environments, preparing learning content, or performing similar activities.
Various authors (Glasersfeld, 1994, 1993; Schulmeister, 1996; Seiler, 1994) agree that Piaget laid the foundation to a constructivist oriented psychology, that suggests, that experts only have indirect influence on the knowledge mediation processes, with the introduction of the genetic epistemological psychological-theoretical framework (Hoppe-Graff & Edelstein, 1993). Piaget’s main idea is that one gains knowledge in interaction processes with the social environment.
A possible result of these processes is the adjustment of preexisting cognitive structures or the creation of new cognitive structures, which determine the behavior of a person. The subject’s cognitive structures are aspiring towards a balanced state (equilibration) between the person and its social environment. If this state is deranged, this could become a motive to gain new knowledge and new skills to recover a balanced state again. Vice versa this means that inducing conflicts can initiate cognitive processes of rearranging and reconstruction, as well as the creation of new cognitive structures and resultant behaviour.
In the early seventies of the last century, several experiments have been carried out that were using learning material based on typical Piaget problems, like dealing with constancy, set relations and inclusion problems. These problems were capable to induce cognitive conflicts, to which the learner had to respond. All in all these experiments had a positive outcome (Hoppe-Graf, 1993). Of course it would be naive to take the simple patterns of these early experiment problems and take them as a basic principle for designing learning programs and thereby expect positive results. A learning environment that aims for the goal that a learner can improve his or her understanding of abstract math problems, should rather be designed in a way that allows self-directed learning processes, and should enable learners to deal with occurring problems on their own.
The assumption underlying the concept of conflict-inducing learning settings is that successful procession of a problem and the anticipated chance of success motivates the learner intrinsically to make adequate efforts to get over his or her knowledge and skills deficits (Berlyne, 1974).
In the early eighties there were various attempts to implement the concept of inducing conflicts in class settings. Worth mentioning in the domain of mathematics are for example Bell et al (Bell, 1983, 1984, 1986; Swan, 1983; Underhill, 1991) who developed the concept of ‘Conflict teaching’ as teaching model. As an outcome it could be demonstrated that there is a correlation between conflicts in student-teacher-interaction and performance in following tests (Bell, 1984). More recently Tirosh, Stavy and Cohen (1998) engaged in research to accomplish a problem-handling, which results more from correct theoretical references made by the learner than from the application of oversimplifying error strategies. However, a change in the learner’s intuitive attitude towards a more sophisticated approach could not be demonstrated unambiguously.
As an adequate way to make use of the concept of inducing conflicts in an advanced learning setting, like the MTV game, we will follow the conceptual change approach. This approach proclaims that learners often run into issues, because “knowledge acquisition in specific domains […] sometimes requires the significant reorganization of existing knowledge structures and not just their enrichment” (Konstantinos, Vosniadou, & Vamvakoussi, 2007). In such cases there is a mismatch in the way they “use the same additive mechanisms with all forms of new knowledge making likely the formation of misconceptions” (Vosniadou & Vamvakoussi, 2005). There is no way for learners to become aware of the problems that originate from their simplified explanatory models, which they have acquired in their previous learning biography. Dealing with the aspect of misconceptions of reality and resultant conflict potentials, the conceptual change approach can provide a way of estimating potential sources of error when designing the learning game, at least as far as intentional learning processes and their possible shortcomings are concerned.
To achieve a new way of acquiring knowledge and skills, which help the learner to solve abstract mathematical problems, it should be kept in mind that “Science and mathematics […] have an objective non-situated reality, which is divorced from the processes that produced them.” (Vosniadou & Vamvakoussi, 2005). This implies that a student’s failure in resolving a mathematical problem is caused by a lack of competences, but also by a lack of specific know-how, which has to be on-hand during the examination of the challenge. The conceptual change approach suggests that didactic transformations like illustration, isolation and simplification of the learning object, can become barriers for future learning processes.
Research results related to the conceptual change approach are contradictory (Chan et al, 1997). The reason for these contradictions could possibly be that conflicts don’t necessarily lead to new insights. Beyond the cognitive aspects, there are emotional, social and motivational preconditions to be met that determine if a conflict can be successfully resolved with a gain in knowledge. (Vosniadonu, 1994; Schnotz & Carretero, 1999; Limon, 2001; Merenluoto & Lehtinen, 2003).
1.2.6. Inducing conflicts into the game design
As the previous paragraphs have shown, inducing conflict seems to be an effective and therefore worthwhile didactical principle. As a result, the concept of “conflict“ needs to be integrated into the design of the game. However, such a combination of educational goals and video games can be harder to achieve than it sounds (Wechselberger, 2009).
From a pedagogical point of view, the main benefits of computer games for educational purposes are their motivational power and the efficient learning principles they make systematic use of. However, these can only be utilized by maintaining the specific structure of video games (Fabricatore, 2000). Furthermore, Mäyra (2008) divides the structure of video games into two parts: representation and gameplay. While the representation consists of the symbols used to describe the virtual game world and allegorize the gameplay (e. g. models, textures, sound etc.), the gameplay itself might again be broken down into a hierarchy and sequence of challenges the player faces during the game (as well as the actions s/he addresses them with) (Adams & Rollings, 2007). The challenges might, among others, be logical and mathematical challenges (e. g. puzzles), factual knowledge challenges, exploration challenges (such as spatial awareness, mazes, etc.), economic challenges (e.g. achieving balance between several elements in a system), and conflict.
Not only do these challenges represent opportunities to induce conflicts into gameplay; conflict itself already is an important underlying principle of all (video) games. Indeed, the goal of most games actually consists of solving a conflict, which is often also an important part of the game’s narrative structure. For this reason, in this project it will be a major task to connect the didactical concept of conflict with the specific challenges of the gameplay.
1.2.7. Connecting the Conceptual Change Approach with Educational Games
Inducing conflicts into gameplay for didactical purposes is not the only way conflicts might enter the game. As mentioned earlier, the learners’ current knowledge might conflict with the educational content of the learning environment. Different players might have different levels of expertise, and while some of them are compatible with the game, others are not. However, this does not need to be a problem; in fact, it can actually even be utilized for the didactical concept of the game. A typical approach would be to represent these unequal and sometimes conflicting “domains of expertise” by different roles that the players can take on. For example, in the game “The Elder Scrolls IV: Oblivion” the player can be a mage, a thief, a warrior etc.; each profile provides different abilities (i.e. possible actions). Many of the game’s challenges can be addressed in different ways: While the warrior uses his enormous fighting power to get in possession of a certain artifact, the thief might just sneak up to it and steal it, making use of his distinct stealth.
Different levels of expertise on the part of the players regarding the educational content of the game may be mapped to these stereotypic character profiles/roles and therefore become a part of the game. Furthermore, different players with different profiles may join and build a team, collaboratively addressing the game’s challenges. For example, in the MathTrek Voyager game, a three-dimensional spaceman may solve a dilemma confronting a two-dimensional planeman by converting some artefacts through 3D space (as shown in Figure 2), thus illustrating the value of acquiring more complex knowledge.

Figure 2: The MathTrek Voyager.
By bringing both cooperation and conflict into the game, (a) the gameplay experience might become more interesting, (b) players might be caused to contrast their own level of expertise with the ones of their team colleagues (and thus put themselves into perspective, reflect on the boundaries of their own domains of knowledge) and (c) the game might benefit from the thereby contributed (and didactically useful) social aspects of playing and learning (cf. Meier/Seufert, 2003).
There is also a similarity between video game structure and the aforementioned threshold concepts. According to Gee (2007), during gameplay players build up a certain level of expertise, which at some point does not help them any further. At this point, they have to reorganize and expand their knowledge and abilities in order to accomplish their goal. Usually, this happens in the form of so-called “boss monsters” at the end of certain levels and parts of the game. Boss monsters are a widely established principle of game design and can naturally be associated to the didactical approach of threshold concepts.
1.2.8. Risks
There is, however, a catch when deliberately inducing conflict: Players/learners might get emotionally stressed (Sander & Heiß, 2007). In addition, Ravaja et. al. (2005) found that passive negative feedback within video games (which might be an intuitive way for a designer to create a conflict) leads to a negative emotional response. On the other hand, the same authors report that, under certain circumstances, failure might also lead to positive emotional responses. Also, Csikszentmihalyi’s concept of flow (1990), which is often applied to positive gaming experiences, states that an optimal emotional experience demands that players should neither be over- nor under challenged. As a result, conflict-induction must be handled with care, for it is a balancing act between didactical benefits and motivational risk. Exploring both this balance and methods to maintain it will be an important issue within the MathTrek Voyager project.
1.2.9. Expected Effects
Based on the above mentioned thoughts, we can formulate the following hypotheses to be verified in the MathTrek Voyager project:
• Using the structure of video games to induce conflicts will lead to higher learning effects, in particular for breaking learning barriers and acquiring higher qualities of problem solving competence.
• Conflicts can lead to emotional stress. Pedagogically guided game design, however, can reduce the risk of negative emotional responses when adaptive design takes appropriate measures.
By exploring the validity of these hypotheses in theory and practice, the MathTrek Voyager project shall advance the state of the art in pedagogic research and open up new perspectives for educational games for learning situations which are particularly critical.
1.2.10. Adaptive Assessment of Competences
A very successful approach for adaptive assessment and development of competences is the <strong>Competence-based Knowledge Space Theory (CbKST; Korossy, 1997; Albert & Lucas, 1999). The CbKST is a cognitive framework which extends the originally behaviorist Knowledge Space Theory (KST; Doignon & Falamagne, 1985, 1999). One goal of the KST is to assess the so called knowledge state of the person in an adaptive – and therefore efficient – way. It is assumed that every knowledge domain (e.g. arithmetic) can be characterized by a set of problems (i.e. test items). The knowledge state of a person is characterized by the subset of problems this person is capable to solve. It can be argued that there exists dependencies between different problems within a given domain – so called prerequisite relations. For example, because a person is able to solve problem x (e.g. multiplication), it can be assumed that this person is also able to solve problem y (e.g. addition). In this case, knowledge of addition is a prerequisite for knowledge of multiplication. </strong
The basic idea of CbKST is to assume a set of competences (skills, abilities, knowledge) underlying the problems of the given domain. Similar to the problems of a knowledge domain, prerequisite relations between competences are assumed. For example if a person is able to write a proposal for the MTV project (competence x), it can be assumed that this person is able to use a word processing software (competence y). Therefore, the ability to use word processing software is a prerequisite for the ability to write a proposal for the MTV project. The connection between the competences and problems are established by skill and problem functions.
The outlined approach of CbKST has two major advantages:
• On the one hand, given the performance, which can be observed by the subset of problems a learner can master, the latent underlying competences can be identified.
• On the other hand, effective competence development can be realized through adaptive individual learning paths based on the assumed competence space. Thus, adaptive and individualized development of competences can occur.
Recently, within the context of the ELEKTRA project (6th Framework) a new terminology was introduced: the differentiation between micro- and macro adaptive levels of competence assessment.
The so-called macroadaptivity approach is the adaptive selecting of the next problem (or “learning object”, “learning situation”) based on the competence gap of the learner which has to be closed. However, in game-based learning applications, such an explicit assessment is not appropriate, since it would disturb the gameplay and the so-called flow-experience (e.g. Csikszentmihalyi, 2008) of the playing learner. Instead there is the need for a non-invasive and continuous assessment within every single learning situation: this is the microadaptivity approach (e.g. Albert et al., 2007).
The idea behind the microadaptivity approach is to develop a system that interprets the behavior of the learner and gives appropriate interventions (e.g. hints) within a single learning situation adapted to the learner’s current knowledge and competence state. An overview of the differences between micro- and macro adaptive assessment of competences is given in Figure 3.
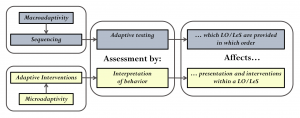
Figure 3: Overview of Macro- and Micro Adaptivity.
1.2.11. Non-invasive assessment of motivational and emotional states
A methodology for appropriate and reliable competence assessment is the starting point for the adaptive guidance through problems of a given domain with the goal of developing competences. Even if a personalized and efficient method for the adaptive guidance (i.e. development of competences) like the CbKST is available, the successful competence development of an individual is highly dependent on his/her motivational and emotional states. An overview of the dependence of the development of competences from an interaction of cognitive, motivational and emotional factors of a learner is shown in Figure 4 (adapted from Sternberg, 2007).
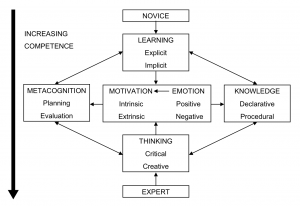
Figure 4: The transformation from a novice to an expert and the dependence of individual competence development on cognitive, motivational and emotional factors (adapted from Sternberg, 2007).
It is the goal of the MTV project to establish a methodology for the non-invasive and ongoing assessment of motivational and emotional states of the playing learner. Such an assessment of non-cognitive aspects of the learner would be a fruitful extension of the microadaptivity approach, the focus of which is currently restricted to the cognitive aspect, i.e. the non-invasive assessment of competences.
Additionally, the assessment of the motivational and emotional state of the learner would enhance the effectiveness of cognitive interventions like hints, because the reason for a possible failure of the learner to solve a problem within a single learning scenario can be identified.
For example, a hint given by an artificial mentor would be an appropriate intervention if it can be assumed that the student is not capable to solve a problem within a learning scenario because of cognitive reasons. In this case it would be assumed that at least one necessary competence is missing. But the appropriateness of such a hint would be low if we would know that the learner would be able to solve the problem but that (s)he is not motivated to do so – maybe because the problem is too easy. In this case, a hint which was given only on the base of the assessment of the cognitive state would degrade the learner’s current motivational state and would be counter-productive for the possibility of flow experiences, because such experiences typically only occur if the task is challenging enough (Csikszentmihalyi, 2008).
The possibility to enhance the motivation in a non-invasive way by motivational interventions – and therefore the non-invasive assessment of the current motivational state – is important, if not necessary to achieve the goals of the MTV project. It is necessary, because we are not focusing on a target group which is already highly interested in mathematical issues and which is already motivated to solve mathematical problems. We want to awaken the interest in mathematical issues in those who are not already interested, and we want to enhance the motivation for solving mathematical problems in those who are not motivated yet.
1.2.12. Personalized Competence Development
Using CbKST it is possible to provide the learner with personalized and efficient learning paths through the competence space. Such learning paths can be traversed by guiding the learner successively through different and increasingly extensive competence states. By passing through such a learning path, the learner can be provided with the possibility to change from a novice to an expert (see Figure 4).
The development of competences will be secured by providing the learners with explanatory material. This explanatory material will be collected within WP1 (Vision and Content) and will be selected and (if necessary) improved within WP2 (Pedagogy). Due to the dependencies between learning material (such as written documents, videos, simulations etc.) analogous to the prerequisite relations between competences (described in section 1.2.10), the learner can be provided with learning material which is appropriate for his / her current competence state. Such personalized presentation of learning material was successfully implemented within the EC-funded project iClass (6th FP).
1.2.13. Personalized learning material through involvement of learning strategies and preferences
Concepts which could be learned by playing the MTV game, such as dimensions, symmetry or multidimensional transformations to name a few, seem to be similar to so-called threshold concepts, which have been recently introduced by Meyer and Land (2003, 2005).
Meyer and Land (2003) suggest that threshold concepts have five characteristics. They are:
• transformative (they shift the perception of the learner within the knowledge domain),
• irreversible (once it has been understood, the learner is unlikely to forget a threshold concept)
• integrative (they expose a previously hidden interrelatedness of different aspects of the knowledge domain)
• bounded (a threshold concept helps to define the boundaries of a subject area).
• troublesome (a threshold concept may be counter-intuitive).
It can be assumed that there exist a large number of potential threshold concepts within the domain of mathematics (e.g. Worsley, Bulmer & O`Brien, 2008; Easdown, 2008). Deep and sophisticated knowledge of mathematical issues is meaningless until the student has acquired a profound understanding of the involved concepts.
In order to make new ways of competence devolvement feasible, the MTV project will take such potential threshold concepts (TCs) into account and will define possible approaches to integrate TCs or similarly defined anchor concepts (see Mead et al., 2006) with the CbKST. One possible approach to integrate TCs with the CbKST might be to differentiate two competence spaces: a competence space for knowledge and a competence space for understanding of threshold concepts (see Figure 5).
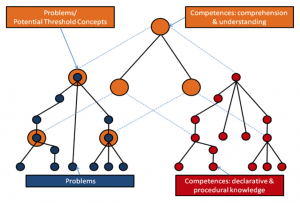
Figure 5: Differentiation between two kinds of competences: comprehension and knowledge.
We propose two different strategies when someone tries to get a deep and sophisticated understanding of a troublesome and counter-intuitive concept:
• the inductive strategy: the learner tries to understand different, concrete and relatively small knowledge units in the first step (red circles) to get successively “a view of the whole picture” (orange circles, i.e. to understand the more abstract and broader concepts).
• the deductive strategy: the learner tries to understand the concept in the first step (orange circles), so that it is in consequence much easier – or maybe not necessary any more – to learn the single knowledge-units consecutively (red circles).
Taking into account individual preferences related to the strategies for understanding troublesome concepts will enhance the possibility of providing the learner with personalized or “customized” learning material. Additionally, it would constitute another fruitful extension of the CbKST, because new and even more efficient learning paths (e.g. from one TC to the next) would be possible if the learner prefers to use such a learning strategy.
1.2.14. Changing attitudes towards mathematics
The MTV project aims at positively changing the players’ attitudes towards mathematics, since it is a central educational goal of the project to foster the mathematical interest of the playing learners. To this end, the Person-Object theory of Interest (POI) provides an integrative framework. From the perspective of POI, an interest-driven action results from the individual, as a potential source of action, as well as from an aspect of the environment (situation), as the object of action. Together they form a dynamic unit.
Thus interest is considered as a relational construct, referring to a “person-object-relation”. This relation is characterized by several specific features including cognitive aspects, feeling- and value-related aspects and the intrinsic quality of interest-based actions (Krapp, 2002). Thus POI enriches the MTV approach by a powerful conceptual framework to explain the dynamics of interest development due to both personal and environmental influences. It includes important affective aspects of learning, which have relevance especially for serious games. Moreover, POI informs the MTV project on how to design interesting learning environments with the perspective to foster the development of long-lasting individual subject interest in mathematics.
From a cognitive perspective, two aspects of interest are especially important (Krapp, 2002). Firstly, interest develops over time, and structural components of the personality change with respect to both cognitive and emotional representations. Secondly, interest tends to grow, which means that the person wants to test and acquire new information and to enlarge his/her competences with respect to the object of interest. In addition, interests possess emotional and value-related characteristics. The value-related characteristics can be seen as value-related valences (Schiefele, 1999), which the individual assigns to the goals, contents and activities related to the domain of interest, and which express the personal significance of the interest.
The emotional characteristics of interest can be described as positive feeling-related valences (Schiefele, 1996), which consist of states and experiences preceding, accompanying or following an interest-driven activity (e.g. joy, feelings of competence, autonomy and social relatedness), and which are stored in a person’s cognitive-emotional representation system (Krapp, 2002). Overall, most aspects of an interest-triggered action are connected with positive emotional experiences. Under extremely congenial conditions, flow may be experienced (Csikszentmihalyi, 1988).
Therefore, interest-based actions can be characterized by optimal experiential modes that combine positive cognitive qualities (e.g. personal significance) and positive affective qualities (e.g. good mood). Thus interest is strongly associated with the concept of “undivided interest” or “serious play” which is used by Rathunde, 1998, to describe an optimal mode of task engagement. From the perspective of POI, an interest-based action also possesses an intrinsic quality, which is characterized by an optimal combination of emotional and value-oriented components of interest (Krapp, 2002). There is no difference between what one has to do in a specific situation and what one likes to do.
1.2.15. Collaborative Learning Experience
The serious game that will result from the MTV project will be playable in two different modes: as a single player or as a multiplayer game. The opportunity of collaborative learning through a multiplayer game is the starting point of a scientific challenge for the consortium as a whole, and in particular for the TUG-KMI team with its expertise of the CbKST approach. The CbKST has until now not been implemented in projects and applications which focus on competence assessment and development of groups.
In a multiplayer game it is necessary to assess a “collective” competence state of the learning group’s members, in order to examine which problems are challenging enough for the group as a whole. We propose that such a collective competence state can be computed through set inclusion of the individual competence states of the group members.
As described in section 1.1 (Concept and Objectives), the avatars of the learners can have different abilities with respect to spatial awareness, spatial sensing, spatial mobility (all of these abilities have 4 values: 0, 1, 2, and 3 dimensions) as well as their sensitivity to color and temperature. All possible combinations of the different values of abilities can be termed (avatar) ability states. Groups whose members control avatars with different ability states have to work together, i.e. in a collaborative way, to solve problems in the virtual space. The experience that every member (respectively their avatar) has different abilities, and that every member is equally needed for the group as a whole, can be a fruitful starting point for collaborative learning and the exchange of knowledge.
1.3 S/T methodology and associated work plan
Overall strategy of the work plan
MathTrek Voyager is based on the inner structure of the subject (WP1) and on pedagogic principles for individual and collaborative learning (WP2). These Work Packages contribute to the development of domain models (WP1) and models of learners and individual as well as collaborative learning processes (WP2). These models then form the basis for the design and implementation of the adaptation and guidance mechanisms in WP3. A game utilizing these adaptation mechanisms is designed in WP4. WP5 implements this design and creates the game ready for playing. WP6 has the learners in focus. It connects them beyond collaboration in the game through a common platform and disseminates the project results. The experience from WP6 is analysed and evaluated in WP7, which in turn advances pedagogic theory in WP2, the appropriate selection of problems in WP1to improve guidance in WP3 and game design in WP4 as well as the implementation in WP5. WP8 (Management) ensures smooth collaboration of all Work Packages.
With respect to the key objectives mentioned above, WP1 not only provides the content to be learned, it also provides the abstract challenges needed to ensure entertainment, packaged in WP4 and WP5. WP2 strengthens individual and collaborative learning. WP3 keeps the learning manageable for the learner. WP4 (Game Design) and WP5 (Implementation) have major responsibility for the affirmative, immersive character of the learning experience. Collaboration on a larger scale is supported by WP6 and the learning outcomes and learning experience are evaluated by WP7.
The project will proceed in four overlapping phases.
• Preparation Phase (Month 1-12). In this phase the state of the art in the various fields will be explored in detail and summarized in respective Deliverables. This includes summarizing requirements to educational games in mathematics from the points of view of pedagogy, technology and usability. Given the truly interdisciplinary character, this phase serves two purposes
• Explain relevant findings from the different fields (Mathematics, Educational Games, Adaptivity, Computer Graphics,…) to the partners as a basis for communication in the Consortium.
• Establishing a baseline for further work.
• Planning Phase (Month 7-24). In the planning phase, detailed learning objectives, concept maps, user models, game control rules, graphics and interactivity design, evaluation criteria etc. will be defined.
• Implementation Phase (Months 13 – 30). This phase will implement the MathTrek Voyager game. It is subdivided into two sub phases.
• Experimental phase (Months 13-18). In this phase isolated episodes of the game will be developed, often in several variants – for example 2D vs. 3D variant, single player vs. collaborative, self-regulated vs. guided learning – to explore their suitability in various learning contexts.
• Production phase (Months 19 – 30) This phase will gradually implement the final version of the game.
• Evaluation Phase (Months 13 – 36) This phase starts with developing the evaluation concept w.r.t. learning outcomes, competency development, user satisfaction, usability and technical quality. Actual evaluation shall start with pre-tests and proceed to usage evaluation as components of the game become available.
The realization of these phases through the individual work packages and their dependencies are depicted in the following charts.
///////
REFERENCES
• Abbott, E. A. & Stewart, I. (2002),
The annotated Flatland – a romance of many dimensions. New York: Basic Books.
• Abbott, E. A. (1884),
Flatland: A Romance of Many Dimensions. With an introduction by A.K. Dewdney. New York
• Adams, E. & Rollings, A. (2007),
Fundamentals of Game Design. New Jersey: Prentice Hall
• Albert, D. Lukas, J. (Eds.) (1999),
Knowledge Spaces: Theories, Empirical Research, and Applications. Mahwah, NJ: Lawrence Erlbaum Associates
• Albert, D., Hockemeyer, C., Kickmeier-Rust, M. D., Peirce, N., Conlan, O. (2007),
Microadaptivity within complex learning situations –- a personalized approach based on competence structures and problem spaces. Poster presented at International Conference on Computers in Education (ICCE 2007)
• Bell, A. (1983),
Diagnostic teaching of additive and multiplicative problems. In R. Hershkowitz (Ed.), Proceedings of the Seventh International Conference for the Psychology of Mathematics Education (pp. 205-210). Rehovot, Israel: Weizmann Institute of Science
• Bell, A. (1984),
Short and long term learning – experiments in diagnostic teaching design. In B. Southwell, R. Eyland, M. Cooper, J. Conroy & K. Collis (Eds.), Proceedings of the Eighth International Conference for the Psychology of Mathematics Education (pp. 55-62). Darlinghurst: Mathematical Association of South Wales, Australia
• Bell, A. (1986),
Outcomes of the diagnostic teaching project. In L. Burton & C. Hoyies (Eds.), Proceedings of the Tenth International Conference for the Psychology of Mathematics Education (pp. 331-335). London: University of London
• Berlyne, D. E. (1974),
Konflikt, Erregung, Neugier. Zur Psychologie der kognitiven Motivation. Stuttgart: Klett
• Chan, C.K.K, Burtis, P.J., Bereiter, C. (1997),
Knowledge-building approach as a mediator of conflict in conceptual change. Cognition and Instruction. 1997, 15(1), 1-40
• Conway, J. H., Burgiel, H., Goodman-Strauss, C. (2008),
The Symmetries of Things, A. K. Peters Ltd., Wellesley, Massachusetts, 2008, ISBN 978-1-56881-220-5
• Csikszentmihalyi, M. (1988),
The flow experience and its significance for human psychology. In M. Csikszentmihalyi & I.S. Csikszentmihalyi (Eds.). Optimal experience: Psychological studies of flow in consciousness. New York: University Press
• Csikszentmihalyi, M. (1990),
Flow: The Psychology of Optimal Experience. New York: Harper and Row
• Csikszentmihalyi, M. (2008),
Flow: The Psychology of Optimal Experience. New York: Harper Collins Publishers.
• Doignon, J., Falmagne, J. (1985),
Spaces for the assessment of knowledge. International Journal of Man-Machine Studies, 23, 175–196
• Doignon, J.P., Falmagne, J.C. (1999),
Knowledge spaces. Berlin: Springer
• Easdown, D. (2007),
The role of proof in mathematics teaching and The Plateau Principle. Proceedings of the Assessment in Science Teaching and Learning Symposium, Sydney, 28−33
• Ernest, P. (2003),
Reflections on Theories of Learning. In Zentralblatt für Didaktik der Mathematik (Bd. 38, p. 3-7). Eggenstein-Leopoldshafen
• Fabricatore, C. (2000),
Learning and videogames: An unexploited synergy. AECT National Convention, Long Beach
• Facer, K., Ulicsak, M., Sandford, R. & Futurelab (2007)
Can computer games go to school? In British Educational Communications and Technology Agency (Eds). Emerging Technologies for Learning. Computer games in education. (Available at: http://www.becta.org.uk/research)
• Federation of American Scientists (2006),
Summit on educational games. (Available at: http://www.fas.org/gamesummit/Resources/Summit%20on%20Educational%20Games.pdf)
• Gee, J. P. (2007),
Good Video Games and Good Learning: Collected Essays on Video Games, Learning and Literacy. New York: Peter Lang
• Glasersfeld, E. V. (1993),
Introduction. In E. V. Glasersfeld (Ed.). Radical Constructivism in mathematics education. Dordrecht: Kluwer Academic Publishers
• Glasersfeld, E. V. (1994),
Piagets konstruktivistisches Modell: Wissen und Lernen. In G. Rusch & J. Schmidt (Ed.). Piaget und der Radikale Konstruktivismus. Frankfurt a. M.: Suhrkamp
• Henrichwark, C. and Gräsel, C. (2009),
Claudia Henrichwark and Cornelia Gräsel, Motivation im Mathematikunterricht – Zum Einsatz einer integrierten Lernumgebung im 2. Schuljahr, in: C. Röhner, C. Henrichwark, and M. Hopf (Eds.), Europäisierung der Bildung, VS Verlag für Sozialwissenschaften (2009), pp. 291-285
• Hestenes, D., Rockwood., A., Naeve, A., Doran C., Lasenby J., Dorst, L., Mann, S. (2001),
Geometric Algebra: New Foundations, New Insights,
Advanced 1-day course organized by Alyn Rockwood and Ambjörn Naeve and delivered at SIGGRAPH 2000 and 2001
• Hoppe-Graff, S., (1993),
Sind Konstruktionsprozesse beobachtbar? In W. Edelstein & S. Hoppe-Graff (Ed.). Die Konstruktion kognitiver Strukturen: Perspektiven einer konstruktivistischen Entwicklungspsychologie Bern: Hans Huber
• Hoppe-Graff, S., Edelstein, W., (1993),
Einleitung: Kognitive Entwicklung als Konstruktion. In W. Edelstein & S. Hoppe-Graff (Ed.). Die Konstruktion kognitiver Strukturen: Perspektiven einer konstruktivistischen Entwicklungspsychologie. Bern: Hans Huber
• International Commission on Mathematics Instruction (ICMI) (1995),
Perspectives on the Teaching of Geometry for the 21st Century, Educational Studies in Mathematics, Volume 28, Number 1, January, 1995, ISSN 0013-1954
• Knudsen, C., Naeve, A., (2002),
Presence Production in a Distributed Shared Virtual Environment for Exploring Mathematics, in Soldek, J., Pejas, J., (eds), Advanced Computer Systems, pp. 149-159, Kluwer Academic Publishers, 2002, ISBN 0-7923-7651-X
• Konstantinos, P. C., Vosniadou, S., Vamvakoussi, X., (2007),
Students’ Interpretations of Literal Symbols in Algebra. In S. Vosniadou, A. Baltas, & X. Vamvakoussi (Ed.). Re-Framing the Conceptual Change Approach in Learning and Instruction, Advances in Learning and Instruction Series. Oxford: Elsevier Press
• Korossy, K., (1997),
Extending the theory of knowledge spaces: A competence-performance approach. Zeitschrift für Psychologie, 205, 53-82
• Krapp, A., (2002),
An educational-psychological theory of interest and its relation to self-determination theory. In Deci, E.L. & Ryan, R.M. (Eds.). The handbook of self-determination research. Rochester: University of Rochester Press. P. 405-427
• Lepper, M. R., and Malone, T. W., (1987),
Intrinsic motivation and instructional effectiveness in computer-based education, in: R. E. Snow, and M. J. Farr (Eds.), Aptitude, Learning, and Instruction, III: Conative and Affective Process Analysis, Hillsdale, NJ: Lawrence Erlbaum Associates (1987), pp. 255-286.
• Limon, C., (2001),
On the cognitive conflict as an instructional strategy for concep-tual change: a critical appraisal. In Learning and instruction, 2001, Vol. 11, Nr. 4-5, 357-380
• Livio, M., (2005),
The Equation That Couldn’t Be Solved – How Mathematical Genius Discovered the Language of Symmetry, Simon & Schuster, New York, 2005, ISBN 0-285-63743-6.
• Massey, L., (2007),
Contrast Learning for Conceptual Proximity Matching, in: 2007 International Conference on Machine Learning and Cybernetics, Volume 7 (2007), pp. 4044-4049
• Mäyra , F., (2008),
An Introduction to Game Studies: Games in Culture. Los Angeles: SAGE Publications
• McClelland, D.C., Koestner, R., Weinberger, J., (1989),
How does self-attributed and impicit motives differ? Psychological Review, 96, 690-702
• Mead, J., Gray, S., Hamer, J., James, R., Sorva, J., St. Clair, C., Thomas, L., (2006),
A cognitive approach to identifying measurable milestones for programming skill acquisition, Annual Joint Conference Integrating Technology into Computer Science Education, Bologna, 26-28
• Meier, C., Seufert, S., (2003),
Game–based learning: Erfahrungen mit und Perspektiven für digitale Lernspiele in der betrieblichen Bildung.; In A. Hohenstein Wilbers (Eds.) Handbuch E–Learning für Wissenschaft und Praxis. Köln: Deutscher Wirtschaftsdienst
• Merenluoto, K., Lehtinen, E., (2003),
Number concept and conceptual change: Outlines for new teaching strategies. Unpublished paper of a lecture on the 10th Biennial Conference on Learning and Instruction (EARLI) in August 2003 in Padova, Italy
• Meyer, J., Land, R., (2003),
Threshold concepts and troublesome knowledge: Linkages to ways of thinking and practicing within the disciplines. ETL Project: Occasional Report
• Meyer, J., Land, R., (2005),
Threshold concepts and troublesome knowledge (2): Epistemological considerations and a conceptual framework for teaching and learning. Higher Education, 49, 373-388
• Naeve, A., (1997),
The Garden of Knowledge as a Knowledge Manifold – a Conceptual Framework for Computer Supported Subjective Education, CID-17, TRITA-NA-D9708, Department of Numerical Analysis and Computer Science, KTH, Stockholm.
• Naeve, A., (2000),
The Garden of Knowledge – an interactive system for exploring mathematics, presented at Siggraph2000, New Orleans, July 25, 2000
• Naeve, A., (2001a),
The Knowledge Manifold – an educational architecture that supports inquiry-based customizable forms of E-learning, Proceedings of the 2nd European Web-Based Learning Environments Conference, October 24–26, Lund, Sweden
• Naeve, A., (2001b),
The Work of Ambjörn Naeve within the Field of Mathematics Educational Reform, CID-110, TRITA-NA-D0104, KTH, Stockholm, 2001.
• Naeve, A., Karlgren, K. Nilsson, M., Jansson, K., (2002),
MathViz: Shared Mathematical Courselets and Interactive Visualizations, Progress report from the PADLR project within the Wallenberg Global Learning Network
• Naeve, A., Nilsson, M., (2003),
ICT-enhanced Mathematics Education within the Framework of a Knowledge Manifold, Presented at PICME 10, the Swedish Preconference to ICME 2004, Växjö, May 9-11, 2003
• Naeve, A., Sicilia, M-A., Lytras, M., (2008),
Learning processes and processing learning: From Organizational Needs to Learning Designs, Journal of Knowledge Management, Special Issue on Competencies Management, Vol 12, No. 6, December 2008
• Naeve, A., Svensson, L., (2001),
Geo-Metric-Affine-Projective unification, in Sommer, G. (ed), Geometric Computing using Clifford Algebra, Ch. 5 (pp. 105-126), Springer, 2001, ISBN 3-540-41198-4
• Neward. T., (2008),
Rethinking Enterprise, Video recording from his speech at a software developers conference in San Francisco, 2008.
• Nilsson, M., Naeve, A., (2003),
On designing a global infrastructure for content sharing in mathematics education, Presented at PICME 10, the Swedish Preconference to ICME 2004, Växjö, May 9-11, 2003
• Polya, G., (2004).
How to Solve It: A New Aspect of Mathematical Method (with a foreword by John, H., Conway), Princeton University Press, 2004 (1945), ISBN13: 978-0-691-11966-3
• Prediger, S., (2005),
“Auch will ich Lernprozesse beobachten, um besser Mathematik zu verstehen.” Didaktische Rekonstruktion als mathematikdidaktischer Forschungsansatz zur Restrukturierung von Mathematik. In Pädagogische Hochschule Schwäbisch Gmünd, Institut für Mathematik und Informatik (Ed.). mathematica didactica. Zeitschrift für die Didaktik der Mathematik, 28. Schwäbisch Gmünd
• Rathunde, K., (1998),
Undivided and abiding interest. Comparisons across studies of talented adolescents and creative adults. In L. Hofmann, A. Krapp, A. Renninger & J. Baumert (Eds.). Interest and Learning. Proceedings of the Seeon-Conference on Interest and Gender (pp. 367-376). Kiel: IPN
• Ravaja, N., Saari, T. Laarni, J., Kallinen, K., Salminen, M., (2005),
The Psychophysiology of Video Gaming: Phasic Emotional Responses to Game Events. In Proceedings of DiGRA 2005 Conference: Changing Views – Worlds in Play
• Rocard, M., Csermely, P., Jorde, D., Lenzen, D., Wahlberg-Henriksson, H., Hemmo, V., (2007),
Science Education Now: A Renewed Pedagogy for the Future of Europe, European commission, Community Research, 2007
• Sander, E., Heiß, A., (2007),
Konfliktinduzierung beim Lernen mit Neuen Medien. In D. Lemmermöhle, M. Rothgangel, S. Bögeholz, M. Hasselhorn & R. Watermann (Eds.) Professionell lehren – erfolgreich lernen. Berlin: Waxmann
• Schiefele, U., (1996),
Motivation und Lernen mit Texten. Gottingen, Germany: Hogrefe
• Schiefele, U., (1999),
Interest and learning from text. Scientific Studies of Reading, 3, p. 257-279
• Schnotz, W., Vosniadou, S., Carretero, M., (1999),
Preface. In W. Schnotz, S. Vosniadou & M. Carretero (Eds.). New perspectives on conceptual change. Oxford: Elsevier Science
• Schöllhorn, W., (1987),
Wolfgang Schöllhorn, Differenzielles Lehren und Lernen von Bewegung. Durch veränderte Annahmen zu neuen Konsequenzen, in: Hartmut Gabler/Ulrich Göhner/Frank Schiebl (Hg.), Zur Vernetzung von Forschung und Lehre in Biomechanik, Sportmotorik und Trainingswissenschaft, Hamburg (2005), pp. 125-135.
• Schulmeister, R., (1996),
Grundlagen hypermedialer Lernsysteme: Theorie – Didaktik – Design. Bonn: Addison-Wesley
• Seiler, T., (1994),
Ist Jean Piagets strukturgenetische Erklärung des Denkens eine konstruktivistische Theorie? In G. Rusch & S. J. Schmidt (Ed.). Piaget und der Radikale Konstruktivismus. Frankfurt a. M.: Suhrkamp
• Sternberg, R., (2007),
Intelligence, Competence, and Expertise. In A. J. Elliot & C. D. Dweck (Eds.). Handbook of competence and motivation. New York: Guilford Press
• Swan, M., (1983),
Teaching decimal place value: A comparative study of “conflict” and “positive only” approaches. In R. Hershkowitz (Ed.), Proceedings of the Seventh International Conference for the Psychology of Mathematics Education (pp. 211-216). Rehovot, Israel: Weizmann Institute of Science
• Taxén, G., Naeve, A., (2001), CyberMath: A Shared Virtual Environment for Mathematics Exploration, Proceedings of the 20:th World Conference on Open Learning and Distance Education (ICDE-2001), Düsseldorf, Germany, April 1-5, 2001
• Taxén G., Naeve, A., (2001b),
CyberMath – Exploring Open Issues in VR-based Learning, SIGGRAPH 2001, Educators Program, SIGGRAPH 2001 Conf. Abstracts and Applications, pp. 49-51.
• Tirosh, D., Stavy, R., Cohen, S., (1998),
Cognitive Conflict and intuitive rules. In International Journal of Science Education 20, 1257-1269
• Underhill, R. G., (1991),
Two layers of constructivist curricular interaction. In E. von Glasersfeld (Ed.), Radical constructivism in mathematics education (229-248). Dordrecht: Kluwer Academic Publishers
• Vosniadou, S., (1994),
Capturing and modeling the process of conceptual change. In Special Issue on Conceptual Change, Learning and Instruction, 4 (S. 45-69)
• Vosniadou, S., Vamvakoussi, X., (2005),
Examining mathematics learning from a conceptual change point of view: Implications for the design of learning environments. In F. Verschaffel, F. Dochy, M. Boekaerts, & S. Vosniadou (Eds.). Instructional psychology: Past, present and future trends -Fifteen essays in honour of Erik De Corte. Advances in Learning and Instruction Series. Elsevier
• Wechselberger, U., (2009),
Teaching Me Softly: Experiences and Reflections on Informal Educational Game Design. In Pan, Zhigeng; Cheok, Adrian David; Müller, Wolfgang, El Rhabili, Abdennour (Eds.): Transactions on Edutainment II. LNCS Vol. 5660. Berlin: Springer, p90–104
• Wentzel, K. R., Caldwell, K., (1997),
Friendships, peer acceptance, and group membership: Relations to academic achievement in middle school. Child Development, 68, 1198-1209
• White, R. W., (1959),
Motivation reconsidered: The concept of competence. Psychological Review, 66, 297-333
• Widmaier, M., (2007),
Differenzielles Lernen. Sachgemäßes Üben im Randbereich des Lösungsraums, in: Üben & Musizieren 3 (2007), pp. 48-51.
• Winroth, H., (1999),
Dynamic Projective Geometry, Ph. D. dissertation, KTH/NA/R–99/01–SE, Department of Numerical Analysis and Computer Science, KTH, Stockholm, March 1999.
• Worsely, S., Bulmer, M., O’Brien, M., (2007),
Threshold concepts and troublesome knowledge in a second level mathematics course. Proceedings of the Assessment in Science Teaching and Learning Symposium, Sydney, 139−144
///////
///////
Flatland – the movie
(Dano Johnson on YouTube):
///////
Flatland – the limit of our consciousness
(delphys75 on YouTube):
///////
Flatland The Movie – Tony Hale as King of Pointland
(JeffreyTravis on YouTube):
///////
Flatland: Reflections
(FlatlandTheFilm on YouTube):
///////
HyperSpace
Sphereland – Teaser Trailer
(Dano Johnson on YouTube):
///////
Hypersphere 2
(WildStar2002 on YouTube):
///////
Hypersphere 4
(WildStar2002 on YouTube):
///////
A Breakthrough in Higher Dimensional Spheres
(PBS Infinite Series on YouTube):
///////
Thinking outside of the 10-dimensional box
(Steven Strogatz on YouTube):
///////
A torus meets an equation
(Hotel Infinity on YouTube):
///////
Hypertorus
(WildStar2002 on YouTube):
///////
Exploring a 6D hypertorus
(tarkuk on YouTube):
///////
Moebius Story: Wind and Mr. Ug
(Vihart on YouTube):
///////
Moebius highway
(daveszcz on YouTube):
///////
The Klein bottle
(bothmer on YouTube):
///////
Cyclist on a Klein bottle
(rambetter on YouTube):
///////
The adventures of the Klein bottle
(mathemamovies on YouTube):
///////
///////
Perfect shapes (= Platonic bodies) in higher dimensions
(Numberphile on YouTube):
///////
The sixth Platonic solid is called the 120-cell.
It consists of 120 regular dodecahedrons interconnected in 4D-space:
120-cell rotating in 4D
(Rob Scharein on YouTube):
///////
• List of regular polytopes and compounds
///////