The Universal Knowledge Evolution Process | Knowledge Management Research Group

This page is a sub-page of our page on Knowledge Algebra.

///////

Related KMR pages:

• Stories
• Traps
• The Universal Discourse
• Laurent Expansion of Time into a Series of Moments
• The Chain Rule
• ForeSight and HindSight Process Manager in Knowledge Algebra

///////

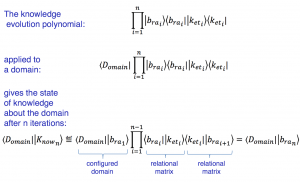
The Universal Knowledge Evolution Formula
(using postfix operational notation):

///////

Below we will be using prefix operational notation, for the reason that it is compatible with matrix algebra.

\, {M_{ilestone}}_{\, 0} \, = \, S_{tart} \, = C_{onfig} \,

///////

\, \langle \, {M_{ilestone}}_{\, n} \, \vert \, \vert \, D_{omain} \, \rangle \, = \, \langle \, {M_{ilestone}}_{\, n} \, \vert \, \vert \, {M_{ilestone}}_{ \, n - 1} \, \rangle \, \langle \, {M_{ilestone}}_{\, n - 1} \, \vert \, \vert \, D_{omain} \, \rangle \,

\, \langle \, {M_{ilestone}}_{\, n} \, \vert \, \vert \, D_{omain} \, \rangle \, = \, \lgroup \, \displaystyle\prod_{i = 0}^{n - 1} \, \langle \, {M_{ilestone}}_{\, i + 1} \, \vert \, \vert \, {M_{ilestone}}_{ \, i} \, \rangle \, \rgroup \, \langle \, S_{tart} \, \vert \, \vert \, D_{omain} \, \rangle \,

///////

\, \langle \, {A_{nnotations}}_{\, n} \, \vert \, \vert \, D_{omain} \, \rangle \, = \, \langle \, {A_{nnotations}}_{\, n} \, \vert \, \vert \, {A_{nnotations}}_{ \, n - 1} \, \rangle \, \langle \, {A_{nnotations}}_{\, n - 1} \, \vert \, \vert \, D_{omain} \, \rangle \,

\, \langle \, {A_{nnotations}}_{\, n} \, \vert \, \vert \, D_{omain} \, \rangle \, = \, \lgroup \, \displaystyle\prod_{i = 0}^{n - 1} \, \langle \, {A_{nnotations}}_{\, i + 1} \, \vert \, \vert \, {A_{nnotations}}_{ \, i} \, \rangle \, \rgroup \, \langle \, S_{tart} \, \vert \, \vert \, D_{omain} \, \rangle \,

///////

\, \langle \, {S_{tories}}_{\, n} \, \vert \, \vert \, D_{omain} \, \rangle \, = \, \langle \, {S_{tories}}_{\, n} \, \vert \, \vert \, {S_{tories}}_{ \, n - 1} \, \rangle \, \langle \, {S_{tories}}_{\, n - 1} \, \vert \, \vert \, D_{omain} \, \rangle \,

///////

\, {S_{tories}}_{\, 0} \, = \, S_{tart} \, = C_{onfig}

\, \langle \, {S_{tories}}_{\, n} \, \vert \, \vert \, D_{omain} \, \rangle \, = \, \lgroup \, \displaystyle\prod_{i = 0}^{n - 1} \, \langle \, {S_{tories}}_{\, i + 1} \, \vert \, \vert \, {S_{tories}}_{ \, i} \, \rangle \, \rgroup \, \langle \, S_{tart} \, \vert \, \vert \, D_{omain} \, \rangle \,

///////

\, \cdots \, \langle \, {N_{ext}}^3 \, \vert \, \vert \, {N_{ext}}^2 \rangle \, \langle \, {N_{ext}}^2 \, \vert \, \vert \, {N_{ext}}^1 \, \rangle \, \langle \, {N_{ext}}^1 \, \vert \, \vert \, N_{ow} \, \rangle \, \langle \, N_{ow} \, \vert \, \vert \, {L_{ast}}^1 \, \rangle \, \langle \, {L_{ast}}^1 \, \vert \, \vert \, {L_{ast}}^2 \, \rangle \, \langle \, {L_{ast}}^2 \, \vert \, \vert \, {L_{ast}}^3 \, \rangle \, \cdots \,

$\, {L_{ast}}^1 = {N_{ext}}^{-1} \,$ .

///////
Connect with the Laurent expansion of Time into a series of Moments.
///////

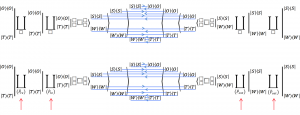
< Evaluation(next) > < Construction(now) > < Evaluation(last) > … knowlecular chain:

\, \langle \, {R_{esources}}_{\, n + 1} \, \vert \, \vert \, {G_{oals}}_{\, n + 1} \, \rangle \, \langle \, {G_{oals}}_{\, n + 1} \, \vert \, \vert \, {R_{esources}}_{\, n} \, \rangle \, \langle \, {R_{esources}}_{\, n} \, \vert \, \vert \, {G_{oals}}_{\, n} \, \rangle \,

\, \overset{\underrightarrow{\;\;\; \text{How well next?} \;\;\;}} { \langle \, {R_{esources}}_{\, n + 1} \, \vert \, \vert \, {G_{oals}}_{\, n + 1} \, \rangle } \, \overset{\underleftarrow{\;\;\; \text{How act now?} \;\;\;}} { \langle \, {G_{oals}}_{\, n + 1} \, \vert \, \vert \, {R_{esources}}_{\, n} \, \rangle } \, \overset{\underrightarrow{\;\;\; \text{How well last?}\;\;\;}} { \langle \, {R_{esources}}_{\, n} \, \vert \, \vert \, {G_{oals}}_{\, n} \, \rangle } \,

///////

\, \cdots \, \langle R_2 \vert \vert G_2 \rangle \, \langle G_2 \vert \vert R_1 \rangle \, \langle R_1 \vert \vert G_1 \rangle \, \langle G_1 \vert \vert R_0 \rangle \,

///////

\, \langle \, a \, \vert \, \vert \, c \, \rangle \, = \, \langle \, a \, \vert \, \vert \, b \, \rangle \, \langle \, b \, \vert \, \vert \, c \, \rangle \, = \, \begin{pmatrix} a_1 b_1 & a_1 b_2 \\ a_2 b_1 & a_2 b_2 \end{pmatrix} \, \begin{pmatrix} b_1 c_1 & b_1 c_2 \\ b_2 c_1 & b_2 c_2 \end{pmatrix} \, = \, \begin{pmatrix} a_1 (b_1 b_1 + b_2 b_2) c_1 & a_1 (b_1 b_1 + b_2 b_2) c_2 \\ a_2 (b_1 b_1 + b_2 b_2) c_1 & a_2 (b_1 b_1 + b_2 b_2) c_2 \end{pmatrix} \,

///////

\, \langle \, a \, \vert \, \vert \, b \, \rangle \, {\langle \, a \, \vert \, \vert \, b \, \rangle}^{\text{T}} = \langle \, a \, \vert \, \vert \, b \, \rangle \, \langle \, b \, \vert \, \vert \, a \, \rangle \, = \, \begin{pmatrix} a_1 b_1 & a_1 b_2 \\ a_2 b_1 & a_2 b_2 \end{pmatrix} \, \begin{pmatrix} b_1 a_1 & b_1 a_2 \\ b_2 a_1 & b_2 a_2 \end{pmatrix} \, = \, \begin{pmatrix} a_1 (b_1 b_1 + b_2 b_2) a_1 & a_1 (b_1 b_1 + b_2 b_2) a_2 \\ a_2 (b_1 b_1 + b_2 b_2) a_1 & a_2 (b_1 b_1 + b_2 b_2) a_2 \end{pmatrix} \,

///////

\, \langle \, a \, \vert \, \vert \, b \, \rangle \, \langle \, b \, \vert \, \vert \, c \, \rangle \, \langle \, c \, \vert \, \vert \, d \, \rangle \, = \, \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} \, \begin{pmatrix} b_1 & b_2 \end{pmatrix} \begin{pmatrix} b_1 \\ b_2 \end{pmatrix} \, \begin{pmatrix} c_1 & c_2 \end{pmatrix} \, \begin{pmatrix} c_1 \\ c_2 \end{pmatrix} \, \begin{pmatrix} d_1 & d_2 \end{pmatrix} \, =

\, = \, \begin{pmatrix} a_1 b_1 & a_1 b_2 \\ a_2 b_1 & a_2 b_2 \end{pmatrix} \, \begin{pmatrix} b_1 c_1 & b_1 c_2 \\ b_2 c_1 & b_2 c_2 \end{pmatrix} \, \begin{pmatrix} c_1 d_1 & c_1 d_2 \\ c_2 d_1 & c_2 d_2 \end{pmatrix} \, = \, \begin{pmatrix} a_1 (b_1 b_1 + b_2 b_2) (c_1 c_1 + c_2 c_2) d_1 & a_1 (b_1 b_1 + b_2 b_2) (c_1 c_1 + c_2 c_2) d_2 \\ a_2 (b_1 b_1 + b_2 b_2) (c_1 c_1 + c_2 c_2) d_1 & a_2 (b_1 b_1 + b_2 b_2) (c_1 c_1 + c_2 c_2) d_2 \end{pmatrix} \,

///////

\, \begin{pmatrix} a_1 \\ \vdots \\ a_{n_a} \end{pmatrix} \, \overbrace{(b_1 \, \ldots \, b_{n_b}) \begin{pmatrix} b_1 \\ \vdots \\ b_{n_b} \end{pmatrix}}^{({b_1}^2 + \, \ldots \, + {b_{n_b}}^2)} \, \overbrace{(c_1 \, \ldots \, c_{n_c}) \begin{pmatrix} c_1 \\ \vdots \\ c_{n_c} \end{pmatrix}}^{({c_1}^2 + \, \ldots \, + {c_{n_c}}^2)} \, (d_1 \, \ldots \, d_{n_d}) \, =

\, = \, \begin{pmatrix} a_1 \\ \vdots \\ a_{n_a} \end{pmatrix} \, ({b_1}^2 + \, \ldots \, + \, {b_{n_b}}^2) \, ({c_1}^2 + \, \ldots \, + \, {c_{n_c}}^2) \, (d_1 \, \ldots \, d_{n_d}) \, =

$\, = \, \begin{pmatrix} a_1 ({b_1}^2 + \, \ldots \, + {b_{n_b}}^2) \, ({c_1}^2 + \, \ldots \, + {c_{n_c}}^2) d_1 & \ldots & a_1 ({b_1}^2 + \, \ldots \, + {b_{n_b}}^2) \, ({c_1}^2 + \, \ldots \, + {c_{n_c}}^2) d_{n_d} \\ \vdots & \ldots & \vdots \\ a_{n_a} ({b_1}^2 + \, \ldots \, + {b_{n_b}}^2) \, ({c_1}^2 + \, \ldots \, + {c_{n_c}}^2) d_1 & \ldots & a_{n_a} ({b_1}^2 + \, \ldots \, + {b_{n_b}}^2) \, ({c_1}^2 + \, \ldots \, + {c_{n_c}}^2) d_{n_d} \end{pmatrix}$ .

///////

Definition: $\, n_{abcd} \stackrel{\text{def}}{=} n_a \, n_b \, n_c \, n_d \,$

///////

The semantic path equivalence graph:

Consider a $\, n_{abcd}$ -by- $n_{abcd} \,$ matrix $\, G \,$ with elements $\, G_{ik} = 1 \,$ if the graph $\, G_i \,$ is path equivalent to the graph $\, G_k \,$ , and $\, G_{ik} = 0 \,$ if it is not. The indices $\, i \,$ and $\, k \,$ each range from $\, 1 \,$ to $\, n_{abcd}$ .

Serial connection of knowlecules:

$\, (p_{re}) \, \vert \, a \, \rangle \, \langle \, a \, \vert \, (p_{ost}) \, (p_{re}) \, \vert \, b \, \rangle \, \langle \, b \, \vert \, (p_{ost})$ .

Parallel connection of knowlecules:

$\, (p_{re}) \, \bigg \vert \, \begin{matrix} (p_{re}) \, \vert \, a \, \rangle \\ (p_{re}) \, \vert \, b \, \rangle \end{matrix} \, \bigg \rangle \, \bigg \langle \, \begin{matrix} \langle a \, \vert \, (p_{ost}) \\ \langle b \, \vert \, (p_{ost}) \end{matrix} \, \bigg \vert \, (p_{ost})$ .

Combination of parallel and serial connections:

///////

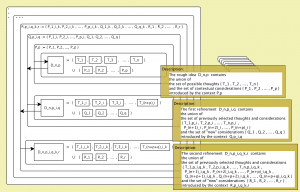
Recursive Business Logic:

///////

Thoughts and ideas in different contexts – meta 1, 2, 3:

///////

Evolving interactions between Old(m-1) and New(m):

\langle O_0 || O_0 \rangle \,

\begin{pmatrix} \langle O_0 || O_0 \rangle & \langle O_0 || N_1 \rangle \\ \langle N_1 || O_0 \rangle & \langle N_1 || N_1 \rangle \end{pmatrix} \, \longrightarrow \, \langle O_1 || O_1 \rangle \,

\begin{pmatrix} {\begin{pmatrix} \langle O_0 || O_0 \rangle & \langle O_0 || N_1 \rangle \\ \langle N_1 || O_0 \rangle & \langle N_1 || N_1 \rangle \end{pmatrix}} & \langle O_1 || N_2 \rangle \\ \langle N_2 || O_1 \rangle & \langle N_2 || N_2 \rangle \end{pmatrix} \, \longrightarrow \, \langle O_2 || O_2 \rangle \,

\begin{pmatrix} {\begin{pmatrix} {\begin{pmatrix} \langle O_0 || O_0 \rangle & \langle O_0 || N_1 \rangle \\ \langle N_1 || O_0 \rangle & \langle N_1 || N_1 \rangle \end{pmatrix}} & \langle O_1 || N_2 \rangle \\ \langle N_2 || O_1 \rangle & \langle N_2 || N_2 \rangle \end{pmatrix}} & \langle O_2 || N_3 \rangle \\ \langle N_3 || O_2 \rangle & \langle N_3 || N_3 \rangle \end{pmatrix} \, \longrightarrow \, \langle O_3 || O_3 \rangle \,

\begin{pmatrix} \begin{pmatrix} {\begin{pmatrix} {\begin{pmatrix} \langle O_0 || O_0 \rangle & \langle O_0 || N_1 \rangle \\ \langle N_1 || O_0 \rangle & \langle N_1 || N_1 \rangle \end{pmatrix}} & \langle O_1 || N_2 \rangle \\ \langle N_2 || O_1 \rangle & \langle N_2 || N_2 \rangle \end{pmatrix}} & \langle O_2 || N_3 \rangle \\ \langle N_3 || O_2 \rangle & \langle N_3 || N_3 \rangle \end{pmatrix} & \langle O_3 || N_4 \rangle \\ \langle N_4 || O_3 \rangle & \langle N_4 || N_4 \rangle \end{pmatrix} \, \longrightarrow \, \langle O_4 || O_4 \rangle \,

\begin{pmatrix} \begin{pmatrix} \begin{pmatrix} {\begin{pmatrix} {\begin{pmatrix} \langle O_0 || O_0 \rangle & \langle O_0 || N_1 \rangle \\ \langle N_1 || O_0 \rangle & \langle N_1 || N_1 \rangle \end{pmatrix}} & \langle O_1 || N_2 \rangle \\ \langle N_2 || O_1 \rangle & \langle N_2 || N_2 \rangle \end{pmatrix}} & \langle O_2 || N_3 \rangle \\ \langle N_3 || O_2 \rangle & \langle N_3 || N_3 \rangle \end{pmatrix} & \langle O_3 || N_4 \rangle \\ \langle N_4 || O_3 \rangle & \langle N_4 || N_4 \rangle \end{pmatrix} & \langle O_4 || N_5 \rangle \\ \langle N_5 || O_4 \rangle & \langle N_5 || N_5 \rangle \end{pmatrix} \, \longrightarrow \, \langle O_5 || O_5 \rangle \,

///////

Recursive formulation:

For positive integers $\, m \,$ we have:

\, \langle \, O_m \, || \, O_m \, \rangle \, \longleftarrow \, \begin{pmatrix} \langle \, O_{m-1} \, || \, O_{m-1} \, \rangle & \langle \, O_{m-1} \, || \, N_m \, \rangle \\ \;\;\; \langle \, N_m \, || \, O_{m-1} \, \rangle & \;\;\; \langle \, N_m \, || \, N_m \, \rangle \end{pmatrix} \,

///////

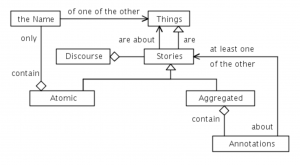
Atomic and Aggregated Stories:

///////

{
“@context”:
“id”:
“type”: “Story”
“body”: {
“type”: “Story”
“sources”: List of Stories and other Things that this Story is referring to
“purpose”: “describing”
“selector”: {
“type”: FragmentSelector”,
“conformsTo”:
“value”:
}
}
“target”: {
“type”: “List of Stories”
}
}

///////

{
“@context”:
“id”:
“type”: “Atomic Story”
“body:” {
“type”: “Name”
}
“target”: {
“type”: “Thing\Story”
}
}

///////

{
“@context”:
“id”:
“type”: “Aggregated Story”
“body:” {
“type”: “Story”
}
“target”: {
“type”: “List of Stories”
}
}

///////

Leave a Reply Cancel reply