This page is a sub-page of our page on The Human Category.
///////
Related KMR pages:
• Algebra
• Social Algebra
• Socially Responsible Algebra
• Entropy
• The Entropy Law and the Economic Process
• Category Theory
• Asynchronous Public Service
• CHARGE (Cultural Heritage Asynchronous Research Grid Environment)
• MATCH (MAthematical Transformations for Cultural Heritage)
• Mediating Human Interaction
///////
Books:
• Algebraic Theories, by Ernest G. Manes, Springer, 1976.
///////
Other related sources of information:
• Functorial Semantics of Algebraic Theories, by F. William Lawvere, 1968 (1963).
• Semiotic Engineering
• Algebraic Semiotics, by Joseph Goguen
///////
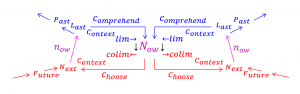
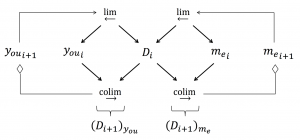
The now pulls back the Now (via the Last) and transforms it into the Next:
Pulling back a pattern through a pre-pattern creates a post-pattern:
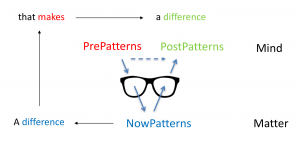
A difference that makes a difference:
///////
How a difference makes a difference:
///////
\, {\mathbb 2}^{P_{rePatterns}} \, \stackrel {N_{owPatterns}} {\longrightarrow} \, {\mathbb 2}^{P_{ostPatterns}} \, \, {\mathbb 2}^{P_{rePats}} \, \stackrel {N_{owPats}} {\longrightarrow} \, {\mathbb 2}^{P_{ostPats}} \,• Expansion of Time into a Laurent series of moments
///////
///////
/////// Quoting Manes (1976, p.1):
“Groups,” “rings,” and “lattices” are definable in the language of finitary operations and equations. “Compact Hausdorff spaces” are also equationally definable except that the requisite operations (of ultrafilter convergence) are quite infinitary. On the other hand, systems of structured sets such as “topological spaces” cannot be presented using only operations and equations.
While “topological groups” is not equational when viewed as a system of sets with structure, when viewed as a system of “topological spaces with structure” the additional structure is equational; here we must say equational “over topological spaces.”
The program of this book is to define for a “base category” \, \mathscr{K} \, – a system of mathematical discourse consisting of objects whose structure we “take for granted” – categories of \, \mathscr{K} -objects with “additional structure,” to classify where the additional structure is “algebraic over \, \mathscr{K} ,” to prove general theorems about such algebraic situations, and to present examples and applications of the resulting theory in diverse areas of mathematics.
/////// End of Quote from Manes (1976)
/////// Quoting Manes (1976, p.161):
Chapter 3: Algebraic Theories in a Category
This chapter serves as an introduction to categorical universal algebra. Necessary and sufficient conditions for a functor \, U : \mathscr{A} \longrightarrow \mathscr{K} \, to be a category of algebras are provided. Theories in \, \mathscr{K} \, are interpreted as monoids in the category of endofunctors of \, \mathscr{K} .
Epimorphic quotient theories characterize the abstract Birkhoff subcategories; when the base category is regular, the Birkhoff subcategory generated by a class \, \mathscr{A} \, of algebras is the class of all quotients of subalgebras of products of elements of \, \mathscr{A} .
As a generalization of topological algebra, for each fibre-complete category \, \mathscr{C} \, over \, \mathbf{Set} the category of all \, (X, s, \xi) \, with a \, \mathscr{C} -structure and \, (X, \xi) \, a T-algebra in such a way that the T-operations are admissible in \, \mathscr{C} \, is seen to be algebraic over \, \mathscr{C} .
Given two algebraic theories in \, \mathbf{Set} , the category of bialgebras – the two sorts of operations commute with each other – is studied; it is often itself algebraic. A general colimit theorem is applied to prove that many categories of algebras have small colimits.
/////// End of Quote from Manes (1976)