This page is a sub-page of our page on Mathematical Concepts
///////
The sub-pages of this page are:
• Equivalence
• Preorder
• Partial order
• Total order
///////
Related KMR-pages:
• Representation and Reconstruction of Numbers.
• Numbers and their Digits in different Bases.
• Shift of Basis (in general).
• Mathematics is Representation
• Homology and Cohomology
• Quotients
• Topology
• Duality
• Dimension
• Entropy
• Uncertainty
///////
Other relevant sources of information:
///////
The interactive simulations on this page can be navigated with the Free Viewer
of the Graphing Calculator.
///////
A list of anchors into the text below:
• Three different types of order relations
• Equivalence relations
• Least Common Multiple and Greatest Common Divisor of two integers
• An important fact
• Hasse diagrams
• Interactive exercises
• Prime numbers
• Representing rational numbers
• Extension and reduction of fractions
• Adding rational numbers in fractional representation
• Visualization of the addition formula
• Rational numbers as periodic decimal expansions
• Representing rational polynomials
• Polynomial fractions
• Adding rational polynomials in fractional representation
• Addition formula for two polynomial fractions
• Extension and reduction of polynomial fractions
///////
Definition: A binary relation on a set \mathcal X is a subset R \subseteq \mathcal X \times \mathcal X .
If (x, y) \in R we say that x is related to y and we write xRy .
A binary relation R on \mathcal X is called:
• reflexive if xRx \, \forall x \in \mathcal X .
• transitive if xRy \, \text{and} \, yRz \Rightarrow xRz \, , \forall x, y,z \in \mathcal X .
• symmetric if xRy \Rightarrow yRx \, , \forall x, y \in \mathcal X .
• antisymmetric if xRy \, \text{and} \, yRx \Rightarrow x=y \, , \forall x, y \in \mathcal X .
///////
Three different types of order relations
A preorder relation is a binary relation which is reflexive and transitive.
A partial order relation is a binary relation which is reflexive, transitive, and antisymmetric.
A total order relation is a partial order relation such that xRy or yRx holds \forall x, y \in \mathcal X .
Hence a partial order relation is an antisymmetric preorder relation, and a total order relation is a partial order relation such that every pair of elements in the underlying set are included in the relation.
Equivalence relations
An Equivalence relation is a binary relation which is reflexive, transitive, and symmetric.
Important fact: An equivalence relation partitions the underlying set into disjoint subsets.
///////
Least Common Multiple (lcm) and Greatest Common Factor (gcf) of two integers
Let \, \mathrm{P} = \{p_1, p_2, p_3, \dots\} = \{2, 3, 5, \dots\} \, denote the set of all prime numbers.
As proved by Euclid a long time ago, \, \mathrm{P} \, is an infinite set.
The unique prime factorizations of the integers \, m \, and \, n \, can be expressed as
\, m = \prod\limits_{ i \, \in \, \{ i \, : \, m_i \neq 0 \} }^{} {p_i}^{m_i} \; respectively \, n = \prod\limits_{ i \, \in \, \{ i \, : \, n_i \neq 0 \} }^{} {p_i}^{n_i} .
The integers m_i \, and \, n_i \, represent the number of times the prime factor \, p_i \, appears
in the prime factorizations of \, m \, respectively \, n .
Moreover, the least common multiple of \, m \, and \, n \, is
\, \mathrm{lcm} (m, n) = \prod\limits_{i \, \in \, \{ i \, : \, \max (m_i,n_i) \neq 0 \}}^{} {p_i}^{\max (m_i,n_i)} \;
and and the greatest common factor of \, m \, and \, n \, is
\, \mathrm{gcf} (m, n) = \prod\limits_{i \, \in \, \{ i \, : \, \min (m_i,n_i) \neq 0 \}}^{} {p_i}^{\min (m_i,n_i)} \, .
Since every integer [is finite, its prime factorization only contains a finite number of primes and therefore each of the four products above only contains a finite number of factors.
Hence we have
\, m \, \times \, n \, = \,
\, = \, \prod\limits_{ i \, \in \, \{ i \, : \, m_i \neq 0 \} }^{} {p_i}^{m_i} \, \times \, \prod\limits_{ i \, \in \, \{ i \, : \, n_i \neq 0 \} }^{} {p_i}^{n_i} \, = \, \prod\limits_{ i \, \in \, \{ i \, : \, \max (m_i,n_i) \neq 0 \} }^{} {p_i}^{m_i \, + \, n_i} \, =
\, = \prod\limits_{i \, \in \, \{ i \, : \, \max (m_i,n_i) \neq 0 \}}^{} {p_i}^{\max (m_i,n_i) \, + \, \min (m_i,n_i)} \, =
\, = \prod\limits_{i \, \in \, \{ i \, : \, \max (m_i,n_i) \neq 0 \}}^{} {p_i}^{\max (m_i,n_i)} \, \times \, \prod\limits_{i \, \in \, \{ i \, : \, \min (m_i,n_i) \neq 0 \}}^{} {p_i}^{\min (m_i,n_i)} \, =
\, = \mathrm{lcm} (m, n) \, \times \, \mathrm{gcf} (m, n) .
Thus we have proved the following important fact:
\, m \, \times \, n \, = \, \mathrm{lcm} (m, n) \, \times \, \mathrm{gcf} (m, n) \, .
A visual proof of this fact (based on the unique prime factorization theorem for integers)
can be outlined like this:
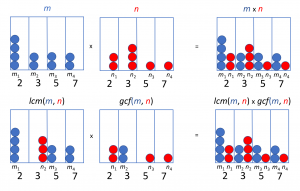
///////
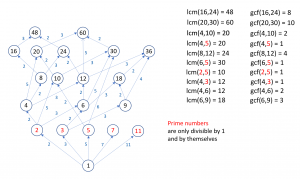
Hasse diagrams
Part of a Hasse diagram for the positive integers:
This kind of Hasse diagram can be seen as a multiplication table that higlights the role of prime numbers as well as the role of the least common multiple and the greatest common factor of two integers. Moreover, Hasse diagrams are useful to visualize any partially ordered set, such as for example the power set (= the set of all subsets) of a given set. In this case, the union and intersection of two subsets play a role that is analogous to the lcm and gcf of two integers.
A Hasse diagram of the set of all subsets (= the power set) of \, \{1, 2, 3, 4 \} :
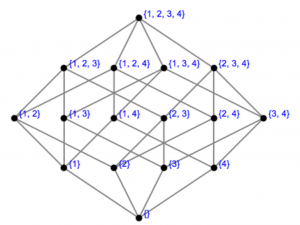
Both the integers (under division) and the power set of a given set (under union and intersection) are examples of a more general partially ordered structure called a lattice.
• Hasse diagrams at Math24.net
• Hasse Diagrams of integer Divisors
(at http://demonstrations.wolfram.com/HasseDiagramsOfIntegerDivisors/)
• Upward and downward closures (of an element of a partially ordered set)
Interactive exercises:
Mathematical Cogwheels
Primes Factory
Prime numbers
• Why do prime numbers make these spirals?
• The Riemann Hypothesis, Explained The Riemann hypothesis is the most notorious unsolved problem in all of mathematics. Ever since it was first proposed by Bernhard Riemann in 1859, the conjecture has maintained the status of the “Holy Grail” of mathematics. In fact, the person who solves it will win a $1 million prize from the Clay Institute of Mathematics. So, what is the Riemann hypothesis? Why is it so important? What can it tell us about the chaotic universe of prime numbers? And why is its proof so elusive? Alex Kontorovich, professor of mathematics at Rutgers University, breaks it all down in this comprehensive explainer.
///////
Representing rational numbers
Fractions
Rational numbers can be formally defined as equivalence classes of pairs of integers \, (p, q) \, with \, q ≠ 0 , using the equivalence relation defined as follows:
\, (p_1 , q_1) \sim (p_2 , q_2) \iff p_1 q_2 = p_2 q_1 .
This relation \, \sim \, is:
• reflexive, because \, (a_1 , b_1) \sim (a_1 , b_1) \, since \, a_1 b_1 = a_1 b_1 .
• symmetric, because if \, (a_1 , b_1) \sim (a_2 , b_2) \, then \, a_1 b_2 =a_2 b_1 \, and therefore we have \, (a_2 , b_2) \sim (a_1 , b_1) .
• transitive, because if \, (a_1 , b_1) \sim (a_2 , b_2) \, and \, (a_2 , b_2) \sim (a_3 , b_3) ,
then \, a_1 b_2 = a_2 b_1 and \, a_2 b_3 = a_3 b_2 , and therefore \, (a_1 b_2)(a_2 b_3) = (a_2 b_1)(a_3 b_2) .
Hence we have \, a_1 b_3 = a_3 b_1 and therefore \, (a_1 , b_1) \sim (a_3 , b_3) .
Hence the relation \, \sim \, is an equivalence relation.
Definition: The fraction \, \dfrac{p}{q} \, denotes the equivalence class of \, (p, q) .
Extension and reduction of fractions
Since \, (np)q = (nq)p \, we see that if \, n \neq 0 we have \, (np , nq) \sim (p , q) and therefore \, \frac{np}{nq} \, = \, \frac{p}{q} . Multiplying or dividing the nominator and the denominator of a fraction by the same non-zero integer \, n \, is called extending respectively reducing the fraction by \, n . This means choosing a different representative for the equivalence class of the rational number behind the fraction.
Let \, m \, be a non-zero integer. Extending a fraction \, \frac{p}{q} by \, m \, is always possible, but reducing it by \, m \, is only possible if \, m \, is a common factor of its nominator and its denominator. If \, m \, is the greatest common factor of \, p \, and \, q , that is if \, m = \mathrm{gcf}(p,q) , then the fraction \, \frac{\frac{p}{m}}{\frac{q}{m}} \, is called maximally reduced or irreducible.
No further reduction is possible since the nominator and the denominator of this fraction have no common factor greater than one, that is we have \, \mathrm{gcf}(\frac{p}{m},\frac{q}{m}) = 1 . Two such integers are called coprime, relatively prime or mutually prime.
Adding rational numbers in fractional representation
Let \, a, b, c, d \in \mathbb{Z} \, and let \, b, d \neq 0 . Then we have
\, \dfrac{a}{b} + \dfrac{c}{d} = \dfrac{ad}{bd} + \dfrac{bc}{bd} = \dfrac{ad + bc}{bd} = \dfrac{\dfrac{ad + bc}{\mathrm{gcf}(b,d)}} {\dfrac{bd}{\mathrm{gcf}(b,d)}} = \dfrac{\dfrac{ad + bc}{\mathrm{gcf}(b,d)}} {\mathrm{lcm}(b,d)} \in \mathbb{Q} .
Hence we have shown the following addition formula for two fractions :
\, \dfrac{a}{b} + \dfrac{c}{d} = \dfrac{\dfrac{ad + bc}{\mathrm{gcf}(b,d)}} {\mathrm{lcm}(b,d)} .
Note that both the nominator and the denominator of \, \frac{ad + bc}{bd} \, are divisible by \, \mathrm{gcf}(b,d) \, since either \, b \, or \, d \, appears in each of the terms of the nominator. There may, however, be common factors remaining in the nominator and the denominator of the fraction that represents the sum of the two rational numbers. For example, the addition formula above will result in the computation \, \frac{1}{2} + \frac{1}{2} = \frac{2 + 2}{2 \cdot 2} = \frac{4}{4} = \frac{2}{2} .
Visualization of the addition formula:
\, \frac{1}{2} + \frac{1}{3} = \frac{6}{12} + \frac{4}{12} = \frac{10}{12} = \frac{5}{6} .
///////
Rational numbers as periodic decimal expansions
//// TEXT HERE
Representing rational polynomials:
Rational polynomials can be formally defined as equivalence classes of pairs of polynomials \, (p, q) \, with \, q ≠ 0 , using the equivalence relation defined as follows:
\, (p_1 , q_1) \sim (p_2 , q_2) \iff p_1 q_2 = p_2 q_1 .
This relation \, \sim \, is:
• reflexive, because \, (a_1 , b_1) \sim (a_1 , b_1) \, since \, a_1 b_1 = a_1 b_1 .
• symmetric, because if \, (a_1 , b_1) \sim (a_2 , b_2) \, then \, a_1 b_2 =a_2 b_1 \, and therefore we have \, (a_2 , b_2) \sim (a_1 , b_1) .
• transitive, because if \, (a_1 , b_1) \sim (a_2 , b_2) \, and \, (a_2 , b_2) \sim (a_3 , b_3) ,
then \, a_1 b_2 = a_2 b_1 and \, a_2 b_3 = a_3 b_2 , and therefore \, (a_1 b_2)(a_2 b_3) = (a_2 b_1)(a_3 b_2) .
Hence we have \, a_1 b_3 = a_3 b_1 and therefore \, (a_1 , b_1) \sim (a_3 , b_3) .
Hence the relation \, \sim \, is an equivalence relation.
///////
Polynomial fractions
Definition: The polynomial fraction \, \dfrac{p}{q} \, denotes the equivalence class of \, (p, q) .
///////
Adding rational polynomials in fractional representation
Let \, a, b, c, d \, be polynomials and let \, b, d \neq 0 . Then we have
\, \dfrac{a}{b} + \dfrac{c}{d} = \dfrac{ad}{bd} + \dfrac{bc}{bd} = \dfrac{ad + bc}{bd} = \dfrac{\dfrac{ad + bc}{\mathrm{gcf}(b,d)}} {\dfrac{bd}{\mathrm{gcf}(b,d)}} = \dfrac{\dfrac{ad + bc}{\mathrm{gcf}(b,d)}} {\mathrm{lcm}(b,d)} \in \mathbb{Q} .
Hence we have shown the following Addition formula for two polynomial fractions :
\, \dfrac{a}{b} + \dfrac{c}{d} = \dfrac{\dfrac{ad + bc}{\mathrm{gcf}(b,d)}} {\mathrm{lcm}(b,d)} .
Note that both the nominator and the denominator polynomial of \, \frac{ad + bc}{bd} \, are divisible by \, \mathrm{gcf}(b,d) \, since either \, b \, or \, d \, appears in each of the terms of the nominator polynomial. There may, however, be common factors remaining in the nominator and the denominator of the polynomial fraction that represents the sum of the two rational polynomials. For example, the addition formula above will result in the computation
\, \dfrac{x^2}{x^2 + y^2} + \dfrac{y^2}{x^2 + y^2} = \dfrac{x^2 (x^2 + y^2) + y^2 (x^2 + y^2)}{(x^2 + y^2)(x^2 + y^2) } = \dfrac{(x^2 + y^2)^2}{(x^2 + y^2)^2} = \dfrac{x^2 + y^2}{x^2 + y^2}
///////
Extension and reduction of polynomial fractions
Let \, p, q, n \, be polynomials. Since \, (np)q = (nq)p \, we see that if \, n \neq 0 we have \, (np , nq) \sim (p , q) and therefore \, \frac{np}{nq} \, = \, \frac{p}{q} . Multiplying or dividing the nominator and the denominator of a polynomial fraction by the same non-zero polynomial \, n \, is called extending respectively reducing the polynomial fraction by \, n . This means choosing a different representative for the equivalence class of rational polynomials behind the polynomial fraction.
Let \, m \, be a non-zero polynomial. Extending a polynomial fraction \, \frac{p}{q} by \, m \, is always possible, but reducing it by \, m \, is only possible if \, m \, is a common factor of its nominator and its denominator. If \, m \, is the greatest common factor of the polynomials \, p \, and \, q , that is if \, m = \mathrm{gcf}(p,q) , then the polynomial fraction \, \frac{\frac{p}{m}}{\frac{q}{m}} \, is called maximally reduced or irreducible.
No further reduction is possible since the nominator and the denominator of this polynomial fraction have no common factor greater than one, that is we have \, \mathrm{gcf}(\frac{p}{m},\frac{q}{m}) = 1 . Two such polynomials are called coprime, relatively prime or mutually prime.
///////