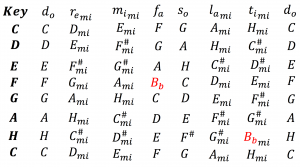This page is a sub-page of our page on Music.
////////
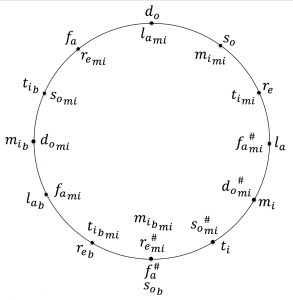
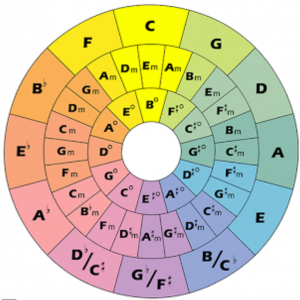
The abstract quint circle:
\, {s_o}^0 = d_o = 2^{ \, \frac{0}{12}} .
\, {s_o}^1 = s_o = 2^{ \, \frac{0}{12}} \, 2^{ \, \frac{7}{12}} = 2^{ \, (\frac{0}{12} + \frac{7}{12})} = 2^{ \, \frac{7}{12}} .
\, {s_o}^2 = r_e = 2^{ \, \frac{7}{12}} \, 2^{ \, \frac{7}{12}} = 2^{ \, (\frac{7}{12} + \frac{7}{12})} = 2^{ \, \frac{14}{12}} = 2^{ \, \frac{2}{12}} .
\, {s_o}^3 = l_a = 2^{ \, \frac{2}{12}} \, 2^{ \, \frac{7}{12}} = 2^{ \, (\frac{2}{12} + \frac{7}{12})} = 2^{ \, \frac{9}{12}} .
\, {s_o}^4 = m_i = 2^{ \, \frac{9}{12}} \, 2^{ \, \frac{7}{12}} = 2^{ \, (\frac{9}{12} + \frac{7}{12})} = 2^{ \, \frac{16}{12}} = 2^{ \, \frac{4}{12}} .
\, {s_o}^5 = t_i = 2^{ \, \frac{4}{12}} \, 2^{ \, \frac{7}{12}} = 2^{ \, (\frac{4}{12} + \frac{7}{12})} = 2^{ \, \frac{11}{12}} .
\, {s_o}^6 = \hat{f_a} = 2^{ \, \frac{11}{12}} \, 2^{ \, \frac{7}{12}} = 2^{ \, (\frac{11}{12} + \frac{7}{12})} = 2^{ \, \frac{18}{12}} = 2^{ \, \frac{6}{12}} .
\, {s_o}^7 = \hat{d_o} = 2^{ \, \frac{6}{12}} \, 2^{ \, \frac{7}{12}} = 2^{ \, (\frac{6}{12} + \frac{7}{12})} = 2^{ \, \frac{13}{12}} = 2^{ \, \frac{1}{12}} .
\, {s_o}^8 = \hat{s_o} = 2^{ \, \frac{1}{12}} \, 2^{ \, \frac{7}{12}} = 2^{ \, (\frac{1}{12} + \frac{7}{12})} = 2^{ \, \frac{8}{12}} .
\, {s_o}^9 = \hat{r_e} = 2^{ \, \frac{8}{12}} \, 2^{ \, \frac{7}{12}} = 2^{ \, (\frac{8}{12} + \frac{7}{12})} = 2^{ \, \frac{15}{12}} = 2^{ \, \frac{3}{12}} .
\, {s_o}^{10} = t_{i_b} = 2^{ \, \frac{3}{12}} \, 2^{ \, \frac{7}{12}} = 2^{ \, (\frac{3}{12} + \frac{7}{12})} = 2^{ \, \frac{10}{12}} .
\, {s_o}^{11} = f_a = 2^{ \, \frac{10}{12}} \, 2^{ \, \frac{7}{12}} = 2^{ \, (\frac{10}{12} + \frac{7}{12})} = 2^{ \, \frac{17}{12}} = 2^{ \, \frac{5}{12}} .
\, {s_o}^{12} = d_o = 2^{ \, \frac{5}{12}} \, 2^{ \, \frac{7}{12}} = 2^{ \, (\frac{5}{12} + \frac{7}{12})} = 2^{ \, \frac{12}{12}} = 2^{ \, \frac{0}{12}} .
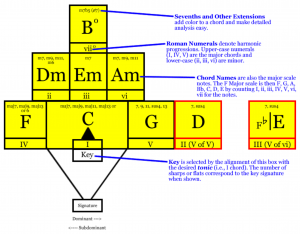
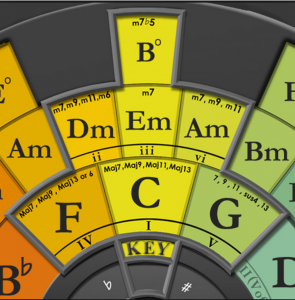
/////// Chords:
/////
/////
/////
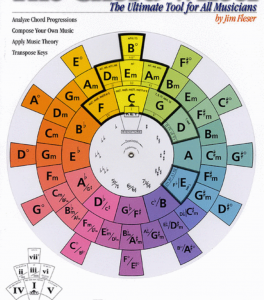
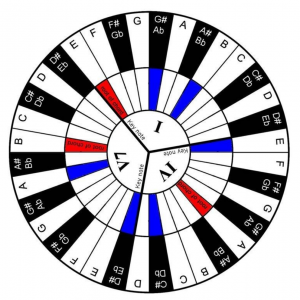
A chord wheel for piano (Structurally, this is a slide rule “wrapped around three octaves”):
/////
/////
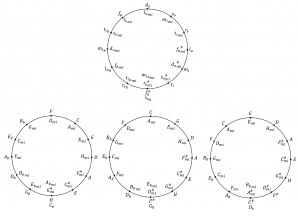
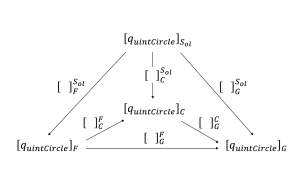
The abstract quint circle and its instantiations in \, d_o := F, \, d_o := C, \, \text {and} \, d_o := G \, :
A quint-circle transposition diagram:
