This page is a sub-page of our page on Linear Transformations.
///////
Related KMR pages
• Representation and Reconstruction of Vectors.
• Representation and Reconstruction of Linear Transformations.
• The Rank-Nullity theorem
///////
The interactive simulations on this page can be navigated with the Free Viewer
of the Graphing Calculator.
///////
Setting up a Linear Space Probe for visual exploration of linear transformations
1. Introduce a set of parallel and equidistant planes parametrized by the direction of their shortest distances to the origin. This direction is the same for every such plane. Moreover, let one of these planes pass through the origin. We will call this plane the centre plane.
2. For each plane in this set, introduce a line that lies in this plane and passes through its point of shortest distance to the origin. Since the centre plane passes through the origin, so will the line that lies in this plane. We will call this line the centre line. (In the films below, the centre plane is depicted in grey and the centre line is depicted in red).
3. Make sure that the centre plane can rotate around the centre line and let the other planes move in such a way that they maintain their parallelity to the centre plane. Since the points of shortest distance to the origin change, the lines will be recalculated, but, because the centre line is invariant, the lines will retain a fixed point of intersection at infinity and therefore they will also retain their parallelity in relation to each other.
4. Make sure that the centre line can rotate in the centre plane around its point of shortest distance to the origin, i.e., the origin itself. Let each of the other lines rotate around its respective point of shortest distance to the origin in such a way that it maintains its parallelity with the rotating centre line.
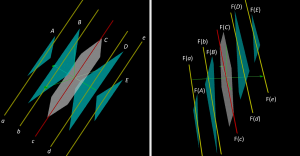
The left part of this figure illustrates the construction. The parallel planes are called \, A, B, C, D, \, and \, E \, and the lines are called \, a, b, c, d, \, and \, e . The line \, a \, lies in the plane \, A , the line \, b \, lies in the plane \, B , the line \, c \, lies in the plane \, C , the line \, d \, lies in the plane \, D , and the line \, e \, lies in the plane \, E . The plane \, C \, is the centre plane (depicted in grey) and the line \, c \, is the centre line (depicted in red). The centre plane \, C \, and the centre line \, c \, are the only lines and planes of the space probe that form linear subspaces of \, \mathbb {R^3} \, . The rest of the planes (depicted in light-blue) and lines (depicted in yellow) form affine subspaces of \, \mathbb {R^3} \, .
/////// Quoting Wikipedia on affine geometry (2018-09-21):
Affine geometry can […] be developed on the basis of linear algebra. In this context an affine space is a set of points equipped with a set of bijective transformations called translations, which forms a vector space (over a given field, commonly the real numbers), and such that for any given ordered pair of points there is a unique translation sending the first point to the second; the composition of two translations is their sum in the vector space of the translations.
In more concrete terms, this amounts to having an operation that associates to any ordered pair of points a vector and another operation that allows translation of a point by a vector to give another point; these operations are required to satisfy a number of axioms (notably that two successive translations have the effect of translation by the sum vector). By choosing any point as “origin”, the points are in one-to-one correspondence with the vectors, but there is no preferred choice for the origin; thus an affine space may be viewed as obtained from its associated vector space by “forgetting” the origin (zero vector).
/////// End of quote from Wikipedia.
Hence, in affine geometry, a vector \, A \, is in fact a displacement vector which defines a rectilinear displacement (= a translation) \, \overrightarrow {x ,A x} \, between the points \, x \, and \, A x .
By choosing any point \, O \, as the origin, the set of translations \, V_O = \{ \, \overrightarrow{O,x} : x \in X \, \} \, forms a vector space, and we have for each pair of points \, x, y \in X \, :
\, \overrightarrow{O,x} + \overrightarrow{O,y} = \overrightarrow{O,x+y} ,
\, \overrightarrow{O,y} = \overrightarrow{O,x} + \overrightarrow{x,y} = \overrightarrow{O,x} + \overrightarrow{O,y-x} ,
\, \overrightarrow{x,y} = \overrightarrow{O,y} - \overrightarrow{O,x} = \overrightarrow{O,y-x} .
Two points \, a \, and \, b \, in \, X \, span an affine subspace of dimension one,
which is called an affine line. In \, V_O \, this line can be parametrised as
\, \{ \lambda \, \overrightarrow{O,a} + (1-\lambda) \, \overrightarrow{O,b} : \lambda \in \mathbf {R} \} .
The difference between two displacement vectors is called a direction vector (or a Euclidean vector). The direction vector \, a - b \, spans a linear subspace that is parallel to the affine subspace spanned by the displacement vectors \, a \, and \, b \, .
Hence, for the linear space probe we can say that:
• if the tips of two displacement vectors lie on the same yellow line,
then the direction vector of their difference lies in the red centre line.
• if the tips of two or more displacement vectors lie on the same light-blue plane,
then the direction vectors of their pairwise differences lie in the grey centre plane.
Geometrically, the take-away lesson from this discussion is that:
• A displacement vector represents a change of position called a translation.
• A direction vector represents a change of direction. The magnitude of the direction vector corresponds to the magnitude of the directional change that it represents.
• The difference between two displacement vectors is a direction vector.
• The affine subspace spanned by a finite number of displacement vectors is parallel to the linear subspace spanned by the direction vectors of their pairwise differences.