This page is a sub-page of our page on Category Theory.
///////
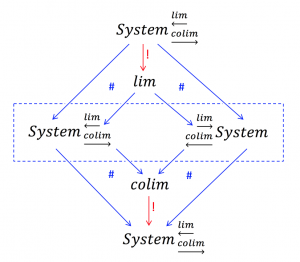
Limit and Colimit of a System:
///////
Examples:
///////
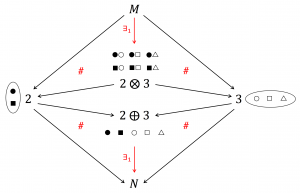
Product and coproduct of 2 and 3 in the category \, \mathbf{S_{ets}} \, :
///////
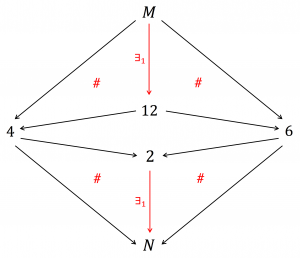
Product and coproduct of 4 and 6 in the “divisor” category \, \langle \, {\mathbb {N}}^+ \, | \, \rangle \,
(where there is an arrow from every positive natural number to each of its divisors):
///////
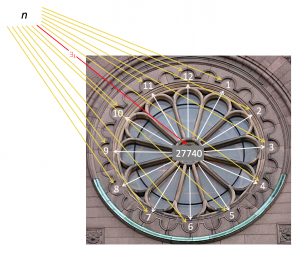
The universal property of the lcm of a finite set of \, n_{umbers} \in {\mathbb {N}}^+ \, :
The least common multiple (lcm) of the numbers \, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 \,
is \, 27740 . Hence, every natural number \, n \geq 1 \, that is divisible by all of the numbers \, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 \, must be divisible by \, 27740 , which is indicated by the red arrow in the diagram. The uniqueness of this arrow is obvious since there is at most one arrow between any two numbers \, m \, and \, n \, , an arrow being present if and only if \, m \, divides \, n \, or vice versa.
Hence, the limit of a finite set of positive natural numbers
in the divisor category
is given by their least common multiple.
For more on the divisor category, see Category of natural numbers with divisbility which describes the op-category of \, \langle \, {\mathbb {N}}^+ \, | \, \rangle , that is the category that arises from \, \langle \, {\mathbb {N}}^+ \, | \, \rangle by reversing the direction of each of its arrows.
• Hasse Diagram (at Wikipedia)
• Hasse Diagrams of integer Divisors
(at http://demonstrations.wolfram.com/HasseDiagramsOfIntegerDivisors/)
///////
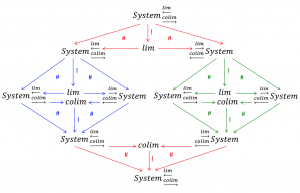
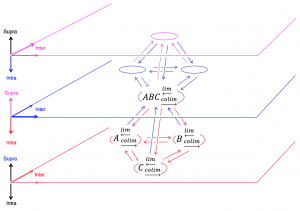
The recursive character of the limit and colimit of systems:
///////
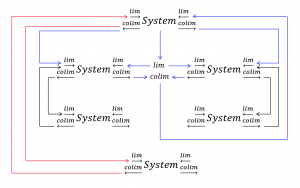
Another layout of hierarchic limits and colimits:
///////
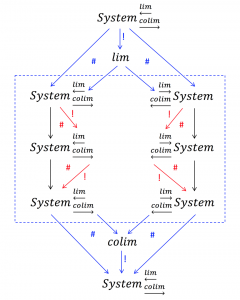
Yet another layut of hierarchic limits and colimits:
///////
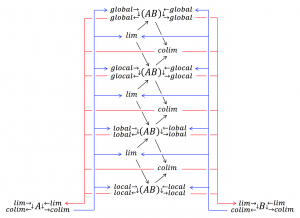
Local, lobal, glocal, global limits and colimits:
///////
Bottom-up organization:
///////