This page is a sub-page of our page on Basic properties of functions.
///////
The sub-pages of this page are:
• …
///////
Related KMR-pages:
• Topology
///////
Other relevant sources of information:
• Norm
• Topology
• Metric
• Continuity in mathematics
The interactive simulations on this page can be navigated with the Free Viewer
of the Graphing Calculator.
///////
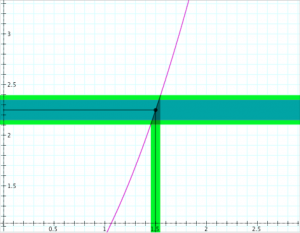
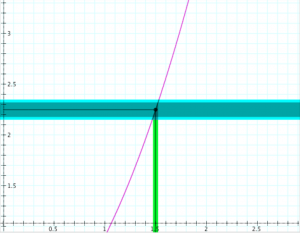
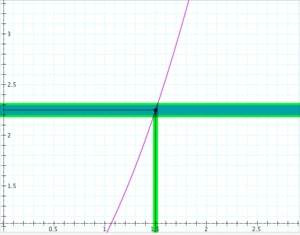
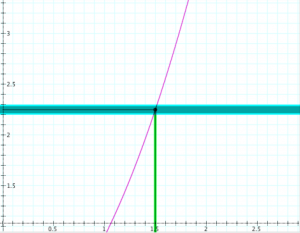
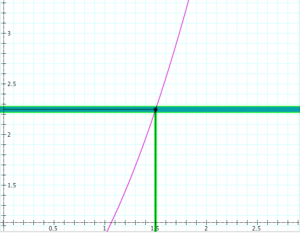
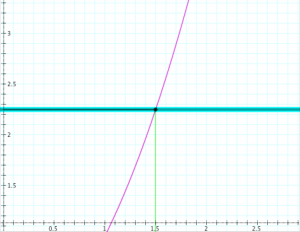
Continuity at a point (the metric “epsilon-delta” definition):
Definition: The function \, f : \mathbb{R} \rightarrow \mathbb{R} \, is continuous at the point \, x = x_0
if, for each \, \epsilon > 0 , there is a \, \delta > 0 \,
such that \, |f(x) - f(x_0)| < \epsilon \, if \, |x - x_0| < \delta .
///////
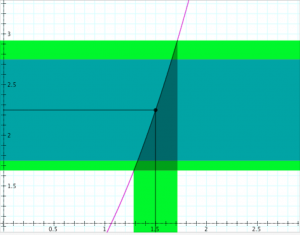
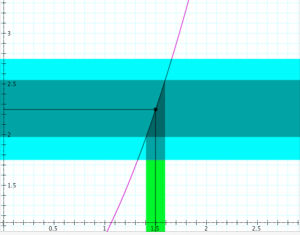
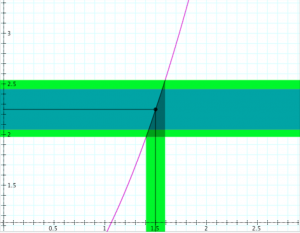
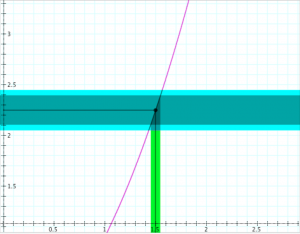
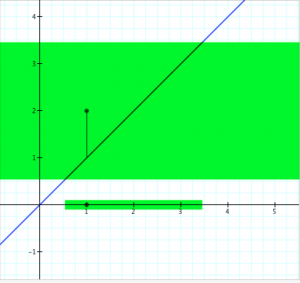
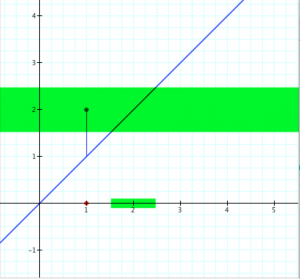
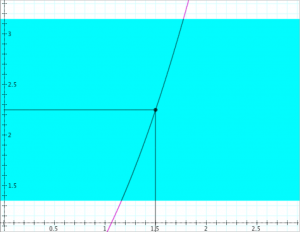
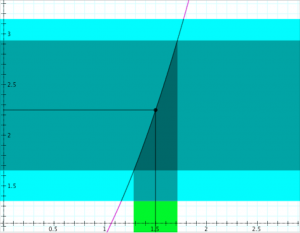
Determining continuity at a point (the “epsilon-delta trial”):
Determining the continuity of the function \, y = f(x) \, at the point \, x = x_0 .
If \, \delta \, ‘wins’, i.e., if there is a \, \delta > 0 \, for each \, \epsilon > 0,
then the function \, f(x) \, is continuous at the point \, x_0 .
If \, \epsilon \, ‘wins’, i.e., if there is an \, \epsilon > 0 \, for which there is no \, \delta > 0 \, ,
then the function \, f(x) \, is discontinuous at the point \, x_0 .
In the diagrams below, the vertical interval \, |f(x) - f(x_0)| < \epsilon \, is depicted in blue, and the horizontal interval \, |x - x_0| < \delta \, (and its corresponding vertical interval) is depicted in green.
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; Choosing \, \epsilon \, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; Choosing \, \delta \,
///////
A topology provides a definition of open sets
A topological space is a set endowed with a structure, called a topology, which allows defining continuous deformation of subspaces, and, more generally, of all kinds of continuity.
/// TEXT HERE
A topological space is, roughly speaking, a geometrical space in which closeness is defined but, generally, cannot be measured by a numeric distance. More specifically, a topological space is a set of points, along with a set of neighbourhoods for each point, satisfying a set of axioms relating points and neighborhoods.
A topological space is the most general type of a mathematical space that allows for the definition of limits, continuity, and connectedness. Other spaces, such as Euclidean spaces, metric spaces and manifolds, are topological spaces with extra structures, properties or constraints. Euclidean spaces, and, more generally, metric spaces are examples of a topological space, as any distance or metric defines a topology.
On the real axis \, \mathbb{R} \, , the open sets consist of unions and finite intersections of open intervals.
///////
The topological definition of continuity at a point:
The pullback (= the preimage) of open sets are open.
The interactive simulation that created this movie.
///////
Uniform continuity on an interval:
Definition: The function \, f : \mathbb{R} \rightarrow \mathbb{R} \, is uniformly continuous on the interval \, [a,b]
if, for each \, \epsilon > 0 , there is a \, \delta > 0 \, such that \, |f(x) - f(x + \delta)| < \epsilon \, if \, x \in [a,b] . ///////
///////