This page is a sub-page of our page on Discourse Algebra.
///////
Related KMR pages:
• Matrix Algebra
• The Pseudoinverse of a linear map
///////
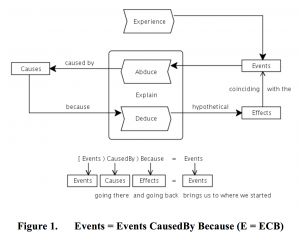
1. A plausible explanation as an abductive pseudoinverse
Describing a plausible explanation as an abductive pseudoinverse involves finding the “most likely” (≈ “least distorting”) explanation of a series of events.
1.1. The concept of pseudoinverse
In mathematics, an inverse mapping that results from such a minimal distortion of the context is called a pseudoinverse. Pseudoinverses are constantly appearing in numerical computations, since the systems of equations that one wants to solve are over-determined and therefore, in general, they have no solutions as they stand.
In philosophy, looking for causes to explain the appearance of events as effects of these causes is known as abductive reasoning. Hence we can describe the creation of a plausible explanation for a series of events as the creation of an abductive pseudoinverse, which means finding the “most plausible” explanation of this series of events in terms of semantic proximity.
/////// Explore the analogy with interpolating between n points using a polynomial of the lowest possible degree. The lower the degree the more plausible the explanation. This is consistent with Newton’s principle as formulated in his Principia Mathematica: “We shall not assume more causes for the observed phenomena than is necessary to explain them.” [Check Ref]
/////// Explore the connections with Algorithmic Information Theory.
/////// Quoting from Gregory Chaitin, Meta Math (p.62):
Okay, it’s time to look at Leibniz’s Discourse on Metaphysics! Modern science was really just beginning then. And the question that Leibniz raises is, how can we tell the difference between a world that is governed by law – one in which science can apply – and a lawless world? How can we decide if science actually works? In other words how can we distinguish between a set of observations that obeys a mathematical law and one that doesn’t?
And to make the question sharper, Leibniz asks us to think about scattering points at random on a sheet of paper, by closing our eyes and stabbing at it with a pen many times. Even then, observes Leibniz, there will always be a mathematical law that passes through those very points. [… Lagrangian interpolation].
That seems very discouraging. How can we decide if the universe is capricious or if science actually works? And here is Leibniz’s answer: If the law has to be extremely complicated (“fort composée”) then the points are placed at random, they’re “irrégulier,” not in accordance with a scientific law. But if the law is simple, then it’s a genuine law of nature, we’re not fooling ourselves!
See for yourself; look at Sections V and VI of the Discourse.
The way that Leibniz summarizes his view of what precisely it is that makes the scientific enterprise possible is this: “God has chosen that which is the most perfect, that is to say, in which at the same time the hypotheses are as simple as possible, and the phenomena are as rich as possible.” The job of the scientist, of course, is then to figure out these simplest possible hypotheses.
/////// End of quote from Gregory Chaitin
An explanation of ‘what happened’ can be seen as an attempt to create an inverse mapping from effects to causes and effects. Since the causes are (at least partially) hidden, and since many causes can give rise to the same effect, such an inverse mapping is not possible to create. What can be done is to create a plausible explanation, which means an explanation that distorts the semantics of the context as little as possible. To measure such minimal semantic distortions one must have a measure of semantic proximity on the (Cause, Effect) space.
1.2. An explanation/interpretation as an abductive pseudoinverse
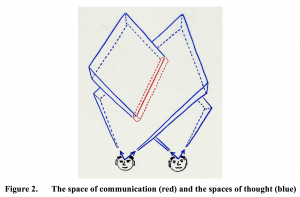
Figure 2 depicts two cognitive systems (individuals) involved in communication. Each individual has his own thought space (blue) and a shared space of communication (red).
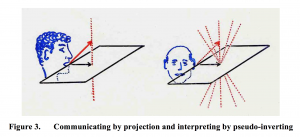
Figure 3 shows an example of an exchange of thoughts between these individuals, or, rather a mapping of a thought in the head of the individual to the left (the sender), via a message that he expresses in the communication space, to a thought that is created in the head of the individual to the right (the receiver).
This mapping process takes place in two steps. In the first step, the initial thought of the sender is projected into a message in communication space, and in the second step this message is picked up by the receiver and interpreted as a thought in the receiver’s own thought space.
In the first step, the thought of the sender can be regarded as the cause, and the expressed message in communication space is the effect of this cause.
In the second step, the receiver tries to reconstruct the meaning that the sender expressed by this message, or rather what the receiver thinks that the sender meant by his expressed message. This can be seen as an attempt to create an inverse mapping from the effects (messages) to the causes (= ideas) behind the messages.
Since the causes are (at least partially) hidden, and since many causes can give rise to the same effect, such an inverse mapping is not mathematically possible to create. What the receiver can aim for is to try to find the idea in his own thought space that is the most plausible explanation of the received message.
This corresponds to an idea in the receiver’s thought space that explains the received message in a way that distorts its meaning (= semantics) as little as possible. To measure such minimal semantic distortions one must have a measure of semantic proximity on the (Cause, Effect) space.