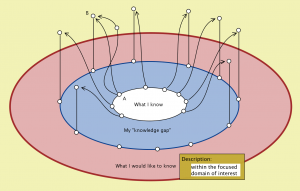
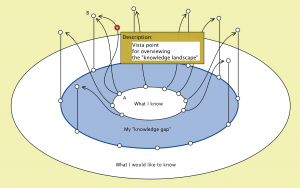
Self-Empowered Community Initiative for Augmented Social Resilience
This page is a sub-page of our page on Humanity Inc.
///////
Books:
• The Deficit Myth: Modern Monetary Theory and How to Build a Better Economy,
by Stephanie Kelton, John Murray Publishers, 2020.
• Moral capitalism: Why Fairness Won’t Make Us Poor, by Steven Pearlstein, St. Martin’s Griffin, 2020 (2018).
/////// Stubs for the text:
• The Big Switch
• Humanity Inc.
• Robinson Rescue
• MATCH
• Algebra
• Knowledge Algebra
• Disagreement Management
• Knowledge Negotiations
• Collectigence
• Words ∆ Deeds
• Bringing back the initial vision of the web (using Erik’s infrastructure)
• From catalogic (= top-down) to analogic (= bottom-up) connection of semantic information
• The conzilloscope
• From Emotional Opiniocracy to Reasonable Visionocracy
• From Graph theory to Category Theory
• CHARGE (Cultural Heritage Asynchronous Research Grid Environment)
• MATCH (MAthematical Transformations for Cultural Heritage)
• Creating lack of liability by blaming others
• The Corporation – the pathological pursuit of profit and power
• Permission to Steal: Revealing the Roots of Corporate Scandal
• The humanisation of globalisation
• The nEUrotic economy – finance without resistance
• The Small-Mart Revolution
///////
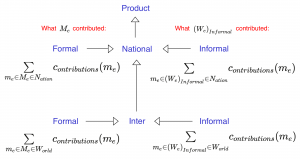
Social Algebra:
Formal and Informal National and International Products:
///////
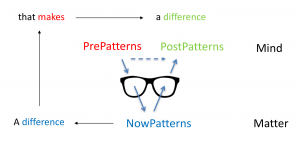
Bioentropy and Gregory Bateson:
“Information is a difference that makes a difference”:
///////
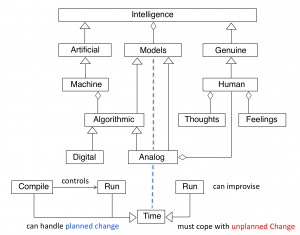
Artificial Ethics:
Artificial versus Genuine Intelligence:
///////
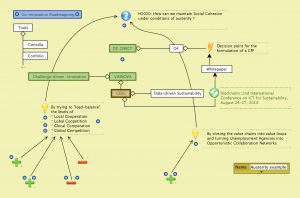
Influence map for Horizon 2020
Austerity example:
///////
\, \left< \, W_{orkers} \, \right| \left| \, S_{kills} \, \right> \, \left< \, S_{kills} \, \right| \left| \, J_{obs} \, \right> \, :
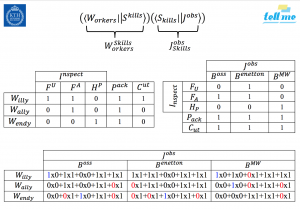
Who will be able to do which jobs with what training:
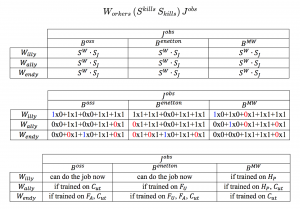
///////
Business Algebra:
The Ericsson AXE10 delay:
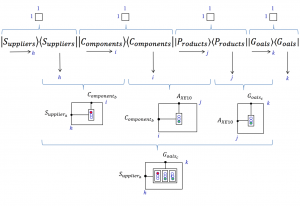
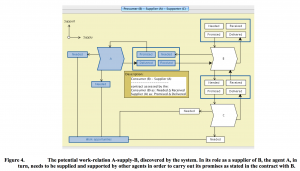
This figure shows the top-level Ericsson supply chain product as a formal matrix product of traffic lights, each one dynamically controlled by some form of change management process.
In this way a company can have dynamic control over each separate path and manage its interactions with others more effectively and efficiently. As described above, one of the components, called \, {C_{omponent}}_b \, in the figure, of the (at that time) soon-to-be-released switchboard was red-flagged for delay by the corresponding supplier, called \, {S_{upplier}}_a \, . This red flag is reflected in the switch to red of the left-most factor of the sequence of traffic lights displayed at the bottom of the figure.
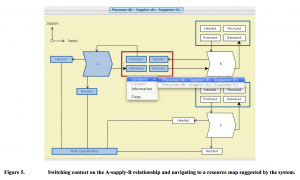
The figure below shows the matrix product of the three relational matrices
\, \left< \, {S_{upplier}}_a \, \right| \left| \, {C_{omponent}}_b \, \right> \, \left< \, {C_{omponent}}_b \, \right| \left| A_{XE10} \, \right> \, \left< \, A_{XE10} \, \right| \left| \, {G_{oal}}_c \, \right> \,
at the next level of detail. The traffic lights have been expanded to state diagrams that model not only that – but also under what conditions – the switch from green to red is occurring.
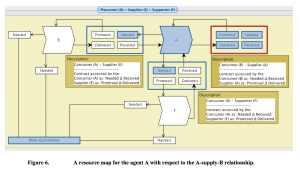
The next-to-top level diagram product of the problematic supply chain path:
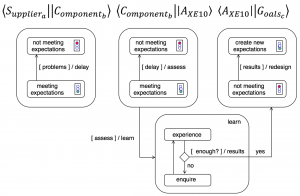
As seen in this figure, the dynamic interactions are handled by message passing
between state diagrams in accordance with the Unified Modeling Language.
///////
Business Algebra: Dynamic Employment Agency
Dynamic employment agency 2:
A vacancy in job \, J_1 \, at company \, C^p \, :

Dynamic employment agency 3:
h new workers, q new skills, r new jobs, s new companies:
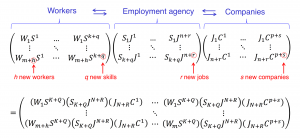
Dynamic employment agency 4:
Skills vector refinement of job \, J_j \, at company \, C^i \, :
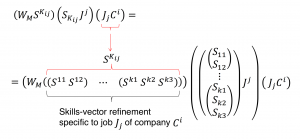
///////
Electronic Commerce Integration Meta Framework:
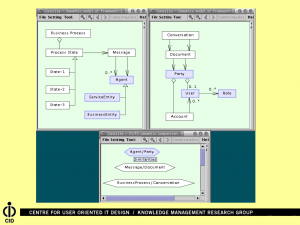
///////
Ethical E-Commerce:
Taxonomy of value types:
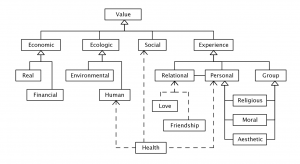
///////
The Opportunistic Collaboration Agency:
///////
The Mathematical Explainatorium:
Changing your attitude to mathematics:
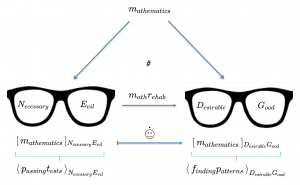
///////
///////
What is mathematics?
Newton and Einstein firing a pistol on a train:
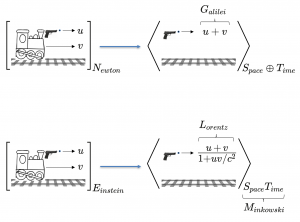
Mathematics is representation:
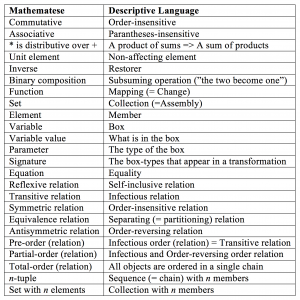
From Mathematese to Descriptive Language:
///////
First Class Mathematics aims to convey an image of mathematics as a double-brained mental activity. In order to develop the ability for structural thinking, it is of the utmost importance that all students are encouraged and supported in their attempts to develop their own mathematical fantasies during their entire learning process. This is only possible if they are confronted with interesting examples of ‘good mathematics’ during every stage of their mathematical education process.
An illustrative example of the effects of such a confrontation is given by the so called Rubrik’s cube (known simply as “the cube“), which was such a fascinating mental torment to the kids in the 1980s. They got into doing their own advanced forms of algorithmic mathematics – but only during their breaks and time of leisure from a school-system that was totally incapable to realize what was going on, let alone to make use of it in order to promote the mathematical interest of the students. Our electronic portfolio archive on First Class Mathematics can be found here.
By the aid of modern computers, many exiting mathematical structures can be animated and brought to interactive life in ways that open new and exiting didactic possibilities. Today there is a large number of computer-based mathematical tools that empower a student to explore mathematical concepts in interactive and dialectical ways, i.e. in an ongoing dialogue with the computer program (and of course with the teacher). It is the aim of the First Class Mathematics project to contribute to the developments of such tools, as well as to promote a didactic strategy that makes it possible to integrate them in the educational process in a way that stimulates interest to learn more about the underlying mathematical structures.
An example of how “first class math rehab” can be carried out in practice is presented here.
///////
Experiment here with different arithmetic operations.
Whenever you feel like it, you are invited to try out a ring of characteristc different from zero, and investigate what happens. Can you figure out what is going on here? In mathematese ( = the language of mathematics) we call it modular arithmetic and it obeys the rule:
x+n \times a \equiv x \pmod a , \forall \, x, n, a \in \mathbb {Z}.
What this rule means (in plain English) is that the integers x and x + n \times a
have the same remainder when you divide them by the integer a.
Modular Arithmetic Visually Explained
(Zach Star on YouTube):
///////
Experiment here with the mathematical cogwheels. You will be able to verify that:
• The number of pairs that are output in each complete run of the wheels
is precisely lcm (m, n) = the least common multiple of the numbers m and n.
• The number of times that the start position of the left wheel has to be changed in order to generate all possible combinations (= pairs) of the two numbers
is precisely gcf (m, n) = the greatest common factor of the numbers m and n.
Here is a pictorial description of these facts.
The Mathematical Cogwheels provide a way to experience the ‘action’ (= effect) of these important concepts ( lcm and gcf ) without having to talk about them explicitly. This direct cognitive experience of the actions of the concepts involved makes it possible to give the students a chance to describe the resulting structures as they experience them in a first encounter, without introducing the definitions of the underlying concepts in advance.
Hence it becomes possible to engage the students in the crucially important activity of mathematics design, by encouraging them to represent the structures that they experience in a way that is as effective and efficient as possible.
This represents a form of “mathematical didactics” that is based on:
• providing cognitive contact with the underlying mathematical structures, and
• representing these structures in an increasingly effective and efficient manner.
///////
Story-scripts/maps for three different hikes:
1) From Numbers, via Music, to Vectors and Linear Transformations.
2) From Numbers, via Music and Vectors, and Linear Transformations to Category Theory.
3) From Conics and Quadrics, via Projective Geometry, Projective Metrics
and Non-Euclidean Geometry, to Einstein’s Special Theory of Relativity.
Hike 2) is an expansion of hike 1). However, a “birds-eye view” of Category Theory should be introduced also in hike 1) as a kind of “vista point” since Category Theory provides a structural framework that unifies an amazingly large number of different mathematical concepts and constructions (including Numbers, Vectors, and Musical Notation).
The overall idea is that structures, constructions, concepts, … are difficult to understand unless one is able to modify them in a controlled way. A point of entry into the subject of changing the background of a representation can be found at our page on Shift of Basis.
Eleven stories designed to raise interest in mathematics
1. The story of the people who thought the world was understandable.
From Thales and Pythagoras to Democritus and Aristarkos.
2. The story of the people that wanted to escape the realm of the senses.
From Plato via Augustine and Aquino to the age of scholasticism.
3. The mathematics of the eye: The development of true perspective.
From Pappus via della Franchesca and da Vinci to Desargues, Pascal, Poncelét, Plücker, Grassmann and Klein.
4. Einstein for Flatlanders: Two-dimensional relativity theory.
The story about the flatlanders that lived on a sphere and the flatlanders that lived on a torus (“dough-nut”).
5. The story of the people that disregarded almost everything.
The evolution of abstract thinking: From induction and abduction to abstraction and deduction. “The power of thinking is knowing what not to think about.”
6. On the difficulties of overcoming psychological complexes.
The story about the development of the concept of number: From “positive” or “natural” to “negative”, from “rational” to “irrational”, from “real” to “imaginary” and “complex”.
7. What is there between the atoms?
Does the world consist of particles or waves – or maybe something else? The historical debate from Thales versus Pythagoras via Newton versus Huygens to Einstein versus Bohr and Heisenberg and the break-up of the particle concept through the emergence of string theory and superstring theory.
8. The mysterious law about the degradation of work:
The principles of energy and entropy. The development of the energy concept from Leibniz via Count Rumford and Carnot to Mayer, Joule and Boltzmann.
9. The story of the long-lived demon that was unable to forget.
Maxwell’s demon and the deep connections between information theory and thermodynamics.
10. The evolution of geometric arithmetic.
11. Linear Algebra: The story of the linear war
between the planets Vectoria and Vectoria’.
///////
Social Algebra and Social Calculus:
Opportunity mining and Innovation response:
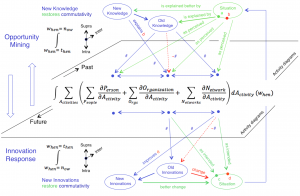
Social Algebra and Social Calculus:
The TELLME Innovation cycle:
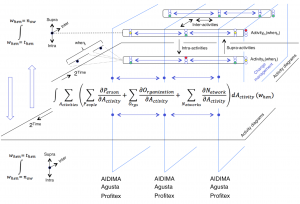
///////
///////
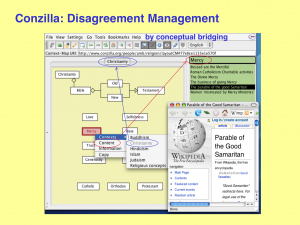
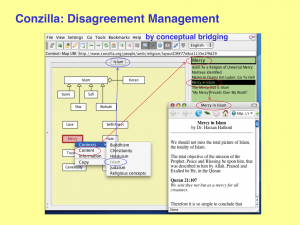
Conzilla: Disagreement management
by conceptual bridging:
///////
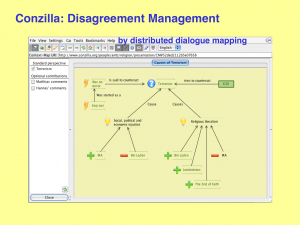
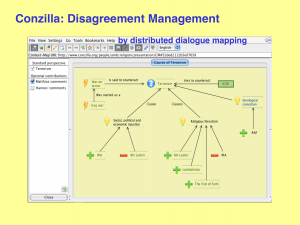
Conzilla: Disagreement management
by distributed dialogue mapping:
///////
Local, Lobal, Glocal and Global networks surrounding a Town:
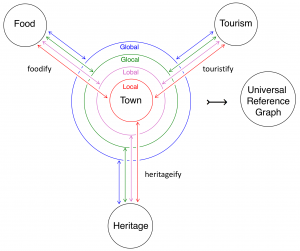
///////
Limits and Colimits:
Two agents A and B interacting at different levels:
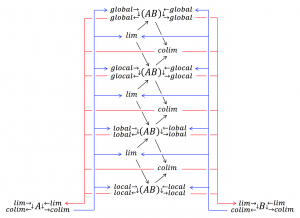
///////
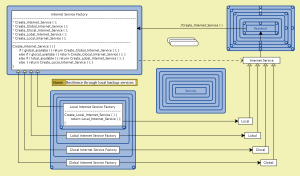
Resilience through global/glocal/lobal/local backup services:
///////
Conceptopedia:
A global concept improvement process:

///////
Knowledge Algebra:
Monitoring and connecting through chains of knowlecules:

///////
Interpreting objects through concepts:
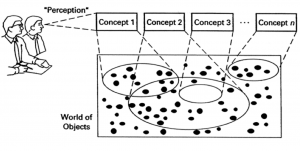
///////
MATCH:
The advantage of stable abstractions:
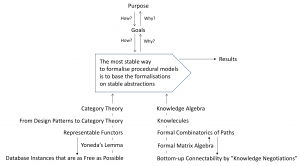
///////
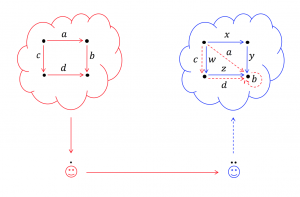
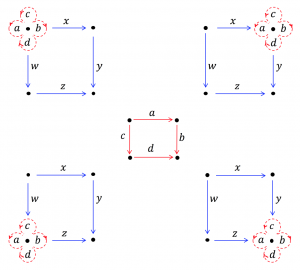
Category Theory:
Functor mapping between two knowlecules
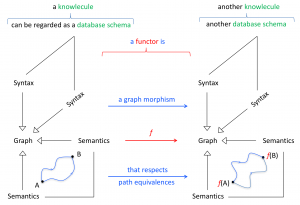
///////
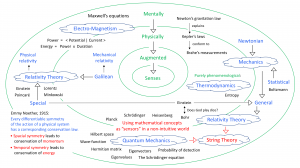
Physically and mentally augmented senses:
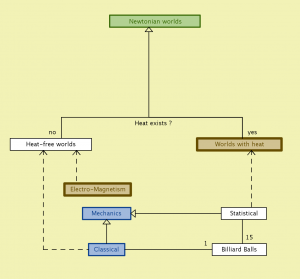
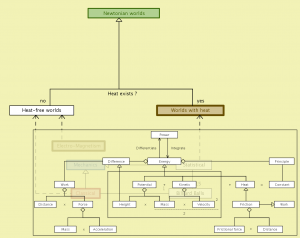
Newtonian worlds – peeking into Classical Mechanics:
Newtonian worlds – peeking into worlds with heat:
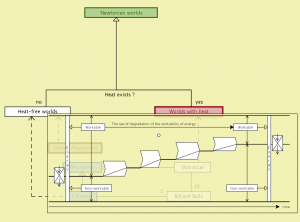
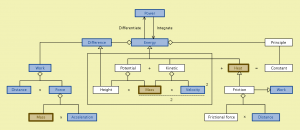
Worlds with heat – the decreasing workpower of energy:
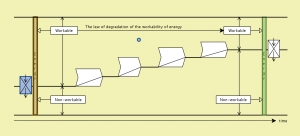
The Entropy Law and the Economic Process:
///////
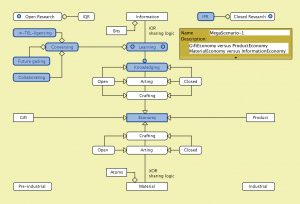
MegaScenario:
Gift Economy versus Product Economy and
Information Economy versus Material Economy:
Peeking into the TEL-Map observatory:
///////
The TEL-Map observatory:
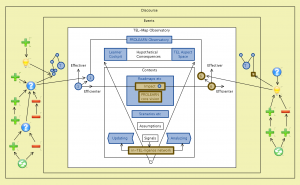
The TEL-Map observatory:
Peeking into the in-TEL-ligence network:
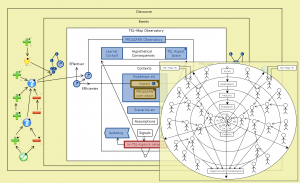
The TEL-Map observatory:
Peeking into the Learner Cockpit:
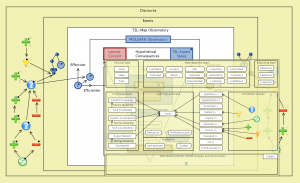
///////
Storytelling:
Functorial and non-functorial patterns:

///////
The Human Category:
What we agree on and what we obey:
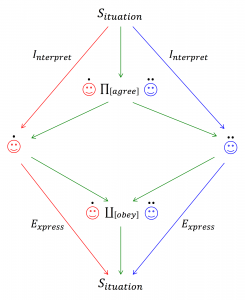
///////
The Human Category:
Communicating through thought-graphs:
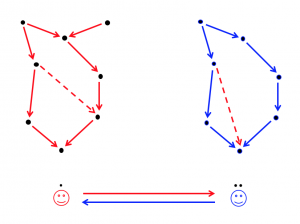
///////
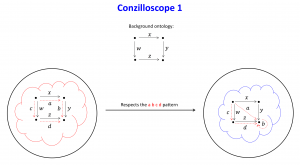
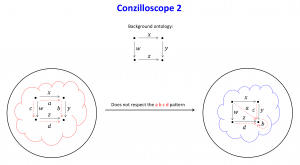
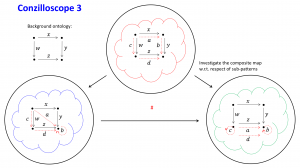
Conzilla:
The Conzilloscope:
///////
Tertionary Hypergraphs:
Who says what and why?
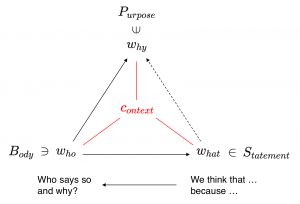
///////
Robinson rescue modeling
Insiders learn how to speak “outside-speak”
in order to help formulate inside needs
and develop the appropriate skills
to satisfy these needs, and
advertise their acquired skills to the outside
in order to help others with similar needs.
///////
A conversational feedback loop in Knowledge Loop Algebra
between the communities \, A \, and \, B \, using the \, O_{utside} \, communication protocol :
\, \overbrace{\langle \, {O_{utside}}^U \, \vert \vert \, {I_{nside}}^A \, \rangle}^{\text{select}} \overbrace{\langle \, {I_{nside}}^A \, \vert \vert \, {S_{tart}}^A \, \rangle}^{\text{initialize}} \overbrace{\langle \, {M_0}^A \, \vert \, \cdots \, \vert \, {M_{m_1}}^A \, \rangle}^{\text{solve}} \overbrace{\langle \, {R_{esults}}^A \, \vert \vert \, {O_{utside}}^U \, \rangle}^{\text{advertise}} \,
\, \langle \, {O_{utside}}^A \, \vert \vert \, {I_{nside}}^B \, \rangle \langle \, {I_{nside}}^B \, \vert \vert \, {S_{tart}}^B \, \rangle \langle \, {M_0}^B \, \vert \, \cdots \, \vert \, {M_{n_1}}^B \, \rangle \langle \, {R_{esults}}^B \, \vert \vert \, {O_{utside}}^U \, \rangle \,
\, \langle \, {O_{utside}}^B \, \vert \vert \, {I_{nside}}^A \, \rangle \langle \, {I_{nside}}^A \, \vert \vert \, {S_{tart}}^A \, \rangle \langle \, {M_0}^A \, \vert \, \cdots \, \vert \, {M_{m_2}}^A \, \rangle \langle \, {R_{esults}}^A \, \vert \vert \, {O_{utside}}^U \, \rangle \,
///////
///////
///////
///////
///////
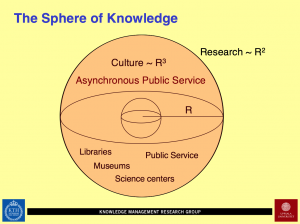
Asynchronous Public Service and CHARGE
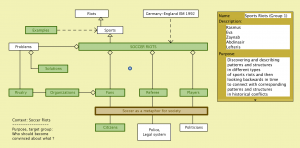
NSDL-1 Sports Riots group (Workshop 1):
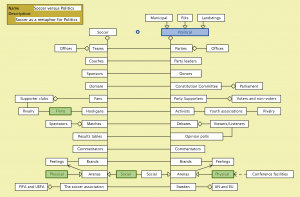
NSDL-1 Sports Riots group (Workshop 2):
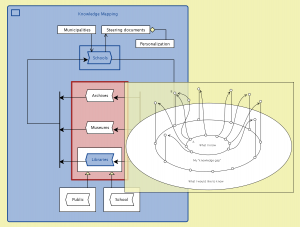
NSDL – Next Phase: Knowledge Modeling and Mapping
for Collaboration between Schools and Heritage Institutions:
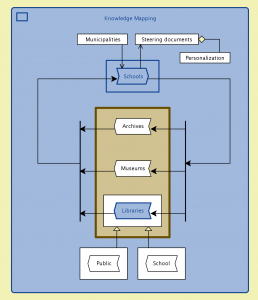
///////
References:
• Naeve, A., (2010) Opportunistic (L)earning in the Mobile Knowledge Society, IJMBL, 2(4), 2010, Special Issue on Mobile Learning in the Context of Transformation.
• Naeve, A., (2011) A Modeling Primary on Communicative Modeling and Disagreement Management. TEL-Map Deliverable D1.1, January 2011.
• The Big Switch
• TELLME-D1.3-Annex(v2).docx
Business Algebra: A Mathematical Framework for Business Process Modeling
• Knowledge Algebra
• From catalogic (= top-down) to analogic (= bottom-up) connection of semantic information (Conzilla and Confolio)
Humanity Incooperated:
Capturing and supporting collaborations
that practice small & smart cooperation
by using Knowledge Algebra and Learn-Err methodology
supported by 3D-Conzilla