This page is a sub-page of our page on Entropy.
///////
Related pages:
///////
Historic entropy and the Bayesian approach to probability
Instead of “slicing time” into a sequence of separate moments, we can develop a model that respects the temporal order between moments in the sense that it connects any moment with its following (= next) moment in the sequence. In fact, we can define the corresponding entropy concept as a kind of “1-step backwards-shifted” type of Shannon entropy that could be termed historic entropy.
Definition: The historic entropy is given by the expression \, {\sum\limits_{i = 1}^{ n }} P_{i-1} {\log}_2 P_i .
Carrying out the same computation as for Shannon entropy, we get
2^{\, H_{istoric-entropy}} = 2^{\; \sum {P_{i-1} \log P_i}} = 2^{\; \sum {\log {P_i}^{P_{i-1}}}} = \prod {P_i}^{P_{i-1}} = \,
= ({P_1}^{P_0}) \, ({P_2}^{P_1}) \, ({P_3}^{P_2}) \, \cdots \, ({P_{now-1}}^{P_{now-2}}) ({P_{now}}^{P_{now-1}}) ({P_{now+1}}^{P_{now}}) \, .
Here \, P_0 \, could stand for “the initial moment” of history, which is referred to by cosmologists as “the big bang”, or it could stand for “the initial moment of the history of life”, i.e., the moment when self-replication and choices were introduced into the cosmic story.
In mathematics, the upper right corner above a symbol is often used to denote the domain of functions for which the symbol in question is regarded as the codomain. Accordingly, \, B^A \triangleq \{ \, f: A \rightarrow B \, \} \, denotes the set of all functions from \, A \, to \, B \, , i.e., the set of all functions \, f \, with domain \, A \, and codomain \, B \, .
Hence we see that each factor in the above product can be interpreted as the set of mappings from the corresponding previous moment into the corresponding next moment.
If we define \, {(P_{i-1})}_{P_i} \triangleq {P_{i}}^{P_{i-1}} , this product can be more ‘illuminatingly’ written as
\, {(P_{0})}_{P_1} \, {(P_{1})}_{P_2} \, {(P_{2})}_{P_3} \, \cdots \, {(P_{now-2})}_{P_{now-1}} \, {(P_{now-1})}_{P_{now}} \, {(P_{now})}_{P_{now+1}} \,with the same interpretation as before.
Temporal residue calculus:
{\int\limits_{n \in \mathbb{Z}}^{ \text {} }} N_{ow}^n = \int N_{ow}^{-1} = \log N_{ow} \, .
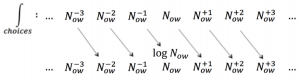
Figure 224: Choices made at the last moment integrate into the logarithm of the present moment.
///// Compare with Grothendieck’s category of elements construction
N_{ow} \equiv 2^{\; \log N_{ow}} = 2^{\; \; \int\limits_{c_{hoices}^{ \text {} }} N_{ow}^{-1}} .
N_{ow} \equiv 2^{\; \log N_{ow}} = 2^{\; \int N_{ow}^{-1}} = 2^{\; \int 2^{\; \int N_{ow}^{-2}}} = 2^{\; \int 2^{\; \int 2^{\; \int N_{ow}^{-3}}}} = \cdots \, .
The recursively logarithmic relationship between the Now and its Past:
The \, N_{ow} \, raised to the power of its \, P_{ast} \, is equal to
the \, N_{ow} \, raised to the power of (its \, L_{ast} \, raised to the power of its \, P_{ast} ) .
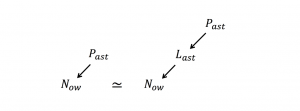
Figure 225: The Now raised to the power of the Past.
Focusing on the past, we have the situation depicted in Figure 225, i.e.,
\, {N_{ow}}^{P_{ast}} \simeq {N_{ow}}^{({L_{ast}}^{P_{ast}})} .
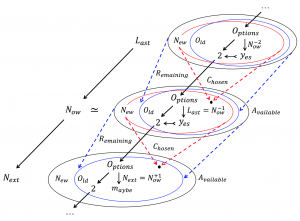
The choices are made from the options available at the last moment:
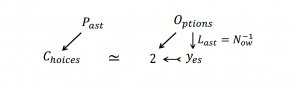
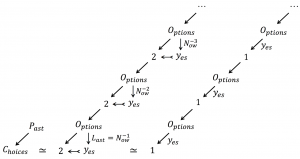
Figure 226: The choices of the past are closed (= already made)
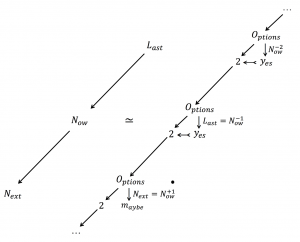
Figure 227: The choices of the future are still open (= not made yet)
Options Choice chain complex:
///////