This page is a sub-page of the page on our Mathematical Explainatorium.
///////
Related KMR pages
• Matteplåster (in Swedish)
• New Paradigms and Tools for Math Education
• Math Rehab
• What is Mathematics?
• Mathematics is Representation
• Learning Object Repository
///////
Other relevant sources of information:
///////
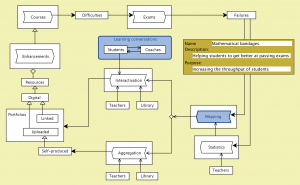
The purpose of the math bandages project is to stop the “bleeding” that stems from students not passing their math exams. One of the reasons for this is that students often have backward competence gaps with respect to mathematics, i.e., differences between what they know and what they should have known.
The math bandages project will try to diagnose such backward competence gaps and address them by pointing to adequate learning resources – both online and offline.
///////
Goal: Increased student throughput
Method: Difficulty mapping and didactic bottleneck interventions:
Helping the individual student to:
1. Identify what s/he needs to learn in order to solve exam problems of the type that s/he has failed to solve earlier – by applying knowledge gap mapping“, and suggest personalized interactive and targeted learning activities.
2. Identify what is experienced as difficult/impossible during an ongoing course or after a finished but not passed course and suggest actions that will help the student to pass the course exam next time.
A: Mapping:
• What material is lacking since earlier? There are diagnostic tests that can indicate backward knowledge gaps.
• Which parts of the course are most difficult to grasp, i.e., which parts have most failures on the exams?
• How do we teach these difficult parts?
• What material is used?
• How are the concepts related to each other in different courses?
B: Didactic bottleneck interventions:
1. Improvement of the problematic material by linking to alternative explanations in different online learning environments such as YouTube.
2. Knowledge aggregation by e.g., recording, post-processing and uploading appropriate learning objects, is fundamentally important in order to improve the learning outcome from the course material.
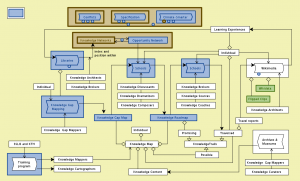
3. Interactivation of problematic concepts and figures: A well-known problematic moment in the study of mathematics is the traditional (and often very “reader-unfriendly”) relation between a figure (= a graphic illustration) and the describing text in a typical course book. The explaining figure, which often illustrates some form of dynamic relationship or process, is not only fixed and static but is often located on a different page in relation to the describing text. This leads to a repeated leafing back and forth when the reader tries to follow the reasoning of the text around what is going on in the corresponding figure.
By making use of so-called augmented reality the figures can be connected to interactive programs that can “breath life” into the formulas and enable the closing of experience-based cognitive feedback loops with great learning potential and power of insight. In this way the course provider can offer a personalizable interactivation service of problematic figures – as well as of other problematic parts of the course literature.
Outcome: Enhancing the cognitive feedback loop of the problematic material of the course by interactivation and knowledge aggregation.
///////
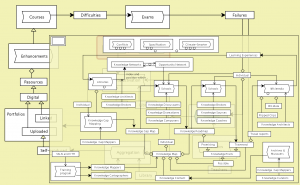
Math bandages model in Conzilla:
///////
Process model of a real math course:
Calculus for Bio and Chemistry at KTH Royal Institute of Technology, 2007:
[Gunnar Johnsson and Ambjörn Naeve in the Matriks project]
///////
• Algebra
///////
• Some basic algebraic concepts
Expected challenges to understanding:
• Relations
• Group, Ring, Field, Module, Vector Space
• Rings of Polynomials
• Disambiguating plus
///////
Expected challenges to understanding:
• Linear Transformations
• Vectors and their Coordinates in different Bases
• Eigenvalues and Eigenvectors
• Diagonalization of Quadrics
///////
• Calculus
///////
• Calculus of One Real Variable
Expected challenges to understanding:
• Taylor Expansion
• The Chain Rule
• Integration
• Fourier Series
///////
• Calculus of Several Real Variables
Expected challenges to understanding:
• Gradients
• Taylor Expansion
• The Chain Rule
• Different Coordinate Systems
///////
• Calculus of One Complex Variable
Expected challenges to understanding:
• Conformal Mapping
• Inversion
• Möbius Transformations
• Steiner Circles (and the Circle of Appollonius)
• Stereographic Projection
///////
• Geometry
• Metric Geometry
• Euclidean Geometry
• Geometric Shapes
///////
Expected challenges to understanding:
• Conics
• Evolutes and Involutes
///////
• Surfaces
Expected challenges to understanding:
///////
///////
Why Flipped Classes Often Flop
Folks:
The posting below gives some important suggestions on how to make flipped classrooms more effective. It is by Chandralekha Singh* and it appeared in the January 20, 2021 issue of Inside Higher Ed, an excellent – and free – online source for news, opinion, and jobs for all of higher education. You can subscribe by going to: http://insidehighered.com/. Also, for a free daily update from Inside Higher Ed, e-mail
Regards,
Rick Reis
reis@stanford.edu
Tomorrow’s Teaching and Learning
Why Flipped Classes Often Flop
(by Chandralekha Singh, Inside Higher Ed, January 20, 2021, http://insidehighered.com/ )
///////
TAKE HOME MESSAGE: We urge faculty members to keep a synchronous component in their courses as in the flipped courses and incentivize students with many low-stakes grade incentives interspersed throughout the course.
///////
The development of the internet and video-streaming services has prompted many educators to reimagine instruction. Salman Khan began Khan Academy by teaching his cousin and then making videos, which people have watched hundreds of millions of times. At the same time, researchers have recognized that “teaching by telling” is ineffective, and new models of instruction have emerged that promote more active engagement among students.
The flipped class/course model is one prominent example that colleges are widely implementing. This approach requires an instructor to interact with students but to behave more as a coach to help with problem solving or another concrete skill development, rather than being a sage on the stage during class time.
A different approach that takes advantage of internet/video resources is massive open online courses, in which most of the course content is asynchronous and anyone in the world can enroll for free and work through the materials at their own place. Popularized more than a decade ago, many observers touted MOOCs as harbingers of the end of institutions of higher education. MOOCs would require a few “star” instructors worldwide, and each institution would no longer need classrooms or “duplicate” professors. But so far, we have not seen those dire predictions for higher education come to pass. Only a small percentage of the people enrolled in MOOCs actually complete their courses, and they are generally students who already possess a college degree and are highly self-motivated.
The worldwide COVID-19 pandemic was highly disruptive to higher education, forcing institutions, instructors and administrators to make rapid choices about how to continue to educate students while remaining physically separated. This unusual situation enabled a natural experiment to take place in which many faculty members implemented a flipped course structure but varied other factors, such as how they evaluated students’ work.
Toward the end of fall 2020, we conducted individual hourlong interviews with 37 students who were science majors at the University of Pittsburgh about their experiences with remote instruction. We asked them to elaborate upon what they felt worked or did not work in their remote science classes. Our interviews suggest that policies related to grading of the out-of-class and in-class work was the most important determinant of whether many students kept up each week with both the out-of-class and in-class components of the flipped course as expected and whether they found their flipped classes effective. The findings are so clear and striking that the academic community should be aware of them as we prepare to continue instruction in the spring 2021 term.
We found overwhelmingly that when students had no grade incentive for doing out-of-class or in-class activities in a flipped course, and if solutions were posted on the course website after each class, many students simply stopped doing the weekly activities early on in the term. They only watched the relevant videos and browsed through all assessments right before each exam. They admitted that lack of grade incentive led them to deprioritize the weekly course activities.
A negative feedback loop occurred: students quickly realized that going to the class was “useless” if they had not done the out-of-class work involving watching videos and engaging with the corresponding assessments because the instructor immediately put them in a Zoom breakout roomand expected them to discuss their answers with their peers in small groups. A handful of students who had done the out-of-class work dominated the discussion while the unprepared majority was disengaged. Since prior engagement with video lectures was expected, the general discussions after each peer discussion in the Zoom breakout rooms were not productive for them, either.
In essence, flipped courses without a grade incentive to read the materials devolved into a course akin to asynchronous MOOCs but with a few high-stakes exams for most students. Many students did not keep up with the course and crammed a few days before each exam, something that has been shown to be detrimental for long-term retention. By contrast, most students found flipped courses in a remote format that were otherwise similar yet had a grade incentive were effective, and they kept up with those courses.
Interviewed students also noted that some instructors had made their course completely asynchronous with video lectures and had turned their allocated class time into office hours. All that counted toward a grade in their course were a few exams. Many students confessed that they did not go to the office hours because they did not keep up with the video lectures and crammed the material right before the exams. In general, these students were very dissatisfied with their learning in the asynchronous course. The dissatisfaction did not stem from lack of effort on the part of the instructors, who in good faith spent a tremendous amount of time and effort to make customized flipped videos for their course. Rather, it resulted from the structure of the course, which was not conducive to effective instruction.
Thus, the unplanned remote instruction this past term, in which instructors had different grading policies for flipped courses but otherwise had similar course structure, confirms that many students have difficulty with self-regulation and keeping up with course materials without a grade incentive each week. This lack of incentives to encourage students to effectively manage their time and be self-disciplined throughout is a major reason why the current MOOC framework has not succeeded in replacing traditional instruction.
What are the lessons going forward for remote instruction next term based upon these findings?
We urge faculty members to keep a synchronous component in their courses as in the flipped courses and incentivize students with many low-stakes grade incentives interspersed throughout the course. Such incentives are vital for ensuring that instructors’ efforts in remote instruction bear fruit and students learn and benefit from engaging with course materials throughout the term. At the same time, we also encourage instructors to be flexible and accommodate a handful of students who cannot keep up with the course material each week due to the adversity caused by the pandemic. They should find ways to assess those students’ performance using flexible approaches that differ from those they use for the rest of the class.
Bio Chandralekha Singh is a professor in the department of physics and astronomy and director of the discipline-based Science Education Research Center at the University of Pittsburgh and serves as president of the American Association of Physics Teachers.
Read more by Chandralekha Singh
“Desktop faculty development 100 times per year.”
At over 1,000 institutions in more than 100 countries
TOMORROW’S PROFESSOR eMAIL NEWSLETTER
Archives of all past postings can be found here:
Sponsored by the Center for Teaching and Learning at Stanford University.
///////
A conversation at KTH between David Hestenes and Ambjörn Naeve (August 2014):
///////
Hestenes on Conceptual Learning 1:

Hestenes on Conceptual Learning 2:
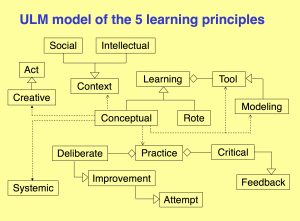
Hestenes on Conceptual Learning 3:

Hestenes on Conceptual Learning 4:

Hestenes on Conceptual Learning 5:

Hestenes on Conceptual Learning 6:
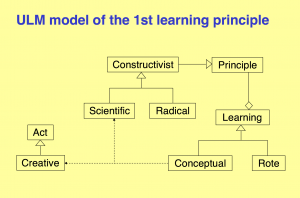
Hestenes on Conceptual Learning 7:

Hestenes on Conceptual Learning 8:

Hestenes on Conceptual Learning 9:

Hestenes on Conceptual Learning 10:

///////