This page is a sub-page of our page on Entropy.
///////
The sub-pages of this page are:
///////
Other relevant sources of information:
• Von Neumann Entropy (at Wikipedia)
///////
Named “information entropy” by its inventor Claude Shannon.
/////// Shannon, 1948: A Mathematical Theory of Communication
/////// According to Ian Stewart (2013, p. 274):
Shannon [then] provided a solid foundation for his definition by listing several basic principles that any measure of information content ought to obey and deriving a unique formula that satisfied them. His set-up was very general: the message could choose from a number of different symbols, occurring with probabilities \, P_1, P_2, … \, , P_n \, where \, n \, is the number of symbols. The information \, H \, conveyed by a choice of one of these symbols should satisfy:
1) \, H \, is a continuous function of \, P_1, P_2, … \, , P_n . That is, small changes in the probabilities should lead to small changes in the amount of information.
2) If all probabilities are equal, which implies that they are all \, \frac {1}{n} \, , then \, H \, should increase if \, n \, gets larger. That is, if you are choosing between 3 symbols, all equally likely, then the information you receive should be more than if the choice were between just 2 equally likely symbols; a choice between 4 symbols should convey more information than a choice between 3 symbols, and so on.
3) If there is a natural way to break a choice down into two successive choices, then the original function \, H \, should be a simple combination of the new \, H -functions.
[…]
Shannon proved that the only function \, H \, that obeys his three principles is:
\, H = -P_1 {\log}_2 P_1 - P_2 {\log}_2 P_2 - \cdots - P_n {\log}_2 P_n = - {\sum\limits_{i = 1}^{ n }} P_i {\log}_2 P_i \,or a constant multiple of this expression, which basically just changes the unit of information, like changing from feet to meters.
/////// End of quote from (Stewart, 2013)
Shannon entropy and the frequentist approach to probability:
The Shannon entropy of information is defined by the formula \, H = - {\sum\limits_{i = 1}^{ n }} P_i {\log}_2 P_i \, .
As described above, it defines how much information a message contains, in terms of the probabilities with which symbols that make it up are likely to occur.
It is instructive to see what happens if one carries out the following computation:
2^{\, S_{hannon-entropy}} = 2^{\; \sum {P_i \log P_i}} = 2^{\; \sum {\log {P_i}^{P_i}}} = \prod {P_i}^{P_i} \, .
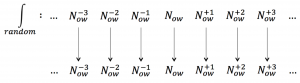
Figure 223: Randomness implies the separateness of moments
We see from Figure 223 that randomness implies the separateness of moments. Each moment appears “in isolation” and there are no connections between them. This is why Shannon entropy is insensitive to Time. This fact is central to the frequentist (= stochastic-variables-based) approach to probability, since this approach hinges on the (idealized) concept of “repeatability” (= repeatable experiments).
///////