This page is a sub-page of our page on Mathematical Concepts
///////
Related KMR-pages:
• Homotopy
• Oscar Reutersvärd
• M.C. Escher
• Disambiguation
• Entropy
• Function
• Homology and Cohomology
• Homotopy
• Space
• Time
• Products
• Topos
• Duality
• Topology
• Uncertainty
• Dimension
///////
Other relevant sources of information:
• …
///////
From “do not divide by zero” to “divide out by that which you want to turn into zero”
You can’t make something from nothing.
— Aristotle
But you can make nothings from somethings
by dividing out with the latter
and in the world of rings
these somethings are called ideals.
— Emmy Noether
///////
“Dividing out” from a mathematical space:
creating a quotient space by disregarding a subspace:
• Ring / Ideal = Quotient ring
• Group / Normal subgroup = Quotient group
• Vector space / Linear subspace = Quotient space
• Module / Submodule = Quotient module
///////
The kinds of igno-spaces that we have
give the kinds of zeros that we can create.
The zero-creating process is called “dividing out by”
\, S_{pace} \, \equiv \, U_{niverse} \, / \, i_{gno}S_{pace} \, \, T_{ime} \, \equiv \, U_{niverse} \, / \, i_{gno}T_{ime} \,with \; i_{gno}\, i_{gno} \, \equiv \, 1 .
///////
\, S_{pace} \, \otimes \, T_{ime} \, \equiv \, \, \equiv \, R_{evertable}T_{hings} \, \otimes \, i_{rr}R_{evertable}T_{hings} \, \equiv \, \, \equiv \, I_{invertable}T_{hings} \, \otimes \, n_{on}I_{invertable}T_{hings} \, \,with \; i_{rr}\, i_{rr} \, \equiv \, n_{on} \, n_{on} \, \equiv 1 .
///////
Weekday calendar:
\, {\mathbb{Z}}_7 \, \stackrel {\mathrm{def}}{=} \, \mathbb{Z} \, / \, 7\mathbb{Z} \,///////
The concept of equivalence:
Two structures are equivalent if and only if
there exists an invertible and structure-preserving map
(a so-called isomorphism) between them.
— Nicholas Bourbaki
///////
The power of thinking is knowing what not to think about:
\, {T_{hinking}}^{P_{ower}} \, = \, \{ \, f \, : \, P_{ower} \, \xrightarrow[ \; no \; ]{ \; yes \; } \, T_{hinking} \, \} \, = \, \, = \, \{ \, f \, : \, P_{ower} \, \xrightarrow[ \; disregard \; ]{ \; focus \ on \; } \, T_{hinking}\, \} \, [ \, {T_{hinking}}^{\bold{2}} \, ]_{R_{elations}} \, \mapsto \, \left< \, B_{inary} \, T_{hinking} \, \right>_{R_{elations}} \, \mapsto \, \left< \, m_{ultigraph} \, \right>_{R_{elations}} \,///////
\, [ \, {T_{hinking}}^{\bold{3}} \, ]_{R_{elations}} \, \mapsto \, \left< \, T_{ernary} \, T_{hinking} \, \right>_{R_{elations}} \, \mapsto \, \left< \, h_{ypergraph} \, \right>_{R_{elations}} \, \, [ \, {T_{hinking}}^{\bold{\Omega}} \, ]_{R_{elations}} \, \mapsto \, \left< \, E_{volutionary} \, T_{hinking} \, \right>_{R_{elations}} \,• Topos
• Subobject classifier
• Historic entropy
• Evolutionary entropy
///////
Evolutionary entropy 1:
Options-generating function:
Evolutionary entropy 2:
Evolutionary entropy 3:
By including the \, N_{ext} \, term which corresponds to \, i = 1 \,
we have
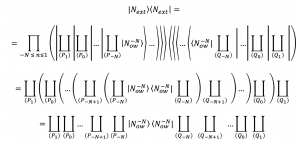
///////
Quoting Naeve, A., The Garden of Knowledge as a Knowledge Manifold (1997, p. 94):
12. Establishing equality by disregarding differences
12.1 Disregarding the Subjective Observer (= Oneself)
In his brilliant lectures, Schrödinger asks the fundamentally important question: What are the peculiar, special traits of our scientific world-picture? About one of these fundamental features, (he goes on to state) there can be no doubt: It is the hypothesis that the Display of Nature can be understood [Nature and the Greeks, [(146), p. 90]. It is the non-spiritistic, the non-superstitious, the non-magical outlook. A few pages later, Schrödinger continues [Loc. Cit, p. 92]:
There is, however, so I believe, a second feature, much less clearly and openly displayed, but of equally fundamental importance. It is this, that science in its attempt to describe and understand Nature simplifies this very difficult problem. The scientist subconsciously, almost inadvertently, simplifies his problem of understanding Nature by disregarding or cutting out of the picture to be constructed, himself, his own personality, the subject of cognizance.
Inadvertently the thinker steps back into the role of an external observer. This facilitates the task very much. But it leaves gaps, enormous lacunae, leads to paraxoxes and antinomies whenever, unaware of this initial renunciation, one tries to find oneself in the picture or to put oneself, one’s own thinking and sensing mind, back into the picture.
This momentous step, cutting out oneself, stepping back into the position of an observer who has nothing to do with the whole performance – has received other names, making it appear quite harmless, natural, inevitable. It might be called just objectivation, looking upon the world as an object. The moment you do that, you have virtually ruled yourself out. A frequently used expression is ‘the hypothesis of a real world around us’ (Hypothese der realen Aussenwelt). Why, only a fool would forgo it! Quite right, only a fool. None the less it is a definite trait, a definite feature of our way of understanding Nature – and it has consequences.
The clearest vestiges of this idea that I could find in ancient Greek writing are those fragments of Heraclitus that we have been discussing and analyzing just before. For it is this ‘world in common’ this ξυνον or κοινον of Heraclitus, that we are constructing; we are hypostatizing the world as an object, making the assumption of a real world around us – as the most popular phrase runs – made up of overlapping parts of our several consciousnesses. And in doing so, everyone willy-nilly takes himself – the subject of cognizance, the thing that says ‘cogito ergo sum’ – out of the world, removes himself from it into the position of an external observer, who does not himself belong to the party. The ‘sum’ becomes ‘est’.
Is that really so, must it be so, and why is it so? For we are not aware of it.
I’ll say presently why we are not aware of it. First let me say why it is so.
Well, the ‘real world around us’ and ‘we ourselves’, i.e. our minds, are made up of the same building material, the two consist of the same bricks, as it were, only arranged in a different order – sense perceptions, memory images, imagination, thought. It needs, of course, some reflection, but one easily falls in with the fact that matter is composed of these elements and nothing else. Moreover, imagination and thought take an increasingly important part (as against crude sense-perception), as science, knowledge of nature, progresses.
///// Compare \, T_{hinking}S_{pace} \, \equiv \, H_{om}( \, U_{niverse}, M_{ind} \, ) \,
What happens is this. We can think of these – let me call them elements – either as constituting mind, every- one’s own mind, or as constituting the material world. But we cannot, or can only with great difficulty, think both things at the same time. To get from the mind-aspect to the matter-aspect or vice versa, we have, as it were, to take the elements asunder and to put them together again in an entirely different order. For example – it is not easy to give examples, but I’ll try – my mind at this moment is constituted by all I sense around me: my own body, you all sitting in front of me and very kindly listening to me, the aide-mémoire in front of me,
and, above all, the ideas I wish to explain to you, the suitable framing of them into words. But now envisage any one of the material objects around us, for example my arm and hand. As a material object it is composed, not only of my own direct sensations of it, but also of the imagined sensations I would have in turning it round, moving it, looking at it from different angles; in addition it is composed of the perceptions I imagine you to have of it, and also, if you think of it purely scientifically, of all you could verify and would actually find, if you took it and dissected it, to convince yourself of its intrinsic nature and composition. And so on. There is no end to enumerating all the potential percepts and sensations on my and on your side that are included in my speaking of this arm as of an objective feature of the ‘real world around us’.
The following simile is not very good, but it is the best I can think of: a child is given an elaborate box of bricks of various sizes and shapes and colours. It can build from them a house, or a tower, or a church, or the Chines wall, etc. But it cannot build two of them at the same time, because it is, at least partly, the same bricks it needs in every case.
This is the reason why I believe it to be true that I actually do cut out my mind when I construct the real world around me. And I am not aware of this cutting out. And then I am very astonished that the scientific picture of the real world around me is very deficient. It gives a lot of factual information, puts all our experience in a magnificently consistent order, but it is ghastly silent about all and sundry that is really near to our heart, that really matters to us. It cannot tell us a word about red and blue, bitter and sweet, physical pain and physical delight; it knows nothing of beautiful and ugly, good or bad, God and eternity. Science sometimes pretends to answer questions in these domains, but the answers are very often so silly that we are not inclined to take them seriously.
So, in brief, we do not belong to this material world that science constructs for us. We are not in it, we are outside. We are only spectators. The reason why we believe that we are in it, that we belong to the picture, is that our bodies are in the picture. Our bodies belong to it. Not only my own body, but those of my friends, also of my dog and cat and horse, and of all the other people and animals. And this is my only means of communicating with them.
Moreover, my body is implied in quite a few of the more interesting changes – movements, etc. – that go on in this material world, and is implied in such a way that I feel myself partly the author of these goings on. But then comes the impasse, this very embarrassing discovery of science, that I am not needed as an author. Within the scientific world-picture all these happenings take care of themselves, they are amply accounted for by direct energetic interplay. Even the human body’s movements ‘are its own’ as Sherrington put it. The scientific world-picture vouchsafes a very complete understanding of all that happens – it makes it just a little too understandable. It allows you to imagine the total display as that of a mechanical clockwork, which for all that science knows could go on just the same as it does, without there being consciousness, will, endeavor, pain and delight and responsibility connected with it – though they actually are.
And the reason for this disconserting situation is just this, that, for the purpose of constructing the picture of the external world, we have used the greatly simplifying device of cutting our own personality out, removing it; hence it is gone, it has evaporated, it is ostensibly not needed. In particular, and most importantly, this is the reason why the scientific world-view contains of itself no ethical values, no aesthetic values, not a word about our own ultimate scope or destination, and no God, if you please. Whence came I, whither go I?
Science cannot tell us a word about why music delights us, of why and how an old song can move us to tears. Science, we believe, can, in principle, describe in full detail all that happens in the latter case in our sensorium and ‘motorium’ from the moment the waves of compression and dilation reach our ear to the moment when certain glands secrete a salty fluid that emerges from our eyes. But of the feelings of delight and sorrow that accompany the process science is completely ignorant – and therefore reticient.
Science is reticient too, when it is a question of the great Unity – the One of Parmenides – of which we all somehow form part, to which we belong. The most popular name for it in our time is God – with a capital ‘G’. Science is, very usually, branded as being atheistic. After what was said, this is not astonishing. If its world-picture does not even contain blue, yellow, bitter, sweet – beauty, delight and sorrow – , if personality is cut out of it by agreement, how should it contain the most sublime idea that presents itself to the human mind?
/////// End of Quote from Schrödinger.
12.2 Equality as Relative Indifference
Equality is considered to be context-based, i.e. circumstantial. Equality is always investigated (taken to hold) relative to some presupposed context which is more or less unspeakable and therefore has to be tacitly agreed upon. For instance, when we state that ‘X is equal to Y’, we obviously disregard the difference in shape of the two letters. In fact, equality always requires someone, i.e. an externally observing subject, in order to compare the two candidates. Hence:
Fact 17: Equality is always taken relative to an observer (= someone). Two things are equal (equivalent) when (and only when) the observer is unaware of – or chooses to disregard –
their difference [1].
In this way, each kind of equality is equipped with its own protocol-of-disregards, a kind of protocol that defines ‘in what sense’ the corresponding items are ‘equal’ to one another. We could say that we describe the equality in terms of its disregarded concerns. This forces us to attempt to formulate these concerns, which places the given type of equality within a more general context and high-lights the equivalence-classes that are involved in its application.
This is the essence of abstract thinking – being sensitive to what differences and aspects of a problem that can be disregarded without losing touch of its essential structure.[2] Relevance is obtained by systematically disregarding irrelevance, which can be expressed in the following
Fact 18: The power of thinking is knowing what not to think about.
Definition 24: The disregarded concerns of an equality are are called its indifference-
space.
The observing subject was (implicitly) introduced into mathematics by Kurt Gödel in his famous paper of 1931 [(64)]. There he proves the unavoidable existence of certain logical statements within any formal theory that embraces the infinity of natural numbers (in a recursively defined way). These statements are basically just formal encodings of the phrase ‘this statement cannot be proved’, which implies that they are not logically decidable, i.e. ‘verifiable’ or ‘falsifiable’ within the formal system. However, they are by their very nature ‘true’, but this truth is a form of ‘meta-truth’, which necessarily requires an externally observing subject in order to be recognized.
From a philosophical point of view, we can summarize these achievements in:
Fact 19: In [(64)] Gödel establishes the logical necessity of subjectifying mathematics once and for all. He ‘writes the observer into the equations’, so to say, without
any logical possibility of ever ruling her out. [3]
13 A Formal Model of Participator Consciousness
We make use of our Perception/Conception Duality (yin/yang pair) of Induction/Deduction in order to build coherent patterns (representations) of the world and our own relations to it.
What came first, the experiment or the conceptual framework? This is a ‘chicken-and-egg’ type of situation where each one needs the other in order to develop properly. Hence they display a duality which is similar to the yin and yang symbol of ancient Chinese philosophy.
13.1 Making Sense is Disregarding Nonsense
Whenever it comes knocking on your windows, experience presents itself as a set of readings on your sense-monitors. Two different knocks will trigger the same reading it the monitor is unaware of their difference. The process of sensing is equivalent to ignoring nonsense.
Definition 25: A perceptor is an organ that is aware of the universe
Definition 26: Awareness, i.e., being aware, is a mapping from the universe to the perceptor.
Definition 27: Im(Awareness) = Sense(Perceptor) is the space of perceptor-awareness.
Definition 28: Ker(Awareness) = Nonsense(Perceptor) is the space of perceptor-ignorance
Fact 20: Sense = Universe/Nonsense.
According to Fact 20, The sensual image is always perceived modulo its corresponding kernel of perceptor-awareness. Hence, a perceptor makes sense from the universe by disregarding its own non-sense.
• It is the nature of perception to experience (= conceptualize) reality as a direct sum of sense and nonsense.
• It is the aim of perception to reconstruct – from its memory of the universe as it was, modulated by the sensual image as it is – a unique experience which is coherent with the others.
• It is the purpose of perception to reconcile the inductive evidence of the image with the deductive predictions of the conceptual model.
• It is by the structure of perception that this reconstruction is performed by a suitable choice of non-sense, guided by deductive assumptions in the model. (“We assume that …, hence we can conclude that …”)
//// INJECT FIG 39 HERE
Fig. 39. The short exact sequence of a disregarded aspect.
Fig. 40. The chain complex of disregarded aspects.
Each change, the effects of which are neglected by its iterates (change2 = 0) creates a chain complex. Each aspect of it creates a subcomplex. The disregard of this aspect creates the corresponding quotient complex.
13.2 The Participator as a System of Perceptors
Definition 30: A system S is a family of objects and arrows – with at most one arrrow between each pair – which is closed under concatenation, i.e. the concatenation of two subsequent arrows of S is always an arrow of S.
A system determines a coherence condition between its different parts. It is clear that if one follows two different paths between to given objects in a system, the resulting arrow will always be the same (since the diagram is commutative). We say that a system is internally coherent, or that it is coherent with itself.
Definition 31: A participator is a system of perceptors, linked together in some form of biological unity.
Each specific implementation of such biological unity (= type of species) implies its own specific coherence condition on the performance of the individual perceptors in relation to each other. Such a condition can be thought of as a form of ‘common protocol’ for mutual interaction.
In fact let us generalize the concept of coherence, by making the following
Definition 32: Two systems are said to be mutually coherent (= satisfy a coherence relation) when they conform to a common protocol.
13.3 The Actor/Reactor Consciousness
Consider the participator \, P \, given by the system of perceptors \, \{ \, P_i : i \in I \, \} \, .
We will denote this relationship by \, P \, \equiv \, \oplus P_i .
Definition 33: The actor- and reactor consciousness, \, P_{A{ct}} \, respectively \, P^{R_{eact}} \,
of the participator \, P \, \equiv \, \oplus P_i , are defined by:
PAct = limPi , PReact = limPi →← (7)
In the role of actor, the coherence protocol is implemented by ‘obedience’ (we act coherently == we obey), and in the role of reactor the coherence protocol is implemented by ‘agreement’ (we react coherently == we agree). Hence the concepts of obedience and agreement form a kind of dynamic duality that reflects the corresponding structure of the ‘coherence-protocol’ of the actor/reactor duality of behaviour. Expanding the semantics, we can write
ParticipatorAct = colim Perceptor_i , Participator React = lim Perceptor_i →←
The <target|observer> notation is introduced in [(116)]. Since a participator has both a <target| and=”” an=”” |observer=””> aspect, we can introduce the natural representation</target|></target|observer>
Participator = Target ⊕ Observer (8)
perceive
conceive
Fig. 41. The Yin-Yang type of interaction duality between perceive and conceive.
This makes the target-observer aspects correspond precisely to the natural projections:
〈Participator| = 〈Target ⊕ Observer| = 〈Target| |Participator〉 = |Target ⊕ Observer〉 = |Observer〉
From (3) and (4) we can deduce four natural types of participator behaviour:
(9)
(10)
Action
Reaction
TargetReact ⊕ObserverAct , React
TargetAct ⊕ObserverReact React
Target Act ⊕ Observer ,
Theses behaviours are represented by the four different rounded squares of Figure 42.
Definition 34:
//// FIG 42 GOES HERE
Fig. 42. The Act-React as a Target-Observer patterns.
Given a participator \, P , a change is a couple U -> U ->P -> U (before, after). Two changes are coherent, if there are morphisms \, P \, \rightarrow \, P \, \rightarrow P \, such that the diagram commutes.
For each individual participator \, P \, this defines a class of coherent changes in a natural way. Moreover, in the spirit of Poincaré [1] I make the following:
Definition 35: Space is the class of invertible coherent changes (= the undoable).
Definition 36: Time is the class of non-invertible coherent changes (= the non-undoable).
The concepts of a participator are the structures that remain invariant under a large enough sub-group of its actions and its reactions. These are the nouns of its conceptor geometry. The verbs of the conceptor geometry are the changes that are perceptible and coherent to the participator. Each participator has an anticipator and a verificator.
Definition 37: The participator is said to be relaxed when its verification is exact.
In this case we have the exact triangle: Before->After->Participator depicted in Figure 43.
///// Exact Triangle goes Here
Fig. 43. The exact triangle pattern of anticipation and verification.
Fact 21: Science contains a non-exact couple of deductive anticipation and inductive verification. The so called “scientific process” is driven by the lack of exactness for
this couple, which goes by the name of astonishment [1] and which is inextricably linked to curiosity.
[1]: According to Schrödinger [(146), p. 57]: “The first requirement of a scientist is to be curious. He must be capable of being astonished and eager to find out. Plato, Aristotle and Epicurus emphasize the import of being astonished (θαυμαζειν). And this is not trivial when it refers to general questions about the world as a whole; for, it is given us only once, we have no other one to compare it with.”
13.4 Building a Knowledge Manifold by Calibrating Knowledge Patches
A Kowledge Manifold represents a kind of network that carries within itself the ‘informational coherence’ of a culture. Any implementation of a Knowledge Manifold is constructed – just as a standard mathematical manifold [2] – by the successive calibration of local patches (= overlap- ping coordinate transformations).
[2]: A manifold is a mathematical concept that provides a suitable metaphor for a general (= abstract) description of the knowledge-formation-process. In modern mathematics, a manifold is just an atlas of patch coordinate systems that overlap smoothly with each other. If the atlas is maximal, it is called a differentiable structure, and we speak about a differentiable manifold. This concept plays a fundamental role in the mathematical description system of theoretical physics.
An important part of a Knowledge Manifold (KM) is given by its calibration protocols. This is a set of rules which are either obeyed (in the active mode) or agreed upon (in the reactive mode) – depending on how you choose to interact with the surrounding patches.
By defining an idea (= concept) as a representation of an experience, (Definition 21, a Knowledge Manifold starts from a collection of subjective views (individual Knowledge Patches) that are linked together – by calibration of individual views – into the ‘objective world’, i.e. the ‘real world’ around us.
This way of conceptual modeling focuses on the individual – as opposed to the collective – way of relating to knowledge. It is designed as a framework to support subjective education, i.e. individually based learning strategies that are developed in a cooperative process between the learners and the teachers.
/////// End of Quote from (Naeve, 1997).

