This is a sub-page of our page on Calculus of One Real Variable.
Related KMR pages:
• Differentiation and Affine Approximation (in One Real Variable).
• Differentiation and Affine Approximation (in Several Real Variables).
• The Chain Rule (in several real variables)
///////
Anchors into the text below:
• The chain rule expressed through a combination of affine approximations
• Forward and backward combinations of affine approximations
• Basic diagram for an affine approximation
• Forward expansion of the basic diagram
• Backward expansion of the basic diagram
• Affine approximation in one dimension
• Adapted to pullback of x = x(u)
• The chain rule for functions from R1 to R1 to R1
• The basic diagram for an affine approximation in 1D
• Expand the diagram to the right
• A movie of the chain rule for functions from R1 to R1 to R1
///////
The Chain Rule expressed through a combination of Affine Approximations
Let \, X, Y \, and \, Z \, be linear spaces and let \, g : Z \leftarrow Y \, and \, f : Y \leftarrow X \, be two differentiable functions. Select a point \, \textcolor{blue}{p} \in X \, as well as its successive image points \, f(\textcolor{blue}{p}) \in Y \, and \, g(f(\textcolor{blue}{p})) \in Z . We then have
\, Z_{g(f(\textcolor{blue}{p}))} \, \xleftarrow{\, g} \, Y_{f(\textcolor{blue}{p})} \, \xleftarrow{\, f} \, X_{\textcolor{blue}{p}} \,
where \, X_{\textcolor{blue}{p}} \, , \, Y_{f(\textcolor{blue}{p})} \, , \, Z_{g(f(\textcolor{blue}{p}))} \, are the maximal affine subspaces of \, X \, , Y \, , \, Z \,
that correspond to the chosen points \, \textcolor{blue}{p}, f(\textcolor{blue}{p}), and \, g(f(\textcolor{blue}{p})) .
We can think of these maximal subspaces as the affine spaces that arise when we chose a fixed point in the corresponding linear spaces. This choice brings with it a linear space of displacement vectors that act by displacement (or translation) on the vectors of the original linear space.
The corresponding affine approximations
\, Z_{g(f(\textcolor{blue}{p}))} \, \xleftarrow{\, g_{f(\textcolor{blue}{p})}} \, Y_{f(\textcolor{blue}{p})} \, \xleftarrow{\, f_{\textcolor{blue}{p}}} \, X_{\textcolor{blue}{p}} \, ,
where
\, Y_{f(\textcolor{blue}{p})} \ni f(\textcolor{blue}{p}) + {f'(x)}_{\textcolor{blue}{p}} \, \textcolor{red}{\Delta x} \, \xleftarrow{\,\,\, f_{\textcolor{blue}{p}} \,\,\,} \shortmid \, \textcolor{blue}{p} + \textcolor{red}{\Delta x} \in X_{\textcolor{blue}{p}} \,
and
\, Z_{g(f(\textcolor{blue}{p}))} \ni g(f(\textcolor{blue}{p})) + {g'(f)}_{f(\textcolor{blue}{p})} \, \textcolor{red}{\Delta f} \, \xleftarrow{\,\,\, g_{f(\textcolor{blue}{p})} \,\,\,} \shortmid \, f(\textcolor{blue}{p}) + \textcolor{red}{\Delta f} \in Y_{f(\textcolor{blue}{p})} \,
combine into
\, Z_{g(f(\textcolor{blue}{p}))} \ni (g \circ f)(\textcolor{blue}{p}) + {(g \circ f)'(x)}_{\textcolor{blue}{p}} \, \textcolor{red}{\Delta x} \, \xleftarrow{\,\,\, {(g \circ f)}_{\textcolor{blue}{p}} \,\,\,} \shortmid \, \textcolor{blue}{p} + \textcolor{red}{\Delta x} \in X_{\textcolor{blue}{p}}
and their linear parts combine into the matrix product
\, {(g \circ f)'(x)}_{\textcolor{blue}{p}} = {g'(f)}_{f(\textcolor{blue}{p})} \, {f'(x)}_{\textcolor{blue}{p}} .
The combination of the linear parts is called the chain rule and is, in a sense, the starting point of calculus. We will see how it unfolds and generalizes the number concept when we deal with functions of several real variables.
We can arrange the combined actions of these maps in the following diagrams presented below.
Notation: The vertical arrows mean membership in the corresponding linear spaces or affine subspaces at the top.
Forward and backward combinations of affine approximations
Basic diagram for an affine approximation:
\, \begin{matrix} Y & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\; f \;\;\;\;\;\;\;\;\;\;\;\;\;}} & X \\ \uparrow & & \uparrow \\ f(x) & {\xleftarrow{\, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & x \\ & & & \\ Y_{f(\textcolor{blue} {p})} & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\; f_{\textcolor{blue}{p}} \;\;\;\;\;\;\;\;\;\;\;}} & X_{\textcolor{blue}{p}} \\ \uparrow & & \uparrow \\ f(\textcolor{blue} {p}) + f'(x)_{\textcolor{blue} {p}} \, \textcolor{red} {\Delta x} & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & {\textcolor{blue}{p} + \textcolor{red} {\Delta x}} \end{matrix}
Note: The “forward” direction is represented “from the right to the left”. The reason for this is to be compatible with the matrix algebra that will emerge through the chain rule.
///////
Forward expansion of the basic diagram (= operating with the function \, g \, from the left):
\, \begin{matrix} Z & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\; g \;\;\;\;\;\;\;\;\;\;\;\;\;}} & Y & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\; f \;\;\;\;\;\;\;\;\;\;\;\;\;}} & X \\ \uparrow & & \uparrow & & \uparrow \\ g(f(x)) & {\xleftarrow{\, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & f(x) & {\xleftarrow{\, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & x \\ & & & & & & & \\ Z_{g(f(\textcolor{blue} {p}))} & {\xleftarrow{\;\;\;\;\;\;\;\;\; g_{f(\textcolor{blue} {p})} \;\;\;\;\;\;\;\;\;}} & Y_{f(\textcolor{blue} {p})} & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\; f_{\textcolor{blue}{p}} \;\;\;\;\;\;\;\;\;\;\;}} & X_{\textcolor{blue}{p}} \\ \uparrow & & \uparrow & & \uparrow \\ & & f(\textcolor{blue} {p}) + f'(x)_{\textcolor{blue} {p}} \, \textcolor{red} {\Delta x} & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & {\textcolor{blue}{p} + \textcolor{red} {\Delta x}} \\ g(f(\textcolor{blue} {p})) + g'(f)_{f(\textcolor{blue} {p})} \, \textcolor{red} {\Delta f} & { \xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & f(\textcolor{blue} {p}) + \textcolor{red} {\Delta f} & & \\ & & & & & & & \\ Z_{g(f(\textcolor{blue} {p}))} & & {\xleftarrow{\, { \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (g \circ f)}_{\textcolor{blue}{p}} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; } } & & X_{\textcolor{blue}{p}} \\ \uparrow & & & & \uparrow \\ (g \circ f)(\textcolor{blue} {p}) + {(g \circ f)'(x)}_{\textcolor{blue} {p}} \, \textcolor{red} {\Delta x} & & {\xleftarrow{\, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & & {\textcolor{blue}{p} + \textcolor{red} {\Delta x}} \end{matrix}
///////
Backward expansion of the basic diagram to the right by the substitution \, x = x(u) ,
which is a pullback of the variable \, x \, :
\, \begin{matrix} Y & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\; f \;\;\;\;\;\;\;\;\;\;\;\;\;}} & X & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\; x \;\;\;\;\;\;\;\;\;\;\;\;\;}} & U \\ \uparrow & & \uparrow & & \uparrow \\ f(x(u)) & {\xleftarrow{\, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & x(u) & {\xleftarrow{\, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & u \\ & & & & & & & \\ Y_{f(x(\textcolor{blue} {p}))} & {\xleftarrow{\;\;\;\;\;\;\;\;\; f_{x(\textcolor{blue} {p})} \;\;\;\;\;\;\;\;\;}} & X_{x(\textcolor{blue} {p})} & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\; x_{\textcolor{blue}{p}} \;\;\;\;\;\;\;\;\;\;\;}} & U_{\textcolor{blue}{p}} \\ \uparrow & & \uparrow & & \uparrow \\ & & x(\textcolor{blue} {p}) + x'(u)_{\textcolor{blue} {p}} \, \textcolor{red} {\Delta u} & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & {\textcolor{blue}{p} + \textcolor{red} {\Delta u}} \\ f(x(\textcolor{blue} {p})) + f'(x)_{x(\textcolor{blue} {p})} \, \textcolor{red} {\Delta x} & { \xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & x(\textcolor{blue} {p}) + \textcolor{red} {\Delta x} & & \\ & & & & & & & \\ Y_{f(x(\textcolor{blue} {p}))} & & {\xleftarrow{\, { \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (f \circ x)}_{\textcolor{blue}{p}} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; } } & & U_{\textcolor{blue}{p}} \\ \uparrow & & & & \uparrow \\ (f \circ x)(\textcolor{blue} {p}) + {(f \circ x)'(u)}_{\textcolor{blue} {p}} \, \textcolor{red} {\Delta u} & & {\xleftarrow{\, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid } & & {\textcolor{blue}{p} + \textcolor{red} {\Delta u}} \end{matrix}
///////
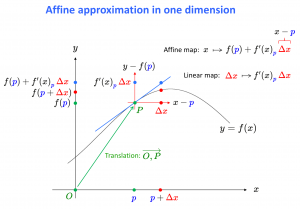
Affine approximation in one dimension
\, x_{\textcolor{blue} {p}} \,\, , f_{x(\textcolor{blue} {p})} \,\, , \,\, f \circ x \, , \, (f \circ x)_{\textcolor{blue} {p}} \,\, , \,\, f(\textcolor{blue} {p} + \textcolor{red} {\Delta x}) \, f(\textcolor{blue}{p}) - {f'(x)}_{\textcolor{blue}{p}} \, \textcolor{red} {\Delta x} .
///////
\, \begin{matrix} Y & {\xleftarrow{\;\;\;\;\;\;\;\;\; f \;\;\;\;\;\;\;\;\;}} & X \\ \uparrow & & \uparrow \\ f(x) & \xleftarrow{\qquad \qquad \qquad}\shortmid & x \\ & & & & \\ Y_{f(\textcolor{blue}{p})} & {\xleftarrow{\;\;\;\;\;\;\;\;\; f_{\textcolor{blue}{p}} \;\;\;\;\;\;\;\;\;}} & X_{\textcolor{blue}{p}} \\ \uparrow & & \uparrow \\ f(\textcolor{blue}{p}) + {f'(x)}_{\textcolor{blue}{p}} \, \textcolor{red} {\Delta x} & {\xleftarrow{\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\;\;} \shortmid} & {\textcolor{blue}{p} + \textcolor{red} {\Delta x}} & & \end{matrix} \, .
///////
Adapted to pullback of x = x(u):
///////
\, \begin{matrix} Y & {\xleftarrow{\;\;\;\;\;\;\;\;\;\; f \;\;\;\;\;\;\;\;\;\;}} & X & {\xleftarrow{\;\;\;\;\;\;\;\;\; x \;\;\;\;\;\;\;\;\;}} & U \\ \uparrow & & \uparrow & & \uparrow \\ f(x(u)) & \xleftarrow{\qquad \qquad \qquad}\shortmid & x(u) & \xleftarrow{\qquad \qquad \qquad}\shortmid & u \\ & & & & & & & \\ Y_{f(x(\textcolor{blue}{p}))} & {\xleftarrow{\;\;\;\;\;\;\;\;\; f_{x(\textcolor{blue}{p})} \;\;\;\;\;\;\;\;\;}} & X_{x(\textcolor{blue}{p})} & {\xleftarrow{\;\;\;\;\;\;\;\;\; x_{\textcolor{blue}{p}} \;\;\;\;\;\;\;\;\;}} & U_{\textcolor{blue}{p}} \\ \uparrow & & \uparrow & & \uparrow \\ & & {x(\textcolor{blue}{p}) + x'(u)_{\textcolor{blue}{p}} \, \textcolor{red} {\Delta u}} & {\xleftarrow{\;\;\;\;\;\;\;\;\; x_{\textcolor{blue}{p}} \;\;\;\;\;\;\;\;\;} \shortmid} & {\textcolor{blue}{p} + \textcolor{red} {\Delta u}} \\ f(x(\textcolor{blue}{p})) + {f'(x)}_{x(\textcolor{blue}{p})} \, \textcolor{red} {\Delta x} & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\; f_{x(\textcolor{blue}{p})} \;\;\;\;\;\;\;\;\;\;\;} \shortmid} & {x(\textcolor{blue}{p}) + \textcolor{red} {\Delta x}} & & \\ & & & & & \\ Y & & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; f \circ x \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}} & & U \\ \uparrow & & & & \uparrow \\ (f \circ x)(u) & & \xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid & & u \\ & & & & & & \\ Y_{f(x(\textcolor{blue}{p}))} & & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (f \circ x)_{\textcolor{blue}{p}} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}} & & U_{\textcolor{blue}{p}} \\ \uparrow & & & & \uparrow \\ {(f \circ x)(\textcolor{blue}{p}) + (f \circ x)'(u)_{\textcolor{blue}{p}} \, \textcolor{red} {\Delta u}} & & {\xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\shortmid} & & {\textcolor{blue}{p} + \textcolor{red} {\Delta u}} \end{matrix} \, .
///////
The Chain Rule for functions from \, \mathbb{R}^1 to \, \mathbb{R}^1 to \, \mathbb{R}^1 :
The basic diagram for an affine approximation of a function from \, \mathbb{R}^1 to \, \mathbb{R}^1
\, \begin{matrix} \mathbb{R}^1 & \xleftarrow{\qquad f \qquad} & \mathbb{R}^1 \\ \uparrow & & \uparrow \\ f(x) & \xleftarrow{\qquad \qquad}\shortmid & x \\ & & & & & \\ {\mathbb{R}^1}_{f(\textcolor{blue} {p})} & \xleftarrow{\;\;\;\; {f'(x)}_{\textcolor{blue}{p}} \;\;\;\; } & {\mathbb{R}^1}_{\textcolor{blue}{p}} \\ \uparrow & & \uparrow \\ df = {f'(x)}_{\textcolor{blue}{p}} dx & \xleftarrow{\qquad \qquad }\shortmid & dx \end{matrix} \, .
////
////
\, f(x(\textcolor{blue} {p})) + f'(x)_{x(\textcolor{blue} {p})} \, {x'(u)}_{\textcolor{blue} {p}} \, \textcolor{red} {\Delta u} \,
////
Expand the diagram to the right through the substitution x = x(u):
\, \begin{matrix} \mathbb{R}^1 & \xleftarrow{\qquad \qquad f \qquad \qquad} & \mathbb{R}^1 & \xleftarrow{\qquad \;\;\;\; x \;\;\;\; \qquad} & \mathbb{R}^1 \\ \uparrow & & \uparrow & & \uparrow \\ f(x(u)) & \xleftarrow{\qquad \qquad \qquad \qquad}\shortmid & x(u) & \xleftarrow{\qquad \qquad \qquad}\shortmid & u \\ & & & & & \\ {\mathbb{R}^1}_ {f(x(\textcolor{blue} {p}))} & \xleftarrow{{\qquad f'(x)}_{x(\textcolor{blue} {p})} \qquad} & {\mathbb{R}^1}_{x(\textcolor{blue} {p})} & \xleftarrow{\qquad x'(u)_{\textcolor{blue}{p}} \qquad} & {\mathbb{R}^1}_{\textcolor{blue}{p}} \\ \uparrow & & \uparrow & & \uparrow \\ df = {f'(x)}_{x(\textcolor{blue} {p})} \, dx & \xleftarrow{\qquad \qquad \qquad \qquad}\shortmid & dx = x'(u)_{\textcolor{blue}{p}} \, du & \xleftarrow{\qquad \qquad \qquad}\shortmid & du \\ & & & & & \\ {\mathbb{R}^1}_{f(x(\textcolor{blue} {p}))} & & \xleftarrow{\qquad \qquad \qquad (f \circ x)'(u)_{\textcolor{blue}{p}} \qquad \qquad \qquad} & & {\mathbb{R}^1}_{\textcolor{blue}{p}} \\ \uparrow & & & & \uparrow \\ d(f \circ x) = (f \circ x)'(u)_{\textcolor{blue}{p}} \, du = {f'(x)}_{x(\textcolor{blue} {p})} \, x'(u)_{\textcolor{blue}{p}} \, du & & \xleftarrow{\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad}\shortmid & & du \end{matrix} \,
///////
x = x(u):
\, x(\textcolor{blue} {p} + \textcolor{red} {\Delta u}) = x(\textcolor{blue}{p}) + \textcolor{blue} {x'(\textcolor{black} {u})_p} \textcolor{red} {\Delta u} + o( | \textcolor{red}{\Delta u} | ) \, .
f(x) = f(x(u)) :
\, f(x(\textcolor{blue}{p} + \textcolor{red}{\Delta u})) = f(x(\textcolor{blue}{p})) + {f'(x)}_{x(\textcolor{blue}{p})} \, {x'(u)}_{\textcolor{blue}{p}} \, \textcolor{red}{\Delta u} + o( | \textcolor{red} {\Delta u} | ) \, .
///////
A movie of the chain rule for functions from \, \mathbb{R}^1 to \, \mathbb{R}^1 to \, \mathbb{R}^1
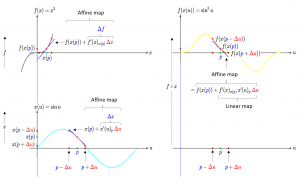
Example:
Light-blue curve (bottom left window): x(u) = \sin u.
Derivative: x'(u) = \cos u
Black curve (top left window): f(x) = x^3.
Derivative: f'(x) = 3 x^2
Yellow curve (top right window): (f \circ x) (u) = f(x(u)) = (\sin u)^3.
Derivative: (f \circ x)'(u) = f'(x(u)) \, x'(u) = 3 x(u)^2 \, x'(u) = 3 (\sin u)^2 \cos u.
///////
The interactive simulation that created this movie
///////