This page is a sub-page of our page on Mathematical Concepts.
///////
Vedic Mathematics at Wikipedia
Vedic Mathematics by Bharati Krishna Tirtha
/////// Quoting Wikipedia on “Vedic Mathematics”:
Vedic Mathematics is a book written by the Indian monk Bharati Krishna Tirtha, and first published in 1965. It contains a list of mathematical techniques, which the author stated were retrieved from the Vedas and supposedly contained all mathematical knowledge.
These statements have been since rejected in their entirety [1]
Krishna Tirtha failed to produce the sources, and scholars unanimously note it to be a mere compendium of tricks for increasing the speed of elementary mathematical calculations with no overlap with historical mathematical developments during the Vedic period.
However, there has been a proliferation of publications in this area and multiple attempts to integrate the subject into mainstream education by right-wing Hindu nationalist governments.
[…]
STS scholar S. G. Dani in ‘Vedic Mathematics’: Myth and Reality [2] states that the book is primarily a compendium of tricks that can be applied in elementary, middle and high school arithmetic and algebra, to gain faster results. The sutras and sub-sutras are abstract literary expressions (as “much less“, “by one less than the previous one” et al.) prone to creative interpretations; Krishna Tirtha exploited this to the extent of manipulating the same shloka to generate widely different mathematical equivalencies across a multitude of contexts. [2]
[…]
Dani points out that the contents of the book have “practically nothing in common” with the mathematics of the Vedic period or even with subsequent developments in Indian mathematics. [2]
K. S. Shukla reiterates the observations, on a per-chapter basis. [4] For example, multiple techniques in the book involve the use of high-precision decimals. These were unknown during the Vedic times and were introduced in India only in the sixteenth century; [3] works of numerous ancient mathematicians such as Aryabhata, Brahmagupta and Bhaskara (commonly called Bhaskara I to avoid confusion with the 12th-century mathematician Bhāskara II) were entirely based on fractions. [2]
Some of the sutras of Krishna Tirtha even run parallel to the General Leibniz rule and Taylor’s theorem (which, per Krishna Tirtha, were to be yet studied by the western world during the time of his writing) but did ultimately boil down to the sub-elementary operations of basic differentiation on polynomials.
From a historiographic perspective, India had no minimal knowledge about the conceptual notions of differentiation and integration. [2] Sutras have been further leveraged that analytic geometry of conics occupied an important tier in Vedic Mathematics, which runs contrary to all available evidence. [2][3]
[…]
Dani notes the book to be of dubious quality. He believes it did a disservice both to the pedagogy of mathematical education by presenting the subject as a bunch of tricks without any conceptual rigor, and to science and technology studies in India (STS) by adhering to dubious standards of historiography. [2][a]
Dani also points out that while Tirtha’s system could be used as a teaching aid, there was a need to prevent the use of “public money and energy on its propagation” except in a limited way and that authentic Vedic studies were being neglected in India even as Tirtha’s system received support from several government and private agencies. [2] Jayant Narlikar has voiced similar concerns. [9]
Hartosh Singh Bal notes that whilst Krishna Tirtha‘s attempts might be somewhat acceptable in light of his nationalistic inclinations during colonial rule.
Since Krishna Tirtha had left his spiritual endeavors to be appointed as the principal of a college, set up during the British Raj to counter Macaulayism, his book set the grounds for further ethno-nationalistic abuse of historiography by Hindu Nationalist parties; Thomas Trautmann views the development of Vedic Mathematics in a similar manner. [5][10]
Others have viewed the works as an attempt at harmonizing religion with science. [11]
Meera Nanda has noted hagiographic descriptions of Indian knowledge systems by various right-wing cultural movements (including the BJP), which deemed Krishna Tirtha to be in the same league as Srinivasa Ramanujan. [12] In an article she wrote for Open magazine, Nanda observes that the sutras of Atharvaveda on which Swami Shri Bharti Krishna has apparently based his theory of Vedic mathematics are not there in the Atharvaveda at all. [13]
Some have however praised the methods of Vedic mathematics and commented on their potential to attract school-children to mathematics and increase popular engagement with the subject. [14][15][16]
Originality of methods
Dani believes Krishna Tirtha‘s methods to be a product of his academic training in mathematics [b] and his long recorded habit of experimentation with numbers; nonetheless, he considers the work to be an impressive feat. [2] Similar systems include the Trachtenberg system or the techniques mentioned in Lester Meyers’s 1947 book High-speed Mathematics. [2]
Alex Bellos points out that several of the calculation tricks can also be found in certain European treatises on calculation from the early Modern period. [17]
Integration into mainstream education
The book Vedic Mathematics had been included in the school syllabus of Madhya Pradesh and Uttar Pradesh, soon after the Bharatiya Janata Party (BJP), a right-wing Hindu nationalist political party came to power and chose to saffronise the education-system. [7]:6 [12][23][24]
Dinanath Batra had conducted a lengthy campaign for the inclusion of Vedic Maths into the National Council of Educational Research and Training (NCERT) curricula. [25] Subsequently, there was a proposal from NCERT to induct Vedic Maths, along with a number of fringe pseudo-scientific subjects (Vedic Astrology et al.), into the standard academic curricula.
This was only shelved after a number of academics and mathematicians, led by Dani and sometimes backed by political parties, opposed these attempts based on previously discussed rationales and criticized the move as a politically guided attempt at saffronisation. [3][26][27][28][29][30]
Concurrent official reports also advocated for its inclusion in the Madrassah education system to modernize it. [31]
After the BJP‘s return to power in 2014, three universities have begun to offer courses on the subject while a television channel, catering to the topic, was also launched; generous education and research grants have also been allotted to the subject. [32][33][34][35]
/////// End of quote from Wikipedia
/////// Quoting from the book “Vedic Mathematics“ (p. 196)
Chapter XXVI: RECURRING DECIMALS
It has become a sort of fashionable sign of cultural advancement, not to say up-to-datism, for people now-a-days to talk not only grandly but also grandiosely and grandiloquently about Decimal coinage, Decimal weights, Decimal measurements etc.; but there can be no denying or disguising of the fact that the western world as such – not excluding its mathematicians, physicists and other expert scientists – seems to have a tendency to theorise on the one hand on the superiority of the decimal notation and to fight shy, on the other, in actual practice – of decimals and positively prefer “vulgar fractions” to them!
In fact, this deplorable state of affairs has reached such a pass that the mathematics syllabus – curricula in the schools, colleges and universities have been persistently “progressing” and “advancing” in this wrong direction to the extent of declaring that Recurring decimals are not integral parts of the matriculation course in mathematics and actually instructing the pupils to convert all recurring decimals AT SIGHT into their equivalent vulgar fraction shape, complete the whole work with them and finally re-convert the fraction result back into its decimal shape!
///////
(p.203):
We pass now on to still another and easier method which comes under the Ekadhika Sutra which we have expounded and explained at sufficient lenth already (in the first chapter) and which therefore we need only summarise and supplement here but not elaborate again.
The Ekadhika Sutra (which means ‘by the preceding one increased by one’) has already been shown at work in a number of ways and in a number of directions an on a number of occasions and will similarly come into operation still further, in many more ways and in many more contexts.
[Dividing with] Numbers ending in nine
(i) If and when the last digit of the denominator is 9, we know beforehand that the equivalent recurring decimal ends in 1. [cf. p. 3)
(ii) In the case of 1/19, the last-but-one digit is 1; we increase it by 1 and make it 2. In 1/29 we work with 2 + 1 = 3. In 1/39 and 1/49 we operate with 4 and 5 respectively, and so on.
(iii) In the multiplication process (Ekadhika Purva), in all these cases, we put 1 down as the last digit (i.e. in the right-hand-most place): and we go on multiplying that last digit (1) from the right towards the left by 2, 3, 4, and 5 respectively; and when there is more than one digit in that product, we set the last of those digits down there and carry the rest of it over to the next immediately preceding digit towards the left.
(iv) When we get to digit = N-1 (while computing the recurring decimals for 1/N where N = 1, 2, 4), we know that we have done half the work. We then stop the multiplication there and we mechanically put down the remaining half of the answer (by merely taking the complements from NINE)
(p.205):
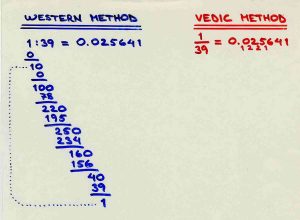
(3) Next let us take 1/39.
Take 1 again at the extreme right end and continually multiply by 3 + 1 = 4 from the right to the left. Thus we have 1/39 = .025641. Note that in this case 39 is a multiple of 3 and 13 and not a prime number (like 19 and 29) and since (nabla-dot) 3 and 13 give only 1 respectively 6 recurring decimals, there is a difference in its behaviour i.e. that the two halves are not complementary with respect to 9 but only in relation to 6! In fact N-1 (i.e. 38) does not come up at all as an interrim product (as 18 and 28 did). And so, the question of complements from 9 does not arise at all; and the decimal equivalent has only 6 figures (and not 38)!
The reason for this is very simple. As 1/39 = (1/13)/3, as 1/13 has only 6 recurring decimals in its decimal equivalent and because, for reasons to be explained a little later, this decimal equivalent of 1/13 is exactly divisible by 9, much more, therefore, it is divisible by 3.
And, consequently, when we divide it by 3 and exhaust the six digits, we find that there is no remainder left. In other words, 1/39 has only 6 digits in its recurring decimal shape. These have been obtained by the same Ekadhika process that served our purpose in the case of 1/19 and 1/29.
We next take up the and examine the case of 1/49 which, besides following the rules hereinabove explained, has the additional merit of giving us the clue to a still easier process for the conversion of vulgar fractions into their recurring decimal shape:
1/49 = 1/(7×7) = (.142857)/7
/////// End of quote from the book “Vedic Mathematics“
///////
///////
///////
///////
///////
///////