This page is a sub-page of our page on Time.
///////
Related sources of information:
The Expansion of Time into a Laurent Series of Moments:
///////
L_{aurent}(T_{ime}) \equiv {\sum\limits_{n \in \mathbb{Z}}^{ \text {} }} N_{ow}^n \equiv {\sum\limits_{n < 0}^{ \text {} }} N_{ow}^n + N_{ow}^0 + {\sum\limits_{n > 0}^{ \text {} }} N_{ow}^n \equiv P_{ast} + N_{ow} + F_{uture} \equiv \,
\equiv \cdots + N_{ow}^{-3} + N_{ow}^{-2} + N_{ow}^{-1} + N_{ow}^0 + N_{ow}^1 + N_{ow}^2 + N_{ow}^3 + \cdots \equiv \,
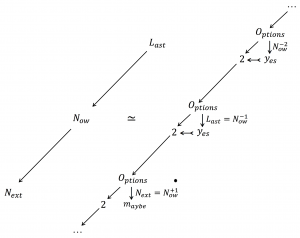
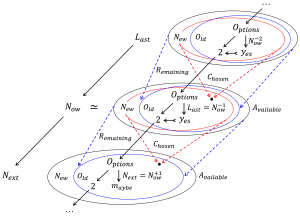
\equiv P_{ast}(L_{ast}) + L_{ast} + N_{ow} + N_{ext} + F_{uture}(N_{ext}) \, .
\int L_{aurent}(T_{ime}) \equiv \cdots + \int N_{ow}^{-2} + \int N_{ow}^{-1} + \int N_{ow}^0 + \int N_{ow}^1 + \int N_{ow}^2 + \cdots \, \equiv
\equiv \cdots + N_{ow}^{-1} + \log N_{ow} + N_{ow}^1 + N_{ow}^2 + N_{ow}^3 + \cdots \, .
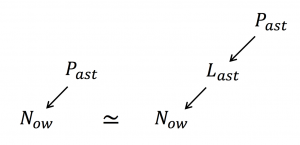
R_{esidue}(L_{aurent}(T_{ime})) \equiv L_{ast} \equiv N_{ow}^{-1} \, .
///////
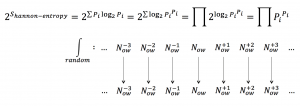
Shannon entropy leads to frequentism:
2^{\, S_{hannon-entropy}} = 2^{\; \sum {P_i \log P_i}} = 2^{\; \sum {\log {P_i}^{P_i}}} = \prod {P_i}^{P_i} \, .
Historic entropy leads to Bayesianism:
2^{\, H_{istoric-entropy}} = 2^{\; \sum {P_{i-1} \log P_i}} = 2^{\; \sum {\log {P_i}^{P_{i-1}}}} = \prod {P_i}^{P_{i-1}} \, .
///////
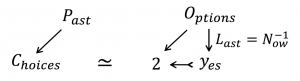
{\int\limits_{n \in \mathbb{Z}}^{ \text {} }} N_{ow}^n = \int N_{ow}^{-1} = \log N_{ow} \, .
N_{ow} \equiv 2^{\; \log N_{ow}} = 2^{\; \; \int\limits_{c_{hoices}^{ \text {} }} N_{ow}^{-1}}.
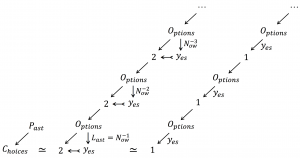
N_{ow} \equiv 2^{\; \log N_{ow}} = 2^{\; \int N_{ow}^{-1}} = 2^{\; \int 2^{\; \int N_{ow}^{-2}}} = 2^{\; \int 2^{\; \int 2^{\; \int N_{ow}^{-3}}}} = \cdots \, .
///////
The Now raised to the power of the Past:
The Choices are made at the Last moment:
The Choices of the Past are closed:
The Choices of the Future are still open:
Options Choice chain complex:
///////
The now is transforming the Next into the Past:
The now acts on the future by choosing from its available options
based on its comprehension of its actions and reactions from the past.