This page is a sub-page of our page on Entropy.

///////

Related KMR-pages:

• Shannon Entropy
• Historic Entropy
• BioEntropy
• Laurent expansion of Time

///////

Other relevant sources of information:

• Category Theory
• Topos
• Subobject classifier
• Gregory Bateson

///////

The power of thinking is knowing what not to think about:

\, {T_{hinking}}^{P_{ower}} \, = \, \{ \, f \, : \, P_{ower} \, \xrightarrow[ \; no \; ]{ \; yes \; } \, T_{hinking} \, = \, \{ \, f \, : \, P_{ower} \, \xrightarrow[ \; disregard \; ]{ \; focus \ on \; } \, T_{hinking}\, \} \, [ \, {T_{hinking}}^{\bold{2}} \, ]_{R_{elations}} \, \mapsto \, \left< \, B_{inary} \, T_{hinking} \, \right>_{R_{elations}} \, \mapsto \, \left< \, m_{ultigraph} \, \right>_{R_{elations}} \, \, [ \, {T_{hinking}}^{\bold{3}} \, ]_{R_{elations}} \, \mapsto \, \left< \, T_{ernary} \, T_{hinking} \, \right>_{R_{elations}} \, \mapsto \, \left< \, h_{ypergraph} \, \right>_{R_{elations}} \, \, [ \, {T_{hinking}}^{\bold{\Omega}} \, ]_{R_{elations}} \, \mapsto \, \left< \, E_{volutionary} \, T_{hinking} \, \right>_{R_{elations}} \,

<p>

Evolutionary entropy 1:

Options-generating function:

Evolutionary entropy 2:

Evolutionary entropy 3:

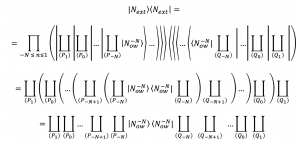
By including the \, N_{ext} \, term which corresponds to \, i = i \,
we have

/////////