This page is a sub-page of our page on Mathematical Concepts
///////
Related KMR-pages:
• The Linear War between the planets \, V_{ectoria} \, and \, V'_{ectoria} \,
• Einstein for Flatlanders
• Einstein for Linelanders
• Tesseracts for Flatlanders
• Non-Euclidean Geometry
• Oscar Reutersvärd
• M.C. Escher
• Disambiguation
• Entropy
• Function
• Homology and Cohomology
• Homotopy
• Space
• Time
• Products
• Quotients
• Topos
• Duality
• Topology
• Uncertainty
• Dimension
///////
Other relevant sources of information:
• Flatland – the movie 2007, based on the novel Flatland by Edwin A. Abbott from 1884.
• Flatland – the limit of our consciousness
• Tesseracts
• And he built a crooked house, by Robert A. Heinlein
• Corpus Hypercubus by Salvador Dali
• What would a 4D-sphere look like in real life?
• A Wrinkle In Time, 2018 Disney film based on the novel by Madeleine L’Engle from 1962.
• How mathematicians are storytellers and numbers are the characters
Marcus du Satoy in The Guardian, 23 January 2015.
• Duality
• A Mathematician’s Lament by Paul Lockhart.
///////
The interactive simulations on this page can be navigated with the Free Viewer of the Graphing Calculator.
///////
In Swedish: [Utdrag ur en chatt med Erik Isaksson den 16 april 2020]:
Jag tänker mig att “geometrikursen” i MTV ska bygga på att lära sig att tolka 2D och 3D skuggor från enkla rörelser av olika matematiska former. Och att teamet bedriver “reverse engineering” på dessa skuggor för att lista ut hur de uppkommer. Det är min övergripande inlärningsprincip för MTV. Några av mina senaste videos på YouTube handlar om sådant material.
Erik: Omvänd Platons grotta?
Bra metafor! Man skulle kunna säga att det var denna omvändning som intresserade Sokrates. Han gav inga svar, utan han ställde hela tiden frågor. Frågor som fick hans samtalsparters att omvärdera sina utgångspunkter.
Det är detta som är så oerhört svårt: Att verkligen se och känna sina egna “utgångspunkter.” David Hilbert sa en gång: “De flesta människors tankar rör sig i en cirkel med radie noll – och denna kallar de sin ståndpunkt.”
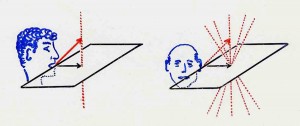
Tänk på skillnaden mellan att modellera vridningen av din arm runt en axel (behöver tre parametrar) och att modellera skuggan av denna vridning på väggen eller golvet. Det är enkelheten i rörelsebeskrivningarna som är den största belöningen med att “gå uppåt i dimension.”
Det finns en mycket vacker matematisk sats som säger att
varje icke-expansiv avbildning \, { \mathbb{R}}^n \rightarrow { \mathbb{R}}^n \, kan beskrivas som en skugga
av en isometri (stel rörelse) \, { \mathbb{R}}^m \rightarrow { \mathbb{R}}^m \, där \, m \, högst lika med \, 2n + 1 .
Dvs om en avbildning inte “flyttar isär” något par av punkter i \, { \mathbb{R}}^n \,
så kan den beskrivas som skuggan av en isometri i \, { \mathbb{R}}^m \, .
Att lyckas i MTV kommer till stor del att handla om att hitta de isometrier som ligger bakom de skuggor som teamet iakttar på sin rymd-odyssé.
Om man “specar” på denna nivå tror jag man kan få med sig den “långa svans” som är beredda att lägga egen tid på att skapa sådana situationer. Lite som schackproblem eller sudoku.
Teamet bygger ökad förståelse av mångdimensionell matematik genom att testa olika typer av projektioner och jämföra deras skuggor med dem som de observerar i det skuggfenomen som de försöker “knäcka”.
Erik: Intressant “use case” för verktyg i en geometriaktivitet i ett space.
Augmented geometry
Augmented geometric performance
Här skulle vi kunna försöka få till ett studentprojekt.
Erik: Om jag skulle ha en plattform och miljö klar för sådana verktyg så skulle nog ett studentprojekt kunna funka. Borde vara realistiskt till sent på hösten.
/////// Back to English:
What does the word “dimension” mean?
In mathematics
the word “dimension”
refers to “independent direction” in geometry
and “independent combination” in combinatorics,
ring theory, or module theory.
If something represents “a new dimension”
then that something cannot be represented
as a combination of “other things”
in the collection of things
that is tacitly assumed to exist
when we use the word “new” above.
In fact, these “other things”
represent the “other dimensions”
that we assume to be already present
when we add a “new dimension.”
///////
The determinant as a measure of volume:
1D-volume = length (of a distance)
2D-volume = area (of a surface)
3D-volume = volume (of a body)
…
nD-volume = nD-volume (of a body in an nD vector space)
///////
Codimensional geometry
is the key to understanding
higher-dimensional geometry
The line
has dimension one
and codimension one
in two-dimensional space
The plane
has dimension two
and codimension one
in three-dimensional space
The line
has dimension one
and codimension two
in three-dimensional space
The point
has dimension zero
and codimension three
in three-dimensional space
The space
has dimension \, \mathbf {n}
and codimension zero
in \, \mathbf {n} -dimensional space
The hyperplane
has dimension \, \mathbf {n-1}
and codimension one
in \, \mathbf {n} -dimensional space
The hyperline
has dimension \, \mathbf {n-2}
and codimension two
in \, \mathbf {n} -dimensional space
The hyperpoint
has dimension \, \mathbf {n-3}
and codimension three
in \, \mathbf {n} -dimensional space
TERMINOLOGY: The terms ‘hyperline’ and ‘hyperpoint’ are not standard – as opposed to the term ‘hyperplane’. ‘Hyperline’ and ‘hyperpoint’ are used here in order to emphasize their codimensional relationships to the terms ‘line’ and ‘point.’
///////
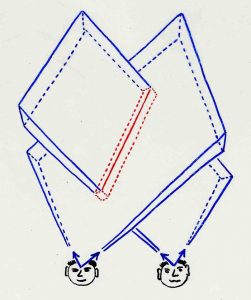
Intersecting the diagonal of a 3D-cube (left) and a 4D-cube (right)
with a perpendicular hyperplane (Ambjörn Naeve on YouTube)
Higher-dimensional cubes and their shadows in 3D-space
///////
A Triact (3D-cube) is a Tesseract for Flatlanders
(Ambjörn Naeve on YouTube):
The interactive simulation that produced this movie.
This movie shows a 3D-Cube as a HyperSquare (= Triact) casting its shadow onto Flatland (= 2D-Space).
A rotating 3D-Cube can be projected onto 2D-Space from a 3D-Point outside of this 2D-Space. This produces the “inside-out” turning motions of its shadows in 2D-Space.
Analogously we can regard the 4D-Cube as a HyperCube (= Tesseract) casting its shadow onto 3D-Space.
A rotating 4D-Cube can be projected onto 3D-Space from a 4D-Point outside of this 3D-Space. This produces the “inside-out” turning motions of its shadows in 3D-Space.
Notice how the simple rotational motion of the Triact in 3D is transformed into a much more complicated transformation of its shadow in 2D. In the same way, the simple rotational motion of the Tesseract in 4D is transformed into a much more complicated transformation of its shadow in 3D.
///////
A rotating Tesseract (4D-cube) projected into 3D-space
(throughthedoors on YouTube):
///////
A rotating Penteract (5D-cube) projected into 3D-space
(hypercube0 on YouTube):
///////
A rotating Hexeract (6D-cube) projected into 3D-space
(WildStar2002 on YouTube):
///////
Unwrapping a tesseract (4d cube aka hypercube)
(Vladimir Panfilov on YouTube):
///////
The Scan of a Tesseract in 4-dimensional space:
(Визуализации в многомерных пространствах on YouTube)
Quoting from the text of this video: The first part of the video shows a scan of the usual three-dimensional cube as it collapsed and expanded. In the second part, the same thing is happening with four-dimensional cube (a tesseract) in four-dimensional space. First the tesseract loses its transparency, then it again gets.
Consider the standard Cartesian coordinate system \, Owxyz \, in four-dimensional space \, V . Consider \, V \, a tesseract centered at the point \, (500, 0, 0, 0) \, and side \, 200 . Give its two-dimensional faces color so that during the folding of the tesseract matched faces have the same color.
Install a four-dimensional camera at the origin with a distance of \, 100 \, to the projected three-dimensional space \, U . Define the direction of the camera in the direction of \, w -axis.
Set in \, U \, a three-dimensional camera at the point \, (1100 \sin(2πt/10), 1100 \cos(2πt/10), 550 \sin(2πt/7.1)) \, with the direction to the origin of the \, U \, space and with the distance to the projection plane \, 100 \, and draw a dot-projected tesseract at the \, U \, of \, V \, with the centre of projection coinciding with the four-dimensional position of the camera.
Start to collapse and expand the tesseract. This will produce what is shown in the video.
///////
THE SIXTH PLATONIC SOLID
The sixth Platonic Solid is called the 120-cell.
It consists of 120 dodecahedrons interconnected in 4D-Space:
120-cell rotating in 4D
(Rob Scharein on YouTube):
///////
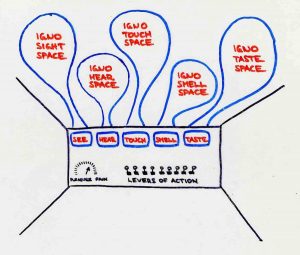
Reverse engineering of our experiences
with the phenomenon of shape-changing surfaces
induces the third dimension
as the simplest way to synesthesize
the partially blocked phenomena that we experience.
///////
///////
///////
///////
///////
///////
///////
///////
///////
///////
///////
///////
///////