A Dramatic New Look at the Creative Roots of Science and Life
///////
Coloring text in HTML:
Text
///////
This page is a sub-page of our page on Physics and its Models
///////
Most of the material on this page consists of quotes from the book:
Science, Order, and Creativity – A Dramatic New Look at the Creative Roots of Science and Life, by David Bohm and F. David Peat, Bantam Books, 1987.
However, important concepts that are described in the text have been linked to suitable sources on the web, mostly to Wikipedia.
///////
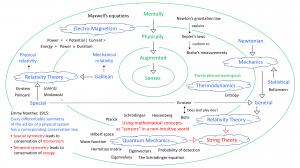
Physically and mentally augmented senses
///////
Anchors into the text below:
• Fragmentation and Change in Science
• Novelty and Conservation in Scientific Theories
• Creativity and Metaphors
• Hamilton-Jacobi Theory
• Similarities and Differences: Heisenberg’s and Schrödinger’s Approaches to the Quantum Theory
• Chapter 2: SCIENCE AS CREATIVE PERCEPTION-COMMUNICATION
• Perception Through the Senses and through the Mind
• Communication is Essential to Perception in Science
• Metaphors as Ways of Healing Breaks in Communication
• Language in Science
• The Bohr-Einstein Dialogues and the Breakdown of Communication in Physics
•
•
///////
/////// Quoting Bohm and Peat:
INTRODUCTION
[p.7]
DAVID PEAT: But on the other hand, many of the deepest scientific thinkers have used criteria of mathematical beauty in the development of their theories. They believed that the deepest scientific explanations must also be mathematically beautiful. Without the requirement of mathematical aesthetics a great many discoveries would not have been made. Surely in your own work the criteria of mathematical elegance must have acted as a signpost that you were on the right track?
DAVID BOHM: Certainly mathematics gives rise to creative insights, and the search for mathematical beauty can be a helpful guide. Scientists who have worked in this way have often been successful in deriving new knowledge through an emphasis on the mathematical formalism. I have already mentioned Kepler and Heisenberg, and in modern times I could add such names as Dirac, von Neumann, Jordan, and Wigner. But mathematics was never sole criterion in their discoveries. Moreover, this does not mean that everyone thinks alike in this regard. In fact, I think that verbal concepts, pictorial aspects, and philosophical thinking can contribute significantly to new ideas. Einstein certainly appreciated mathematical beauty very keenly but he did not actually begin from the mathematics, especially in his most creative period. Instead, he started with unspecifiable feelings and a succession of images out of which more detailed concepts eventually emerged. I would go along with this and add that ideas arising in this way, or in other ways, may eventually lead to further mathematical developments and even to the suggestion of new forms of mathematics.
It seems arbitrary to say that mathematics must play a unique role in the expression of reality. Mathematics is only one function of the human mind, and other functions can surely be just as important – even in physics.
DAVID PEAT: This dialogue is moving in an interesting direction. We seem to be saying that physics may have taken a wrong direction in giving so much emphasis to its formalisms. But I’m sure that many scientists would point out that mathematics happens to be the most abstract and logically coherent way of thinking that is known to us. It seems to be totally open to free creation and not bounded by the requirements of sense experiences of ordinary reality. Doesn’t that give it a unique status?
DAVID BOHM: Well, in reply I’d like to bring in the work of Alfred Korzybski, an American philosopher who was fairly well known in the early twentieth century. He said that mathematics is a limited linguistic scheme, which makes possible great precision and coherence – but at the expense of such extreme abstraction that its applicability has, in certain key ways, to be bounded.
Korzybski said, for example, that whatever we say a thing is, it isn’t. First of all, whatever we say in words, and what we want to talk about is generally not words. Second, whatever we mean by what we say is not what the thing actually is, though it may be similar. For the thing is always more than what we mean and is never exhausted by our concepts. And the thing is also different from what we mean, if only because no thought can be absolutely correct when it is extended indefinitely. The fact that a thing has qualities going beyond whatever we think and say about it is behind our notion of objective reality. Clearly, if reality were ever to cease to show new aspects that are not in our thought, then we could hardly say that it had an objective existence independent of us.
All this implies that every kind of thought, mathematics included, is an abstraction, which does not and cannot cover the whole of reality. Different kinds of thought and different kinds of abstraction may together give a better reflection of reality. Each is limited in its own way, but together they extend our grasp of reality further than is possible with one way alone.
DAVID PEAT: What you have said about Korzybski reminds me of René Magritte‘s painting of a pipe which also contains the words This is not a pipe. However realistic a painting may be, it falls indefinitely short of being an actual pipe. And ironically, the word pipe in the title is not an actual pipe either. Perhaps, in the spirit of Magritte, every theory of the universe should have in it the fundamental statement “This is not the universe.”
================================
Hom-O-Sapiens = Hom(Universe, Mind)
Mathematics is the study of all structures
that the human mind is able to perceive.
List of mathematical jargon
================================
DAVID BOHM: Actually, a theory is a kind of map of the universe, and like any other map, it is a limited abstraction and not entirely accurate. Mathematics provides one aspect of the overall map, but other ways of thinking are needed along the lines we have been discussing.
DAVID PEAT: Well, it’s certainly true that in the early days of quantum theory, leading physicists like Bohr, Heisenberg, Pauli, Schrödinger, and de Broglie were vitally concerned with philosophical questions, especially on the relationship between ideas and reality.
DAVID BOHM: These questions go beyond the limited scope of physics as it is generally known today. Each of these thinkers approaches the problem in his own way and there are important and subtle differences between them that we tend to overlook today. But the general practice of physics has indeed become remote from these deeper considerations. It tends to concentrate on technical questions, and for this reason, it seems to have lost contact with its own roots. For example, in any attempt to unify quantum mechanics and relativity, especially general relativity, there are fundamental questions that must be faced. How can physicists hope to work successfully in this field when they ignore the subtle and unresolved problems that still lie buried in the early period of quantum mechanics?
DAVID PEAT: I remember that these sorts of questions kept coming up in the discussions we had together at Birbeck College. We were especially concerned with the narrowness of vision that is developing, not only in physics, but quite generally in scientific research.
DAVID BOHM: We used an analogy from human vision. The details of what we see are picked up in a small central part of the retina called the fovea. If this is destroyed, then the detailed vision is lost, but general vision, which comes from the periphery of the retina, remains. But if the periphery is damaged, while the fovea remains intact, even the details lose all their meaning. By analogy, we asked if science was in danger of suffering a similar “damage” of its vision. By giving so much emphasis on mathematics, science seems to be losing sight of the wider context of its vision.
DAVID PEAT: But originally there was such a general vision of the universe, humanity, and our place in the whole. Science, art, and religion were never really separate.
DAVID BOHM: But as time went on, this vision changed with specialization. It grew progressively narrower and eventually led to our present approach, which is, in large part, fragmentary. I think this development partly arose because physics had become the pattern or ideal toward which all the sciences aim. While most sciences are not as dominated by mathematics, the essential point is the spirit in which mathematics tends to be done. Its general aim is to try to analyze everything into independent elements that can be dealt with separately. This encourages the hope that any problem can be split off into a separate fragment.
Now, it is still true that science also contains a movement toward synthesis and to discovering broader contexts and more general laws. But the prevailing attitude has been to put the major emphasis on analysis and on splitting off the key factors of each situation. Scientists hope that this will enable them to extend their powers indefinitely to predict and control things.
DAVID PEAT: It’s important to emphasize that not only is this sort of approach fundamental to physics, but it also extends into chemistry, biology, the neurosciences, and even into economics and psychology.
DAVID BOHM: By concentrating on this sort of analysis and constantly splitting off problems into specialized areas, we increasingly ignore the wider context that gives things their unity. In fact, this spirit is now spreading beyond science, not only into technology, but into our general approach to life as a whole. Understanding is now valued as the means to predict, control, and manipulate things. Of course, beginning with Francis Bacon, this has always been important, but never so dominant as today.
DAVID PEAT: Yes, science has been moving at an ever-increasing rate since the nineteenth century and it’s bringing with it a host of technological changes. But it is only relatively recently that so many people have begun to question if all this progress is really beneficial. We’re beginning to realize that the cost of progress is more and more specialization and fragmentation to the point where the whole activity is losing its meaning. I think that the time has come for science to pause and take a careful look at where it is going.
DAVID BOHM: I think that even more than this we need to change what we mean by “science.” The moment has come for a creative surge along new lines. This is essentially what we are proposing in Science, Order, and Creativity.
DAVID PEAT: But most scientists would be shocked by such a suggestion. After all, it must look as if science has never been more active and successful than it is today. In every field there are new frontiers opening up and new technologies are being exploited. Think of all those novel experimental techniques, exiting new theories, and interesting problems for an indefinite number of research workers to tackle. Take medicine, for example: So many diseases have been wiped out and there is the promise of eradicating even more. And there are the new fields of biotechnology and genetic engineering, and let’s not forget the changes that are being made by computers and mass communication. In every area of life, science is making a really powerful impact.
DAVID BOHM: All this is true, but some very important factors have been neglected in obtaining such progress. First of all, there has been an overall fragmentation in our general attitude to reality. This leads us to focus always on particular problems, even when they are significantly related to a broader context. As a result, we fail to notice the unforeseen negative consequences, which cannot always be dealt with in terms of a fragmentary mode of thought. The result is that these difficulties spread into the whole context and eventually come back to create problems that may be worse than those we started with. For example, by exploring natural resources in a fragmentary manner, society has brought about the destruction of forests and agricultural lands, created deserts, and even threatens the melting of the ice caps.
DAVID PEAT: I remember looking into the whole question of the development of more productive strains of crops. It’s not at all clear that they have been totally beneficial. To begin with, it leads to the problem of the great vulnerability of a limited genetic strain, and there is an increased reliance on fertilizers, pesticides, herbicides, and ripeners. When you take all this, together with the more efficient farming techniques that these new crops require, it produces radical changes in agrarian societies that have to rely more and more in an industrial basis. In the end, the whole society changes in an uncontrolled way and its economy becomes dependent on imports and it is vulnerable to global instabilities.
DAVID BOHM: Of course, many people think that solving these sorts of problems is only a matter of studying ecology or some other speciality. Certainly ecology does begin to acknowledge the complex dependence of each activity on the whole context. But really the problem is as much one of economics as it is of ecology, and this leads on to politics, and to the structure of society and the nature of human beings in general.
The key issue is this: How is it possible to subject all these factors to prediction and control in order to manipulate the system and bring about good order? Clearly this is an impossible demand. To begin with, there is the infinite complexity involved, and the extreme instability of these systems, which requires almost perfect and, probably unattainable, degrees of control.
But more important, the system itself depends on human beings. And how can science lead human beings to control themselves? How do scientists propose to control hatred between nations, religions, and ideologies when science itself is fundamentally limited and controlled by these very things? And what about the growing psychological tension in a society that is so unresponsive to human needs that life seems, for many, to have lost its meaning? In the face of all this, some people break down mentally, or become dependent on various drugs, while others engage in mindless violence.
DAVID PEAT: It seems impossible to dream that through some sort of new discovery in chemistry or biology or the behavioral sciences that all these problems will ever be brought under control. They are so far-reaching and pervasive. How does science intend to end the danger of mutual annihilation that exists in the world? After all, this has its origin in the fear, mistrust, and hatred between nations. It seems to me that the more science and technology develops, the more dangerous the whole situation is becoming.
DAVID BOHM: Of course, a century or so ago the benefits from science generally outweighed the negative effects, even when the whole endeavor was carried out without regard for long-range consequences. But the modern world is finite and we have almost unlimited powers of destruction. It’s clear that the world has passed a point of no return. This is one reason why we have to pause and consider the possibility of a fundamental and extensive change in what science means to us.
DAVID PEAT: What we need is not so much new scientific ideas, although these are still going to be of great interest. The question is how can science, when it is based on a fragmentary attitude to life, ever understand the essence of real problems that depend on an indefinitely wide context? The answer does not lie in the accumulation of more and more knowledge. What is needed is wisdom. It is a lack of wisdom [phronesis] that is causing most of our serious problems rather than a lack of knowledge.
DAVID BOHM: But this also implies goodwill and friendliness. This seems to be lacking today, among scientists as much as in the general public.
DAVID PEAT: Of course, goodwill and friendliness are important if people are going to work together for the common good. But in the long run, I think that we may have to sacrifice some of the values that we hold so dear today. For example, we have to question the indefinite increase of individual comfort and prosperity and the preeminence of the competitive spirit, which is basically divisive and fragmentary.
DAVID BOHM: Yes, and it’s arbitrary to forever limit science to what it has become today. After all, this was the result of a historical process that involved many fortuitous elements. We have to explore in a creative way what a new notion of science might be, a notion that is suitable for our present time. This means that all the subjects that we have been talking about will have to come into the discussion.
DAVID PEAT: I think that if we are to understand this call for a new creative surge in science, then we also have to understand the historical perspective that you’ve been talking about. We need to understand how our present fragmentary approach came about. For example, it would be interesting to think about what would have happened if different pathways that were available at the time had been fully explored in the past.
DAVID BOHM: But these sorts of discussions cannot be restricted to science alone. We have to include the whole range of human activities. Our aim is to throw light on the nature of creativity and how it can be fostered, not only in science but in society, and in the life of each individual. This is the ultimate nature of the surge we are calling for.
////////////////////////////////////
• Humanity Inc. – from corporation to cooperation
• SECI-ASR (Self-Empowered Community Initiative for Augmented Social Resilience)
• New Dark Age
• Rage Inside The Machine
• Moral Capitalism: Why Fairness Won’t Make Us Poor
• The System – Who Rigged It?, How We Fix It
• The New Corporation – Why “Good” Corporations are Bad for Democracy
• The Tyranny of Merit – What’s Become of the Common Good?
• CHARGE (Cultural Heritage Asynchronous Research Grid Environment)
• Knowledge Negotiations
• Mathematical Courtesy
• Disagreement Management
• Collectigence
////////////////////////////////////
Chapter 1: REVOLUTIONS, THEORIES, AND CREATIVITY IN SCIENCE
[..]
Fragmentation and Change in Science (p.16)
Science is an attempt to understand the universe and humanity’s relationship to nature. How then is it possible for fragmentation to grow out of such an approach? The very notion of scientific understanding appears to be totally incompatible with a fragmentary attitude to reality. To understand how the fragmentary approach to the problems and difficulties discussed in the introduction came to pervade the whole of science, it is first necessary to understand not only what fragmentation means, but also how it operates in practice. this involves particularly subtle and complex issues. To begin with, it is important once again to distinguish fragmentation from simple specialization and from the practical division of knowledge into various subdivisions. Clearly some such form of specialization was the essential step in the development of civilization.
Indeed, the study of any field begins with a natural act of abstraction, in order to focus on certain features of interest. To be able to give attention to something, it is first necessary to abstract or isolate its main features from all the infinite, fluctuating complexity of its background.
When such an act of perceptive abstraction is free from an excessive mechanical rigidity, then it does not lead to fragmentation, but rather it reflects the ever-changing relationship of the object to its background. In order to recognize a face in a moving crowd, for example, an act of perceptive abstraction is required in which important features are isolated and integrated together. In a similar way, nonrigid focusing of the mind upon a field of interest will allow a corresponding integration of all relevant features in this field.
As a simple illustration, think of an intern who examines a patient in the emergency ward of a hospital. This doctor must make a preliminary diagnosis based on characteristic signs and symptoms that have to be abstracted from the infinite variety of appearances and behavior of the patient. This diagnosis therefore relies upon an essential division and classification of groups of symptoms and findings. But this division must never be fixed rigidly beforehand. Rather, the doctor must constantly check and confirm his or her hypotheses, changing them when they are not confirmed.
The preliminary diagnosis may point to some trauma in a localized region of the body, the dysfunction of an organ, a generalized infection, or some overall disorder of the metabolism. The recognition of a specific disease therefore depends upon the doctor’s ability to recognize a whole picture of symptoms which have been abstracted out of a complex background. Given this diagnosis, the intern will then call upon the assistance of a doctor who specializes in one of the subdivisions of medicine, for example injuries of the brain, disorders of the gastrointestinal system, fractures of the bones, infectious diseases.
When medicine works well, it combines this generalized knowledge with the more focused and detailed knowledge of the specialist. The danger, however, is always present that by converging upon a particular symptom, or area of the body, its connection with the larger whole of the patient’s lifestyle and the lifestyle of the whole society may be neglected. When this happens, the deeper nature of the disorder is obscured and specialization gives way to fragmentation, which will lead to inappropriate treatment.
In a similar way, science has developed into a number of general areas, such as physics, chemistry, and biology. In turn, each of these fields is further broken down into more specific specializations. Physics, for example, includes elementary particles, nuclear, atomic, molecular, condensed matter, fluids, astrophysics, and so on. Each articular discipline involves its own highly specific areas of knowledge together with characteristic theoretical and experimental approaches that have been built up through historical evolution.
In the seventeenth century, for example, the study of gases embraced both physics and chemistry, and a range of different approaches and experimental techniques were used in the one laboratory. The Irishman Robert Boyle, for example, was interested in the behavior of gases, both chemical and physical without distinction. In particular he became fascinated by what he called the “spring” of a gas, the way its volume changes with pressure. In order to make careful experiments of this relationship, it was necessary to isolate each particular gas from background contingencies, such as changes in temperature. But once Boyle’s law had been established, it became possible to widen the investigation and to explore the effect of both pressure and temperature on the same volume of gas. In turn, ever more refined experiments could detect deviations on the part of of individual gases, from this ideal behavior. But by now, the study of gases had divided itself into two main areas, their physical and their chemical behaviors, which were studied by scientists with quite different backgrounds and trainings.
The example of Boyle’s research illustrates two particular tendencies in specialization: first, that a topic of general interest, in this case the behavior of gases, can become divided into several distinct fields of study; and second, the way in which a scientific investigation proceeds by focusing, through carefully designed experiments, upon some particular property of a system and then attempting to study it in isolation from the wider context of its environment. Once this particular property is fully understood, the context can then be expanded to include additional effects and properties.
Ideally, areas of specialization are never rigidly fixed but evolve dynamically, in a state of flux, subdividing into narrow regions of specialization at one time then becoming more generalized at another. Provided that these boundaries remain fluid and scientists are aware of the wider context of each experiment and concept, then the problems of fragmentation need not arise.
[p. 19]:
As was suggested earlier, however, there appears to be no intrinsic reason why the movement between specialization and generalization, analysis and synthesis should of itself necessarily lead to fragmentation. Moreover, it is clear that individual scientists themselves would hardly make a conscious decision to carry out their research in a fragmentary way. How then has the present fragmentation of science come about? Clearly it must involve some particularly subtle factors that have by now become built into the very way that science is carried out.
Our proposal is that fragmentation does not so much arise from some defect in the scientific approach. Rather it has its origins in the general ways in which human beings perceive and act, not only as individuals but, more importantly, on an organized social level. As an example (which will be explored in more detail in the next chapter), fragmentation arises in scientific communication and this becomes embedded in the very way the languages of science are used. And since the causes of such fragmentation are in general mainly subliminal, they are extremely difficult to detect and correct.
[…]
Novelty and Conservation in Scientific Theories (p.25)
The ideas discussed in the previous section have something in common with those of Thomas Kuhn, the historian and philosopher of science whose The Structure of Scientific Revolutions aroused much attention in the 1960s. A closer examination, however, reveals subtle but significant differences between our ideas and those of Kuhn, particularly in connection with the nature of change and conservation in science. More specifically, we differ from Kuhn especially in the interpretation of the breaks that occur in the development of science and in our suggestions of ways in which these can be overcome.
On the basis of a study of the history of how scientific ideas develop, Thomas Kuhn argued that the prevailing activity of science takes place during long periods of what he called “normal science,” periods in which the fundamental concepts are not seriously questioned. This “normal science” then gives way to a “scientific revolution” in which theories and ideas change in radical ways as whole new systems of concepts and approaches are created. Kuhn calls these overall systems of concepts and approaches paradigms. Paradigms include not only systems of theories, principles, and doctrines, but also what we have called the “tacit infrastructure of ideas” which are transmitted by later generations of scientists in a kind of apprenticeship.
Kuhn argued that, following a scientific revolution, the new paradigm is “incommensurable” with what came before. This clearly suggests a break or fragmentation with the evolution of science. Kuhn’s term “incommensurable” is not too clear. It seems to imply that a new paradigm does not have enough to do with the old to permit even a common measure. Incommensurability, in this sense, is quite different from notions such as contradiction or incompatibility, which imply some common infrastructure with opposition lying only in certain points so that a measure of divergence or lack of agreement can be made. Kuhn’s term, however, implies that no such measure is possible. Perhaps it would have been better to say that two paradigms are mutually irrelevant. In this sense, those who understand one paradigm might, by a special effort, understand the other. But they would feel that this has little to do with what they regard as the basic framework in which truth is to be grasped. They would have little motive for paying serious attention to the alternative paradigm. Clearly, if Kuhn is correct, the new paradigm therefore leads to a very basic and serious form of fragmentation.
It is therefore important to question Kuhn’s whole analysis of this incommensurability and ask if such a fundamental dislocation of ideas must always accompany a scientific revolution. It is also necessary to go into Kuhn’s notion of “normal science.” In fact, Kuhn did not imply that this was a norm or ideal to which science should approach following a revolution. Rather he argued that this was the traditional way in which scientists have worked in the past.
In this book it will be argued that science need not, in fact, work in this way and that Kuhn’s “normal science” has no more force than that of custom and habit. A closer analysis will show that during periods of “normal science,” quite significant changes, in fact, take place and that true creativity cannot be bound or limited to periods of revolution alone.
But to return to this notion of a scientific revolution. The discussions of this chapter will show that the whole issue is far more subtle than that of opposing two incommensurable paradigms. Indeed there is a potential for a continuously creative approach in science so that any abrupt discontinuity of ideas is not inevitable.
As a preliminary example, let us look at one of the major scientific revolutions to take place before this century, a revolution in the understanding of the basic nature of motion. According to Aristotle, all bodies have their natural place in the universe. When a body has discovered its natural place, it will remain at rest unless acted upon by some external force. Aristotle’s theory corresponds to what could be called a “common sense” view of nature. No matter how hard a stone is thrown, experience shows that it eventually comes to rest on the ground. Similarly a cart comes to rest when the horse tires. “Common sense” suggests that all things eventually come to rest, and remain that way unless moved by some external force.
Newton‘s system, which replaced Aristotle’s, argued that the natural state is one of motion, in which rest, or zero velocity, happens to be a special case. An object therefore moves in a straight line, or remains at rest, indefinitely unless some force acts on it. Under the action of a force, the motion changes and the rate of change is expressed by Newton’s second law of motion. Newton’s laws of motion appear, at first sight, to contradict “common sense,” for they suggest that if all opposing forces are somehow removed, then the stone and the cart will continue to move in a straight line forever.
Clearly, the gap between Aristotelian and Newtonian concepts is extremely wide. In the Newtonian paradigm, for example, Aristotle’s notion of a natural place is completely beside the point, while in Aristotle’s system, there is no room to consider Newton’s idea of natural motion. The two ideas, therefore, appear to be unrelated to the point that one is not even relevant to the other. However, a closer examination of Newton’s “scientific revolution” shows that, in some areas, a sudden dislocation of concepts and ideas did not in fact take place. To begin with, part of the old tacit infrastructure of ideas was carried over into Newton’s scheme. Furthermore, other significant changes occurred in the longer period of “normal science” which followed. In fact, while a considerable confusion of the two sets of ideas and concepts existed for a long period following Newton, this did allow for the possibility of a dialogue between the two paradigms. In this sense the two paradigms were never absolutely incommensurable and indeed some form of creative dialogue could always have been held between them.
During the Middle Ages, people accepted Aristotle’s ideas as part of a tacit infrastructure of their worldview. Gradually, following Newton, another worldview arose in which Aristotle’s earlier ideas began to seem strange and beside the point. By the end of the eighteenth century, therefore, Aristotle’s notions on motion appeared to be quite incommensurable with Newton’s. Yet a closer examination shows that, in the Newtonian revolution, not everything had been swept away. For example, the notion of what constituted a material body, and what was the actual structure of space and time did not change in any radical way at least at first. The actual Newtonian revolution could best be described, therefore, as a radical change in certain ideas, set against a general background of concepts that remained unchanged.
Indeed the sense of mutual irrelevance of the two paradigms actually arose later, as the implication of Newton’s ideas were unfolded across the rest of physics. For as Newton’s ideas spread, they began to transform general concepts about the nature of matter that had not been closely examined in the initial “revolution.” For example, Newton’s laws of motion apply not only to apples and cannonballs but also to the moon and the planets. But clearly, if the same laws govern the heavens as they do bodies on earth, then there can be no essential difference between these two forms of matter.
In this way, one of Aristotle’s basic assumptions about the nature of the universe was denied. A similar change took place in the notion of cause, for the approaches of Galileo, Kepler, and Newton showed that the concepts of formal and final causes, advocated by Aristotle, were no longer needed in physics. Therefore, as the new ideas made their effects felt, they began to transform the whole framework of traditional modes of thought. As the old framework was gradually dropped and new notions of cause, motion, and matter evolved, science underwent a major transformation in the way it looked at the world, a change which was absorbed into the new tacit infrastructure.
Clearly, while major changes took place during the Newtonian revolution, the old and new infrastructure of ideas were not, initially, incommensurable on all points. However, in the period of “normal science” which followed, the older infrastructure was eroded and transformed by the many implications of the new ideas. In this way the implications of a “scientific revolution” can be far-reaching and will continue to manifest themselves during the period of “normal science” that follows.
With Einstein’s theory of relativity and the quantum theory, traditional concepts of motion, matter, and causality changed yet again. For example, the Newtonian concept of absolute space and time, a holdover from earlier Aristotelian notions, was finally found to be incompatible with Einstein’s relativistic ideas. In addition, the classical concept of a particle’s trajectory did not cohere with the notion of a continuous quantum transition.
In this and in many other ways, relativity and quantum theory continued the revolution that was started by Newton, and continued to transform the general tacit infrastructure of ideas that underlie physics. One particularly significant aspect of this change was to place a much greater reliance on mathematics. As was pointed out in the Introduction, the idea that mathematics expresses the essential reality of nature was first put explicitly, in modern times, by scientists, such as Sir James Jeans and Werner Heisenberg, but within a few decades, these ideas were being transmitted almost subliminally.
As a result, after passing through graduate school, most physicists have come to regard this attitude towards mathematics as being perfectly natural. However, in earlier generations such views would have been regarded as strange and perhaps even a little crazy – at all events irrelevant to a proper scientific view of reality. So yet again, while the scientific revolutions of this century are generally viewed as arising explicitly in the first three decades within quantum and relativity theories, in fact radical changes continued to take place in the post-revolutionary decades that followed. During this period of so-called “normal science,” the whole attitude toward the significance of mathematics began to change. Where it had once been regarded as an important tool for unfolding the implications of ideas, concepts, and models, now it was believed to contain the very essence of the scientific ideas themselves.
Creativity and Metaphors (p.30)
[…]
Hamilton-Jacobi Theory (p.39)
Fragmentation in science arises in several ways, in particular through the mind’s tendency to hang on to what is comfortable and secure in the subliminal infrastructure of its tacit ideas. In turn, this leads to a false perception of the radical nature of change during scientific revolutions, in which old and new paradigms are viewed as “incommensurable,” and to an underestimation of the degree of change that takes place during long periods of “normal” science. It is generally believed, for example, that following a major scientific revolution, scientists must consolidate their findings and unfold the new ideas in ways that are not necessarily as creative as in the revolution itself. However, a closer examination of the history of physics shows that a number of very powerful metaphors were developed during this period of “normal” science. Never pursued with sufficient energy and courage to initiate creative new discoveries, they were stifled by the weight of the whole tacit infrastructure of familiar and comfortable ideas that prevailed at the time.
During the nineteenth century, for example, there arose an alternative way of treating the mechanics of moving bodies, which at the time received too little attention. Newton had approached motion in terms of the definite paths of trajectories taken by particles. These trajectories were calculated using differential equations that were determined by the initial positions and velocities of the particles, and by external forces that acted at each point on the path to produce changes in the particle’s speed or direction.
The Hamilton-Jacobi theory, developed in the late 1860s, presented a new way of treating motion based on waves rather than on particles. In place of treating the motion of a particle as following a given path that is affected by external forces, the Hamilton-Jacobi theory is based upon a wave description in which all motion is perpendicular to a wave front. A simple image is given by the movement of a cork or a small piece of wood that is carried by waves on a lake. In this way the motion is determined by the waves as a whole, rather than by piecewise local actions of a force at each point in the trajectory of the particle.
Clearly, the Hamilton–Jacobi theory is radically different from Newton’s. Yet mathematicians were able to show that the two theories, in fact, generated the same numerical results. It was clear that these alternative theories contained essentially “incommensurable” ideas: that matter is in its essence of a particle nature, or that it is of a wave nature. Scientists, however, tended to concentrate upon the mathematical aspects of the new theory and to pay less attention to the curious situation that two apparently unrelated notions of the constitution of matter were able to cover the same range of experience and with the same results. In the light of the previous section, this situation suggests the possibility of making a metaphorical leap and saying, “A particle is a wave.”
Such a metaphor that connects the essence of the two theories would have, in a certain sense, anticipated the modern quantum-mechanical notion of wave-particle duality. That is, the same entity (e.g., an electron) behaves under one set of circumstances as a wave, and in another set of circumstances as a particle. A more detailed discussion and development of this metaphor could have led in the mid-nineteenth century to the general outlines of the modern quantum theory, almost without any further experimental clues at all.
Indeed, William Hamilton had already unfolded the essential similarity between particle and wave, which is implicit in this metaphor, by considering a ray of light. This is basically a form of waves and yet has a trajectory resembling that of a particle. The ray, however, still does not quite give a full account of the motion of a particle. To obtain this, it is necessary to consider a wave packet, which consists of a group of waves each having nearly the same wavelength. These waves will combine together within a small region of space to produce an intense disturbance, while outside this region their intensity is negligible. The wave packet therefore suggests a model of a particle that is based on the wave concept. This packet can be shown to move with what is called the group velocity and its motion can be calculated from the Hamilton-Jacobi equation.
When this is done, the theory yields both Einstein’s relationship, which shows that the energy of a “particle” (e.g., a light quantum) is proportional to its frequency, and de Broglie’s relation, that the particle’s momentum is inversely proportional to its wavelength. Both these relations, which are implicitly contained within the Hamilton-Jacobi theory, are in fact the key relationships in the foundations of quantum theory. Furthermore, by means of a small but natural modification to the Hamilton-Jacobi equation, it is possible to derive Schroedinger’s equation, the basic equation of the quantum theory.
Scientists in the nineteenth century could, therefore, have been led to most of the essential features of modern quantum theory, through the exploration of the metaphor that
“a particle is a wave.” All that would have been needed to complete the quantum theory would have been to fix certain numerical constants by means of experiment. (Specifically, the numerical constant that appears in de Broglie’s relationship. This is implicitly contained within the Hamilton-Jacobi theory and determines the actual value of a particle’s frequency and wavelength once a numerical proportionality constant is known. The value of this constant is calculated from a measurement of Planck’s constant.)
The essential point which can be learned from this example is that metaphors can sometimes have an extraordinary power, not only to extend the thought processes of science, but also to penetrate into as yet unknown domains of reality, which are in some sense implicit in the metaphor. While all metaphors may not be as powerful as that between the Newtonian and the Hamilton-Jacobi theories, it does suggest that scientific metaphors which link unrelated but fundamental concepts may be especially significant.
In the case of the Hamilton-Jacobi theory, however, scientists were mesmerized by the whole tacit infrastructure of Newtonian mechanics, which viewed motion always in terms of trajectories and particles. By clinging on to this underlying matrix of ideas, it became impossible to treat the wave theory of matter as a potential clue to new fields of reality. Instead the Newtonian theory, along with all its infrastructure of subliminal ideas about particles and trajectories, was believed to correspond to reality in an essential way and the Hamilton-Jacobi theory was treated as an artifact or simply a mathematical transformation of Newton’s equations that could be used to facilitate certain types of calculation. So, to the scientists of the nineteenth century, the Hamilton-Jacobi equations did not have any deeper meaning.
Indeed it was a century before scientists were able to seriously consider this new view of reality – a view which had in fact been implicitly contained in what was already known. This move required them to overcome the common presupposition, taken for granted over centuries, that nature is constituted only of bodies that are essentially similar to those of ordinary experience, but simply smaller. One of the major steps in changing this view was taken by Niels Bohr, who proposed, in the spirit of the metaphor, that electrons had discrete orbits that changed discontinuously. Most physicists, however, took this idea in a literal fashion, and for a time, scientific thinking involved an uneasy marriage of classical and quantum concepts. It was not until the radically new perceptions of de Broglie (1924), Heisenberg (1925), and Schroedinger (1926) that physics was able to produce a reasonably complete and consistent theory of the atom. However, if the wave nature of matter, implicit in the Hamilton-Jacobi theory, had been taken as more than a mere mathematical artifact, progress would have been much more rapid. Indeed, the general attitude of “normal” science among nineteenth-century physicists prevented a truly creative extension of classical mechanics and the anticipations of the basic features of the quantum theory.
The Hamilton-Jacobi theory actually contains a number of additional interesting and fruitful metaphors which could also have been explored in the nineteenth century. For example, the equations themselves can be mathematically transformed in a special way so that the actual order of motion they describe is not affected but the wave forms themselves change. In other words, one wave form can be transformed into another wave form without affecting the physical outcome of the motion. What is particularly significant about these “canonical transformations,” as they are called, is that in order to leave the actual motion unaffected, time and space must be treated on an equal footing. In other words, time and space become interchangeable, with a new time variable being defined not only in term of the old time variable but also in terms of the old space variables.
The canonical transformations, which are basic to the Hamilton-Jacobi equations, therefore suggest a metaphor in which time and space are, in a certain way, equated. The Hamilton-Jacobi theory therefore anticipates a key feature of both the special ad the general theories of relativity – that the laws of physics are unchanged (invariant) to transformations in which time as space are treated on an equal footing.
=====================
• Noether’s first theorem
=====================
Yet another metaphor can be extracted from the Hamilton-Jacobi theory by considering that these equations can be derived from what is called a variation principle. Newton’s approach to motion was based on the idea of a differential equation that describes the motion as a succession of steps in which each stage follows continuously from the preceding one in a fashion that is typical of mechanical systems. The variation principle, by contrast, starts not from a differential equation (in which the motion is analyzed into infinitesimal steps) but from an integral which depends upon the whole trajectory over a finite period of time. This integral is called a Lagrangian, and the variation principle approaches motion as if a particle were attempting to “minimize its Lagrangian.” The motion of a particle, in this approach, depends upon a whole period of time, rather than, as suggested by Newton, upon a succession of instantaneous mechanical reactions to an external force. The Hamilton-Jacobi theory is, therefore, determined by something that approaches teleology: it appears as if all motion is governed by the need to attain an “end.”
Put in the form of a metaphor: “Mechanism is teleology” (of a particular kind). This reverses, in a creative way the usual habit of thinking in which what appears to be teleology is understood by saying that it can ultimately be explained by, or reduced to, mechanism (of a particular kind). Indeed, if the full implications of this metaphor are unfolded, they could perhaps lead to fruitful new insights into the age-old question as to whether or not there is a teleology in nature and if so, what it means. In a similar fashion, the metaphor in which time and space are equated through the canonical transformations of the Hamilton-Jacobi theory could perhaps lead to deeper insights into the relationship between relativity and quantum theory – an area which at present contains a number of incommensurable features.
[…]
Similarities and Differences: Heisenberg’s and Schrödinger’s Approaches to the Quantum Theory (p.45)
The unfolding of a metaphor that equates different and even “incommensurable” concepts can, therefore, be a very fruitful source of insight. But the procedure is by no means straightforward. The first difficulty that is encountered is not only that dissimilar things must be equated but that this must be done in a way that is sensitive to their basic differences, implications, and extensions. Initially, of course, scientists may fail to recognize the essential similarity between different things, for this requires a creative act of perception. But once this perception has been achieved, science may then fail to see the essential differences that are also inherent within the metaphor. Clearly the problem with thought is that it often fails to be perceptibly sensitive to similarities and differences and instead applies mechanical habits of seeing similarities and differences.
In the examples given in this chapter it is clear that, in science, perception of similarities and differences takes place primarily through the mind (e.g., Newton’s perception of a certain basic similarity between the apple, the moon, and the earth), and much less through the senses. As science developed, this aspect of perception through the mind grew more and more important. Indeed, very little of what could be called direct sense perception takes place in physics today. At one time scientific instruments, such as the telescope and the microscope, could have been considered as direct extensions of the senses, but today, the connection between experimental apparatus and human experience is becoming increasingly remote. The realm of physics is now that of perception through the mind, and theory dominates over experiment in the development of the scientific perception of nature.
An example of the important role that theory plays in scientific perception, and which also shows how perception can fail to make a proper discrimination, is provided by Heisenberg‘s and Schrödinger‘s formulations of quantum theory. Initially these were two separate, and almost incommensurate, formalisms that described identical phenomena and could have formed the basis of a potential metaphor. The Heisenberg theory describes atoms in terms of mathematical objects called matrices. These matrices are arrays of numbers that obey well-defined rules of mathematical operation. In Heisenberg’s theory, the numbers in these arrays correspond to various observable quantities of the atomic system. While this theory was remarkably successful in accounting for various experimental results on the spectra of atoms (the patterns of light emitted when atoms are exited), it was not able to give a conceptual picture of the atom together with a satisfactory description of what the theory meant. However, within a matter of months after Heisenberg’s discovery, Schrödinger published his “wave function” approach, which not only gave correct numerical results but also generated an intuitive picture of the hydrogen atom, in terms of standing electron waves around a central, attractive core.
At first it appeared that Schrödinger’s theory would quickly supersede that of Heisenberg and that the latter’s theory had been a stopgap procedure on the way to formulating a more complete description of the atom. However, as it turned out, matters were not so straightforward. To begin with, when Schrödinger’s equation was extended from the hydrogen atom, with its single electron, to more complicated atomic systems, it became apparent that the wave function itself was by no means as intuitive as had been first supposed. Instead of being a wave in our three-dimensional space, the function existed in an abstract, multidimensional space, and pictures of electron waves around a nucleus proved to be something of an abstraction. But more important, physicists discovered that, under fairly general conditions, the two approaches, Schrödinger’s and Heisenberg’s, were mathematically equivalent.
This formal mathematical equivalence between the two theories was a powerful step but it soon led physicists to ignore the essential differences between the two formulations and to consider them as nothing but alternative methods for calculating results to particular quantum mechanical problems – Heisenberg’s approach proving advantageous in some instances and Schrödinger’s in others. However, closer analysis shows that the two theories are not completely equivalent – an observation which is generally neglected. It turns out that their mathematical equivalence is true only under certain tacit, rather than explicitly stated, assumptions. In fact, more detailed examination of the two approaches shows that they exhibit certain significant differences. In the Schrödinger approach, for example, the quantum system is described by a wave function, which is the solution to Schrödinger’s equation. Mathematically this wave function is a continuous function in space; in other words, the continuity of space-time is built into the whole Schrödinger theory. By contrast, Heisenberg’s theory is not committed to such continuity, for the physical properties of the quantum system do not come from a continuous wave function but from a matrix of discrete numbers.
If physicists had chosen to treat the Heisenberg and Schrödinger theories in a truly metaphoric fashion, then they may also have been able to unfold the implications of their various similarities and differences. Specifically, it would have been possible to explore the idea of space-time both in the context of discreteness and of continuity. In this way, a theory of space-time may evolve which is non-local and non-continuous at very small distances but, in the limit of larger scales, becomes continuous and local. By taking such a metaphorical relationship seriously, and remaining sensitive to both similarities and differences it may be possible to gain new insights from these two approaches to quantum theory.
[…]
Thought at Play (p.48)
[…]
The High Cost of Paradigms – An Alternative View of Science as Fundamentally Creative (p. 52)
[…]
Free Play and Popper’s Notion of Falsifiability (p. 58)
[…]
Summary and Outlook (p. 61)
[…]
=======================
• de Broglie – Bohm theory
=======================
///////
Chapter 2: SCIENCE AS CREATIVE PERCEPTION-COMMUNICATION (p. 63)
Is it possible for science to operate in a radically new way, in which fundamentally different ideas are considered together and new perceptions made between them? In the previous chapter it was shown that the essence of creativity lies in the ability to make such fresh perceptions and it was also hinted that communication plays a key role in such perceptions. In the case of Helen Keller, for example, her moment of insight, and the way in which it was unfolded, involved communication in a very important way. In this chapter the whole question of communication is explored in much greater detail and it is suggested that communication is essential for the creative act as is perception through the mind. Indeed, within this context, perception and communication are inseparably related, so that creation arises as much in the flow of ideas between people as in the understanding of the individual alone.
///////
Perception Through the Senses and through the Mind (p. 63)
Perception through the senses does not depend upon the immediate physiological details of the eyes or ears alone but on a much wider context that involves the whole disposition of the individual. In the case of vision this has been investigated from a number of different perspectives. Scientists have shown that seeing requires the active movement of both the body and the mind. Visual perception is therefore intentional and not a passive act.
[…]
Sense perception is therefore strongly determined by the overall disposition of both the mind and the body. But, in turn, this disposition is related in a significant way to the whole general culture and social structure. In a similar way, perception through the mind is also governed by these wider issues. A group of people walking through the forest, for example, see and respond to their environment in different ways. The lumberjack sees the forest as a source of wood, the artist as something to paint, the hunter as various forms of cover for game, and the hiker as a natural setting to explore. In each case the wood and the individual trees are perceived in very different ways which depend on the background and expectations of the walker. Clearly the manner in which an overall social disposition influences how things are seen has considerable importance for science. For, as was pointed out in the previous chapter, this mental perception is also linked to the creative act. Clearly the context of creativity extends into a much wider, social field.
It is important, at this stage, to be clear about the exact nature of perception in science. In the seventeenth and eighteenth centuries the human senses generally provided the major source of scientific information. However, by the nineteenth century they began to play a relatively secondary role. In their place, scientific instruments began to supply the primary data of science. During the seventeenth century, relatively simple instruments, such as the microscope and the telescope, could still, however, be regarded as extensions of the eye. But today scientific instruments have grown to such a complexity that observations are more and more remote from immediate sense perception.
But of even greater significance is the role of theories , which are now science’s major link with reality. Theories determine not only the design of scientific instruments but also the kinds of questions that are posed in the experiments themselves. Clearly, modern scientific instruments can no longer be regarded as simple extensions of the senses. Indeed, even the raw data that they yield are generally fed directly into computers in the form of numbers and digitized signals. In perceiving the external world by means of this computer-processed data, the senses play a particularly minor role when compared with that of thought.
Perception in modern science, particularly in physics, takes place essentially through the mind, and it is here that the inward intention and general disposition most strongly affect what is “seen.” For example, the simple intention to look, or the decision to use an object in a certain way, now becomes the intention to investigate the consequences of a theory or the disposition to use a certain apparatus.
An additional feature of this scientific perception is its essentially social nature. For without a firm intention shared among many scientists, the complex equipment needed to carry out a modern experiment would never be built and used. The very nature of modern science and its theories is that it gives rise to the design of large and expensive pieces of equipment which require the operation of large institutions. In turn, this predisposes scientists to see nature in a particular way, for it feeds back into their theories and hence into the design of new experiments.
For example, a vast investment on an international scale is currently being made in building and operating elementary particle accelerators. But this, almost subliminally, predisposes scientists to develop theories in terms of particles and to design additional experiments that will give answers in terms of particles again. The whole social structure of physics has the effect of confirming the particle hypothesis of matter. As a consequence, other possibilities become more difficult to investigate.
In stressing that perception in modern science occurs essentially through the mind, it must not be forgotten that this was always a vital component of science. The observational data obtained by Archimedes in his bath, for example, had little value in themselves. What was significant was their meaning as perceived through the mind in an act of creative imagination. The major change occurring in modern science, however, is that this mental perception is more pervasive than it was in earlier times and its social nature is far more dominant.
It should now be clear that all forms of perception – both through the senses and through the mind – involve a cyclic form of activity. Incoming information is apprehended by the mind and, in turn, produces an outgoing activity in which further scanning and information gathering take place in order to confirm, explore, and reinforce what has been seen. This new activity gathers additional information, which is again apprehended by the mind, leading to yet more outgoing activity. But this is very similar to what happens in science as well.
Knowledge of reality does not therefore lie in the subject, nor in the object, but in the dynamic flow between them. However, since reality itself is inexhaustible and never fully covered by knowledge, it could also be said to lie outside the subject, while at the same time including this overall cyclic activity.
CONT. p. 67.
[…]
Communication is Essential to Perception in Science (p. 67)
Science is essentially a public and social activity. Indeed it is difficult to imagine scientific research, in any real sense, that does not involve communication within the whole scientific community. In other words, communication plays an essential role within the very act of scientific perception. Scientists are disposed in their thinking by a general background, or tacit infrastructure, of ideas, concepts, and knowledge. In addition, they constantly engage in a form of internal dialogue with the whole structure of their particular discipline. In this dialogue a scientist raises questions and meets points of view which are attributed to other scientists and to his or her own past work. In addition to the internal dialogue, scientists are actively engaged in their daily work with a social exchange of ideas and opinions through discussions, lectures, conferences, and published papers. Motivations, questions, and attitudes arise out of these dialogues, so that all scientific research, in the end, arises out of the whole subcultural matrix of science.
When insight occurs, it emerges out of this overall structure of communication and must then be unfolded so that it obtains its full meaning within it. As a particular insight unfolds, the scientist discusses the new ideas with colleagues and eventually publishes them. In this way criticisms are met and new suggestions exchanged within the scientific community. This leads to transformation of the original perception. This process of general discussion is so pervasive today that it becomes difficult to say who was originally responsible for creating a particular new idea. As each scientist attends seminars, writes papers, and holds discussions with colleagues, new perceptions arise uninvited out of the totality of the social and cultural milieu. Indeed it can truly be said that each scientist contributes something of significance to this communal matrix in which every major scientific discovery has its ultimate ground.
In view of this continuing social flow of ideas, how is it possible for fragmentation to arise to the point where communication becomes seriously blocked? In the previous chapter t was shown how a person can become limited by an overall “infrastructure of ideas” which is held to rigidly and almost unconsciously: But now the danger arises that this structure of ideas not only applies at the individual level but us held by the scientific community as a whole, so that it eventually begins to limit creative acts of perception. It is therefore necessary to make a careful examination of the way communication takes place between scientists. This includes not only individual scientists themselves but the institutions in which research is carried out, and general attitudes that are fostered and encouraged within the scientific community. Indeed this analysis of communication must be ultimately extended to the whole structure of human relationships themselves. For example, fear and mistrust may be engendered by rigid lines of authority, lack of job security, and concerns over status and competition. All these factors conspire to starve that sense of mutual confidence, goodwill, and friendship that is so necessary for the free play and open exchange of ideas.
If science is to engage in a creative new surge, then all this must clearly change. Within this book it is suggested that scientists could engage in a kind of free play of thought, that is not restricted by unconsciously determined social pressures and the limitations inherent in particular paradigms. Such free play could be extended into the form of an open dialogue and exchange of ideas within the scientific community so that each scientist becomes more able to realize his or her creative potential. When the tacit infrastructure of thought is no longer held rigidly within the community, then it becomes possible to sustain creativity at a high level throughout the whole of science.
The creative potentialities of free communication are not particular to science alone. They were, for example, of crucial importance in the education of Helen Keller, and they can be clearly seen in the operation of the visual arts. Consider a painter who is engaged in making a portrait. A particularly naive view of painting would conclude that the artist is attempting to portray the sitter “as he or she actually is.” However, a moment’s reflection shows that other artists will portray the same subject in totally different ways. So where does this “artistic truth” lie? An equally naive suggestion is that the artist is primarily concerned with the truth of immediate, “naked” visual perceptions. Yet all sensory data are deeply influenced by a person’s background and disposition. In the case of the artist, this includes everything that has gone before in the history of art, as well as with the artist’s relationship to the subject.
Psychological experiments have established that visual perception is clearly conditioned by the circumstances i which that perception takes place, for example, the “meaning” of the scene and which questions are put to the viewer at the time. Clearly the artist is not immune to this process and the “artistic vision” arises out of an outward communication with a vast matrix of ideas of ideas, social predispositions, and so on. In addition, the artist is also very much concerned with “inward perception,” a vision through the mind that is not dissimilar to that experienced by the scientist. These inward perceptions are affected by everything that the painter holds important about the history of art. Indeed the final painting must take its place within an artistic matrix that stretches over space and time. Each painting is an aspect of the history of art and acts to transform and complement it. Manet’s “Olympia,” for example, owes much to Goya’s “The Naked Maja,” among other paintings, and, in turn, inspired Cézanne to paint “A Modern Olympia.” Throughout the history of art the individual artist’s engagement with other painters, sculptors, and poets, and indeed with the whole culture, is intimately tied to the perception and execution of a work.
As in art, so in science does creativity flow out of a free and open communication. Indeed it is not possible to consider any fundamental separation between the mind’s perceptions and communication; they are an indivisible whole. Although for the purpose of analysis, it is always possible to divide them into separate parts, in actuality they are two aspects of the same process, which could be indicated by the hyphenated term perception-communication. Clearly it is inadequate to think of the scientist as related to reality through individual activity alone. His or her social communication extends throughout the whole scientific community and beyond, for technology acts on the whole society and environment, and in turn, society determines the direction of science through its policies and financial support and in countless other ways. the significance of free and open perception-communication in the creative operation of science makes it of key importance to discover how communication can be blocked or broken and how fragmentation of the scientific endeavor results.
Paradigms and Specialization as Sources of Breaks in Communication (p.70)
[…]
Metaphors as Ways of Healing Breaks in Communication (p.72)
Failures in communication within and between the sciences have been shown to be far more subtle and complex than may have at first sight been suspected.
In particular, across the historical context of science, a serious gap in communication occurs between ideas and concepts that are considered to be, using Thomas Kuhn’s terms, incommensurable. We suggest, however, that none of these breaks is inevitable and, indeed, that they can be bridged through the creative use of a from of metaphorical thinking.
At a simple level, take, for example, the conflict between the ideas of matter as fundamentally discrete or continuous. Arguments along these lines go back to the ancient Greeks, and at first sight, the two points of view appear to be incommensurable. However, on closer investigation it would appear that any theory of the continuous nature of matter can in fact be based upon an opposing theory involving discrete matter that is so fine as to have never manifested its nature up to the present time. Conversely, any theory of the discontinuous structure of matter can be explained as arising through the localization and concentration of a continuous background.
These two approaches have in fact been explored during this century. Light, for example, which had been thought of as having a continuous nature, was shown to consist of discrete quanta whose size was so small as to have hidden their individual nature until relatively recently. Likewise Einstein proposed that the particulate nature of matter may be explicable as concentrations and knots in a fundamental, continuous field.
In this example, therefore, what at first sight appeared to be incommensurable views, with little communication between them, were, on deeper analysis, shown to have a deeper interconnection. In the previous chapter other metaphors were shown to apply between Newtonian and Hamilton-Jacobian theories of mechanics. A further example is provided by electromagnetic phenomena, which at one time were viewed through two quite separate theories, one dealing with magnetic manifestations and the other with electrical. This example also shows how deeply the theoretical framework affects what is perceived in science.
Eighteenth-century physics, for example, treated the various manifestations of electromagnetism through two different theories: the theory of magnetism and the theory of electricity. Because particular effects were treated by these different approaches, physicists were never in a position to observe various manifestations as aspects of the one underlying phenomenon. Rather they perceived two quite different classes of events, those arising from magnetic forces and those arising from electrical charges and currents, which were thus fragmented from each other. In a sense the unification of these two fragments of one whole was first made by J. C. Maxwell with his theory of the electromagnetic field, first formulated in the 1860s. However, it remained to Einstein and his special theory of relativity (1905) to show how a total symmetry can be achieved through the metaphor: electricity is magnetism and magnetism is electricity.
It is interesting to note that Einstein’s seminal paper on the special theory of relativity, On the Electrodynamics of Moving Bodies, begins with a consideration of two very different explanations of the one phenomenon – the relative motion of a magnet and an electrical conductor. In one case the magnet is considered to move past the conductor, a loop of wire connected to an electrical meter. Through the electrical field associated with the moving magnet, a current is induced in the wire – the net result is a deflection of the meter. In the second explanation, the electrical conductor is moved past the magnet, which is now at rest. No electrical field is produced in this case; rather the magnetic force on the charged particles (electrons) in the wire cause a current to flow and a deflection of the meter. Two quite different and apparently incompatible explanations are therefore produced for one and the same phenomenon: the flow of an electrical current when a magnet and a wire move relative to each other.
Through his perception that relative motion was the essential point, Einstein was led to see electrical and magnetic effects not as absolute and independent but rather as relative to the state of motion. In addition, they are dependent on each other, for an electrical field in one frame of motion is a magnetic field in another frame. What is involved is a kind of metaphor in which electricity and magnetism are equated. Einstein’s insight widened the possible range of communication within physics so that today electromagnetic phenomena are perceived in a very different light from what had earlier been the case.
Of course Einstein’s perception went beyond this particular case, for he was led to postulate that time is not an absolute. To achieve the new unity between electricity and magnetism, Einstein had to suppose that time, measured in the frame that moves relative to the laboratory (say, the magnet), is different from time measured in the stationary laboratory (say, the fixed wire). This laid the basis for a conceptual understanding of what is known as the Lorentz transformation, in which space and time are, in a certain sense, interchangeable.
What emerged from this insight was a new metaphor: time is space. Again two apparently incommensurable concepts were discovered to have a deeper unity, and perception-communication was extended in physics. Indeed Einstein’s was one of the most revolutionary steps ever taken in the history of science, which profoundly altered both the mode of communication and the mode of perception of physics.
///////
Language in Science (p.75)
The question of communication leads, in a natural way, to a discussion of the whole nature of language in science. Language is normally considered to be a means of communication, but closer analysis shows that it can also lead to particularly subtle, yet deeply significant, breaks in the ability to communicate various concepts between individuals.
The world’s languages are almost infinitely rich in their abilities to deal with subtle distinctions of sense and meaning, to the extent that many linguists would argue that whatever can be thought and experienced can be expressed in language. However, in their professional lives people also tend to use language in more specialized and restricted ways. Conversations between lawyers, doctors, or physicists abound in technical jargon, particular turns of phrase, and special usages of language. Indeed within each professional group a particular term will be immediately understood along with all its rich allusions.
Within science, for example, there are even specialized usages confined to fields, such as biology, psychology, chemistry, and physics, in which terms that are basic to one discipline will be irrelevant, different, or even unknown to the other. Such specialized usages of language can of course lead to difficulties in communicating between the disciplines. As a result of the rapidity of its changes, the language of science is constantly changing in subtle but often radical ways. Moreover, as will be shown in this chapter, major changes are not only confined to “scientific revolutions” but may accumulate as a result of the gradual changes that take place during periods of “normal science.”
Of course, as with all language use, most of the processes described above take place largely unconsciously and unobserved and reflect the overall infrastructure of ideas embraced subliminally by the scientific community. In this way when fundamental changes in concepts, and in the ways that ideas are actually used, occur, language becomes used in quite new ways while everyone continues to believe that “nothing has fundamentally changed.” The result is a serious form of fragmentation in which scientists continue to talk together but in ways that are increasingly at cross-purposes or even incoherent.
This becomes a particular problem in the more mathematical sciences, in which a lack of coherence can occur between the mathematical formalisms and the informal way they are discussed on a day-to-day basis. Indeed a radical change in the way language is used in physics came about as a result of the discoveries of quantum theory. Its implications are so significant that they are worth discussing at length in the next section.
[…]
Heisenberg’s Microscope Experiment (p.76)
[…]
The Bohr-Einstein Dialogues and the Breakdown of Communication in Physics (p.84)
The major issue of this chapter is the breakdown in communication within science, especially as it arises in connection with discontinuities between the formal and the informal languages used by scientists. A particularly significant example of this failure to communicate arose between Bohr and Einstein, which, in a symbolic sense, still prevails in physics today.
Bohr first met Einstein during a visit to Berlin in 1920, when the two men discussed the various philosophical issues that lay at the heart of physics. Following Heisenberg‘s discovery of the uncertainty principle in 1927, they met at the Fifth Solvay Conference to discuss the meaning of these new discoveries in quantum theory. Throughout the 1930s the two men were involved in a long series of exchanges on the way quantum theory should be interpreted. Bohr, for his part, had introduced new notions into the informal language, so that the meaning of scientific concepts such as momentum and position, was to be taken as ambiguous. In other words, the meaning of such concepts no longer corresponds in a well-defined way to reality. Einstein, however, believed that fundamental concepts should have, in principle, an unambiguous relationship to reality. This view was in harmony with the essential role that Einstein had assigned to the notion of a signal in special relativity. It was a matter of principle that no signal should be transmitted faster than light. But this could not be maintained if the notion of signal became ambiguous in meaning.
To put this in a different way, both Einstein and Bohr emphasized particular notions of meaning in the informal language of physics. But while, for Bohr, the meaning of fundamental concepts could be ambiguous, in Einstein’s view they had to be unambiguous. The two men engaged in a long series of discussions about these issues over the following years. However, in retrospect, it becomes clear that it was never possible to resolve the issues that stood between them because their different use of informal language implied conflicting notions about the nature of truth and reality and about what is an acceptable type of scientific theory. Bohr began to feel that Einstein had turned in a reactionary way against his own theory. Einstein, for his part, felt that Bohr had become caught in what he called a “tranquilizer philosophy” which avoided fundamental questions. Although the two men began as good friends, indeed Einstein said that he had initially felt a real love for Bohr, they eventually drifted apart after many years of fruitless argument and exchanges of challenge and response.
This breakdown between the two men is clearly shown in a story told by Hermann Weyl, who was at Princeton Institute for Advanced Studies at the same time as Bohr and Einstein. Weyl felt that it was unfortunate that the two med did not get together, so he arranged a party for this purpose. But at the event Bohr and his students congregated at one end of the room and Einstein and his at the other. Clearly the two men had nothing left to say to each other.
Weyl’s story shows the enormous power of informal language, which forms a significant part of the tacit infrastructure of science. It also hints at the actual way science is carried out. What is particularly important about this example is the earnest and sustained efforts to maintain contact on what Bohr and Einstein regarded as the key issues in physics. But their differences did not arise within the mathematical formalism itself, for Einstein agreed that the formalism of quantum theory is essentially correct. Yet, as the result of the different ways they were using the informal language, the two men became separated by an abyss.
This separation had particularly serious consequences in the development of relativity and quantum theory, for there is now no common, informal language that covers them both. As a result, both theories are regarded as fundamental, they exist in an uneasy union with no real way of unifying them. Even within the quantum theory itself there is a serious failure of communication between the various interpretations.
There is so little awareness of the unbridgeable differences between physicists today because sustained efforts to engage in dialogue have not been made with the kind of persistence shown by Bohr and Einstein. Today the general atmosphere is such that a physicist can do little more than state, and restate, a particular point of view. Various approaches are generally taken to be rivals, with each participant attempting to convince the others of the truth of a particular position, or at least that it deserves serious attention. Yet at the same time, there is a general tendency to regard the whole question of interpretation and the role of informal language as not being particularly important, and instead to focus upon the mathematics about which everyone agrees.
/////////////////////////////
[ Example of “overmathematisation”: Max Tegmark: Mathematical Universe Hypothesis. ]
/////////////////////////////
[…]
The Causal Interpretation of the Quantum Theory (p.87)
[…]
The Causal Interpretation (p.88)
[…]
Objections to the Causal Interpretation (p.97)
[…]
The Role of Interpretations in Physics (p.101)
[…]
Summary and Conclusions (p.103)
[…]
///////
Chapter 3: WHAT IS ORDER?
[…]
New Orders in Society (p.105)
[…]
Orders and Categories (p.111)
[…]
A Formal Representation of Order (p.116)
[…]
Constitutive and Descriptive Order (p.119)
[…]
Chaos, Randomness, and Infinite Order (p.121)
[…]
The Full Richness of the Spectrum of Order (p.128)
[…]
The Quantum Theories and “Hidden” Orders (p.134)
[…]
Order from Chaos and Chaos from Order – The Meaning of Entropy (p.137)
[…]
Structure (p.141)
[…]
Ratio or Reason (p.145)
The understanding of structure and its expression in thought and language takes place primarily through reason. The word reason is based on the Latin ratio. A little consideration shows that a kind of ratio is indeed a key feature of reason. The general form of ratio may be written as \, A:B \, as \, C:D , with the numerical ratio \, A/B = C/D \, being a special form of this. Such a ratio means that \, A \, is related to \, B \, as \, C \, is related to \, D .
/////////////////////////////////////
Eudoxus’ theory of proportions
The theory of proportions is credited to Eudoxus and is expounded in Book V of Euclid’s Elements. The purpose of the theory is to enable lengths (and other geometric quantities) to be treated as precisely as numbers, which only admit the use of rational numbers. The Greeks could not accept irrational numbers, but they accepted irrational geometric quantities such as the diagonal of the unit square. This is because geometric quantities clearly exist. For example, \, \sqrt 2 \, is the geometric diagonal of a unit square, which is real and whose existence is obvious.
To simplify the exposition of the theory, we first fix a length, and we call a length rational if it has a rational multiple of the fixed length.
Eudoxus’ idea was to say that a length \, λ \, is determined by those rational lengths less than it and those rational lengths greater than it. To be precise, by the definition, we say that \, λ_1 = λ_2 \, if the following holds:
(i) any rational whose length is \, < \, λ_1 \, is also \, < \, λ_2 , and
(ii) any rational whose length is \, < \, λ_2 \, is also \, < \, λ_1 .
Also, by definition, we say that \, λ_1 < λ_2 \, if there is a rational length \, > λ_1 \, but \, < λ_2 .
This definition uses the rationals to define irrational numbers. This process seemed to avoid using infinity, but actually it used an infinite process. Not only that, in fact, modern real number theory is based on the same idea.
Richard Dedekind: [ Dedekind cut ]
/////////////////////////////////////
However, two things can be related only if they are different. But in Latin, the root meaning of difference is “carrying apart.” To “relate” comes from the participle of “to refer,” which means to “carry back.” In this process two things are, at least in the mind, carried apart to difference and then carried back to similarity and relationship.
The order of the line that was introduced earlier can therefore be described by the ratio \, A:B \, as \, B:C \, as \, C:D , and so on. Further, since any ratio can be expressed by the symbol \, R , it is possible to relate ratios in a similar way, \, R_1:R_2 \, as \, R_2:R_3 \, and so on. Hence from a simple ratio, a relationship or relationships can be defined.
The full development of such a hierarchy of ratios or relationships, which occurs in all areas in which the mind is used, is essentially the power of rational thought or reason. Irrationality can then be taken as the failure of such ratios to cohere. Rationality is thus an order, and indeed it is the essential order of thought.
Ordinarily a test for rationality is made with the aid of logic (which is generally taken to be a set of formal rules that thought must satisfy if it is to be judged as rational). The common attitude to such formal logic is to regard it as a static set of norms, which stand entirely on its own. Moreover, formal logic is in fact only a limiting aspect of a much broader, overall movement of reason. In harmony with the general approach to science in earlier chapters, it can be said that in its origin, the broader movement of reason is basically a perceptive act and formal logic is a relatively fixed abstraction from this movement.
The German language illustrates this better than English does, because its word for reason is Vernunft, based on the verb vernehmen, which means to perceive, with the connotation of perceiving through the mind. This can be rendered into English as “intuitive reason” or “perceptive reason.” The corresponding word which, in some sense, covers formal logic would be Verstand, meaning in this context not “to understand,” in the sense of comprehension, but rather “to stand firm.”
Clearly it is necessary that thought should have the possibility of standing firm, if it is to function properly. But this “firm standing” musts find its appropriate place in the broader context of of the flowing movement of intuitive reason. It is only in this broader context that thought can become the vehicle of creative perception. Indeed, when there is free play of the mind, thought has its ultimate origin in such perception. It then unfolds in a natural way, through proposition, composition, supposition, and disposition. It is transformed into something fairly well defined and, as it were, crystallized.
Such crystallization of of reason, which is ruled by formal logic, is indeed absolutely indispensable if the proposals in which thought begins are to be tested properly for their rationality and for their coherence with the actual fact. Nevertheless, formal logic has to be ready to dissolve back into flowing reason, whenever a sustained contradiction or opposition develops in the application of its relatively fixed forms. In such a case the mind will be able to respond with creative intelligence, to perceive new orders and new categories that generally lie “between” the static and unrelated extremes presented by pure logic (for example, simple orders of low degree and chaotic orders of infinite degree).
The above is a description of the proper order of rational thought. If, however, the mind is too rigidly attached to fixed categories and orders, then, as has already been seen through many examples, the free play needed for such a rational order becomes impossible. Instead the mind is caught up in false play, from which a creative response may be impossible.
However, it should be added that, as suggested in Chapter 1, the false play can take many subtle forms that are difficult to detect. One form is to see truth as absolutely identified with formal logic. But another is, similarly, to identify truth with intuition and to fail to be open to the need for rigorous tests of this intuition, under appropriate circumstances, with the aid of formal logic. Moreover, rigidly fixed opinions, which are actually based on the misuse of formal logic, often present themselves in a somewhat vague and undefined guise that pretends to be genuine intuitive perception. This is especially common in the case of prejudices, that is, pre-judgements. They are evidently of a basically intellectual character but are nevertheless generally experienced in a deceptive way as intuitive perceptions and feelings. It follows then that the proper function of reason requires a creative intelligence that is free of every kind of excessive fixing of though, in whatever form this may appear.
Mathematics is an especially significant example of the interweaving of intuitive reason and formal logic in the kind of process that has been described above.
In this connection, it is interesting to note that the mathematician John von Neumann defined mathematics as “the relationship of relationships.” Evidently this implies an indefinitely extended structure of thought, formed in a process in which relationships of one kind are interwoven with relationships of other kinds, while this whole is organized by relationships of yet different kinds, and so on without limit.
/////////////////////////////////
/////////////////////////////////
The really creative act of a mathematician is to perceive the germ of this vast structure of relationships, and to unfold it into an ever more developed structure of thought that is constantly tested for cohererence against the rules of formal logic.
It is clear from the above discussion that ratio or reason is the essence of mathematical structure. But such ratio can be discovered in all areas of life. Thus, a person can find a complex structure of ratio in his or her experience of nature: for example, in the flowering movement of perception of the ever-changing orders to be observed in the wood, as was discussed earlier.
Similarly, there are such structures of ratio in a house, a crystal, the panorama observed from a high mountain, a human body, a painting, the use of language, and society itself. Such ratio is grasped intuitively as well as through the intellect. Its field is not exhausted through sense perception alone, for it also applies to the inward perception of feelings. Thus a person may say of an emotion that it is, or is not, in proportion to the situation that generates it.
Indeed whatever we apprehend is apprehended through some form of ratio. For example, to recognize anything whatsoever is to see that as various ratios are related to the object, so are they related to our mental concept of it. This is of course just what is also done in mathematics and in its applications.
Mathematics, however, has the advantage of being able to discuss pure ratio (for example ratios of ratio) without requiring a specified substratum lying in some object or sensory experience. In some areas this ratio may be so clearly defined that it permits an unfoldment of long chains of inference, whereas in other areas these chains are relatively short. But, as indicated in the Introduction, this is done at the expense of going to high levels of abstraction.
A key form of ratio is analogy, which is, according to the dictionary, a kind of proportion. As thought develops form the initial flash of creative perception, the ratio in it unfolds and articulates and so develops into a structure, in the way that was earlier described. This kind of structure is essentially an analogy to whatever the though is about.
If the analogy is good, the “propositions” in the ratios of the thought are similar to those within the object of thought; otherwise it is a poor analogy. This leads to the suggestion that thought moves naturally toward the improvement of analogy.
The notion proposed above brings us back once again to Korzybski‘s statement that whatever we say anything is, it isn’t. For after all, no analogy is equivalent to the object itself. Every analogy is limited. And if what we say is an analogy, then the object cannot be what we say it is. However, the essential proportions or ratios in both may be similar, but there is always room for newer and better analogies.
========================
[ The evolutionary development away from describing “what something is” toward describing “how it behaves.” ]
========================
To test the success of such analogies involves the cycle of activity that was discussed in earlier chapters. Each thought, with its content of analogy, gives rise to a disposition to act, which contains within it a set of proportions or ratios similar to those in the thought. The action is therefore imbued with a similar ratio or reason.
The fact that objects so generally respond in harmony to such action suggests that everything must likewise contain something at least basically similar to ratio, and that is what makes it possible for the world to be intelligible to human beings. Thus, intelligence, which includes creative perception of ratio, and intelligibility are not two separate and unrelated qualities, but rather are inseparable aspects of a single overall reality.
The fact that there is such an intimate relationship between human intelligence and the intelligibility of the universe can be understood in terms of a notion, commonly held during the Middle Ages, that each person is a microcosm, and thus stands as an analogy to the whole cosmos. This would explain how such a person could, through intelligent perception of ratio, produce analogies to whatever exists in the universe and even to the universe itself. For if this person already is an analogy to all this, then looking outward and looking inward will be two sides of one cycle of activity in which any aspect of the totality can in principle be revealed.,
///////
Thoughts and behavior patterns
///////
Model as perceived – Change as intended
///////
Mental models – Ingrained behavior
///////
[ Hom-O-Sapiens = Hom(Universe, Mind) ]
===========================================
[Mathematics is the study of all structures
that the human mind is able to perceive.
========================================
[Sense = Universe/Nonsense]
//////////////////////// Quotes from Poincaré:
Since half a century we have seen arise a crowd of bizarre functions which seem to try to resemble as little as possible the honest functions which serve some purpose….Nay more, from the logical point of view, it is these strange functions which are the most general….to-day they are invented expressly to put at fault the reasonings of our fathers….
— Henri Poincaré (1913)
Point set topology is a disease from which the human race will soon recover
Featured in: Henri Poincaré Quotes
///////////////////////
Consciousness is the projection Hom(Universe, Mind)
///////
Abductive pseudo-inverse
///////
Embedding Newton and restricting Einstein
///////
The cactus is a multidimensional plant
/////////////////
[…]
Summary (p.149)
The basic theme of this chapter is the proposal that order pervades all aspects of life and that it may be comprehended as similar differences and different similarities. An essential distinction was introduced between constitutive order and descriptive order, while at the same time it was noted that any actual order lies in a kind of spectrum between these limits. Order is therefore neither solely in the subject nor solely in the object, but instead in the cycle of activity that includes both.
Orders of varying degrees were then explored, leading to those of infinite degree and including all sorts of very subtle orders, such as those in language and in music. order in general was seen to lie in a spectrum between simple orders of low degree and chaotic orders of infinite degree of which randomness is a limiting case. Indeed there is no place in all this for the concept of disorder but only for random orders of infinite degree that are free from significant correlations and suborders of low degree. In this fashion, it is possible to discuss not only the emergence of orders of low degree out of chaos, as treated by Prigogine, but also the inverse process of the transformation of orders of low degree into chaos. This enables entropy to be considered as a particular feature of the general order of movement.
Structure was treated as an inherently dynamic notion, which includes not only the order of whatever elements are abstracted in thought, but also an arrangement, connection, and organization of these elements. Each structure was considered to be stabilized as the result of the mobility of whatever are regarded as its elements. the chapter concluded with a discussion of how structure is comprehended through a hierarchy of ratio, which may be apprehended in a perceptive act of intuitive reason.
Chapter 4: THE GENERATIVE ORDER AND THE IMPLICATE ORDER
Up to now, order has been considered as arising, basically, through a sequence of successions. This is indeed a very common form of order and perhaps the one that is most familiar. In this chapter, however, another kind of order, called the generative order, is introduced. This order is primarily concerned not with the outward side of development, and evolution in a sequence of successions, but with a deeper and more inward order out of which the manifest form of things can emerge creatively. Indeed, this order is fundamentally relevant in nature and in consciousness. In the following chapters its relevance to society will also be discussed.
The generative order will be explored with the help of a number of examples drawn from mathematics, physics, and the fields of art and literature. This will lead, in turn, to the implicate order, which is a particular kind of generative order that has been most fully worked out in physics. However, the implicate order will be found to have a broader significance, not only in physics but also in biology, consciousness, and the overall order of society and each human being.
Although specific proposals for how the generative order may be used will be discussed, it is not the main purpose, in introducing this new notion of order, simply to pursue its application in detail. Rather, it is to use these ideas in order to go more deeply into the meaning of creativity. In succeeding chapters, these notions will provide a base from which to move yet further in the general direction of creativity.
Fractal Order (p.152)
[…]
Generative Order (p. 157)
Mandelbrot‘s fractals are only one example of a generative order (in the fractal case, a generation which proceeds by repeated application of a simple shape but on a decreasing scale). Many other generative orders could be constructed in mathematics. However, the whole idea of generative order is not restricted simply to mathematics but is of potential relevance to all areas of experience.
Generative order can, for example, be seen in the work of a painter. Indeed, in a certain restricted sense the generation of form using Mandelbrot’s fractals can be compared with the various stages of painting. At least until this century an artist did not generally begin to work with detail but, in the case of a portrait for example, attempted to capture the overall form and gesture of the sitter with an initial sketch on the canvas. Such a painter may have even employed the trick of squinting at the sitter in order to cut down detail and emphasize tone and shadow. Gradually this initial sketch was built up and made more detailed, solidity being indicated by modeling, as the first layer of paint was added. As the painting progressed, detail was created in a progressive way, each time by building on the whole. Just as the complex forms of nature appear to be generated through successive additions of smaller and smaller detail, so at one level, a painting could be thought of as growing in a similar fashion.
But of course the generative order of a work of art is far more complex than the preceding description might suggest. For many orders of growth are involved which, in a great painting, are united within a single more comprehensive generative order. The painter may begin with a general idea, a feeling that contains, in a tacit or enfolded way, the whole essence of the final work. The next stage may be to observe the general scene and make sketches that rely upon the sense of visual perception. But in addition to the outward perception, there is also an inner perception in operation which is inseparable from the painter’s whole life, training, knowledge, and response to the history of painting. The outward and inward perceptions are, in turn, inseparable from an emotional and intellectual relationship to the theme and even to its literary and social values. Yet this vision is by no means rigid and fixed, for as the painter begins to work on the canvas, a new interaction takes place. He or she is constantly faced with both physical limitations and new potentials, in the very muscular activity of painting and in fresh perceptions of the growing painting beneath the brush.
In all this activity, what is crucial is that in some sense the artist is always working from the generative source of the idea and allowing the work to unfold into ever more definite forms. In this regard his or her thought is similar to that which is proper to science. It proceeds from an origin in free play which then unfolds into ever more crystallized forms. In science as in art it is necessary that what is done with more definite forms should continue at each stage to be open to the kind of free play that is essential to creativity. This holds even if, as with certain artists, such as Matisse, the ultimate form may be a simplification and generalization of what the artist started with, rather than an articulation of greater detail. Matisse’s initial creative perception was the constant guide to his activity. This can be seen in the large numbers of sketches and studies that he made for each of his final paintings, prints, and drawings. His generative idea was clearly the motivation for a subtle and meaningful simplification of lines and forms.
While the essence of the generative order of a painting ultimately escapes definition, it is clear that this order is very different from that of a machine, in which the whole is built out of the parts (i.e., in which the whole emerges through accumulation of detail). By contrast, one of the most important activities during the creation of a work of art is its unfolding, within a particular medium from the original perception. Something similar can be seen in music. Each composition is played in sequential, temporal order, yet its generation can never take place completely within such a sequential way. For that matter the unfolding of the meaning of the music in the mind of a perceptive listener is never totally sequential. This is especially clear in the work of Mozart, who is said to have seen a whole composition in a flash and then to have unfolded it by playing it or rapidly writing it down. Beethoven, by contrast, does not appear to have conceived of his works directly as a whole in precisely this fashion, for his notebooks contain themes and sketches worked over long periods of time. Nevertheless, the basic activity in Beethoven’s creative work is clearly still a constant unfoldment from a general notion of order.
Bach, for his part, appears to have comprehended fairly directly and as a whole the potential contained within a theme a few bars long, as the following story, told by his son Wilhelm Friedemann Bach indicates:
After he had gone on for some time, he asked the King to give him a subject for a Fugue, in order to execute it immediately without any preparation. The King admired the learned manner in which his subject was thus executed extempore; and, probably to see how far such art could be carried, expressed a wish to hear a Fugue in six Obligato Parts. But as it is not every subject that is fit for such full harmony, Bach chose one himself, and immediately executed it to the astonishment of all present in the same magnificent and learned manner as he had done that of the King.
But on returning to Leipzig, Bach was to accept the King’s challenge and compose a six-part fugue, nine canons, and a trio sonata on the Royal Theme which he submitted, along with his original fugue, as a Musical Offering. Clearly, in some implicit way the potential of Bach’s magnificent composition was perceived by him as enfolded within the King’s theme.
There is evidence that in speech the whole meaning is similarly generated quite quickly, along with the language needed to express it, which comes out as a sequence of words. What is said at any given moment, for example, has never been said exactly the same way before. In this sense the generative order of language is creative and bears a relationship to artistic and musical creation.
A major feature of a generative order is that through it a process of creation may begin from some broad encompassing overall perception. There is a clue from our language, for the word generative has the same root as general and genus. This supports the earlier claim that, in the arts, creative generation is basically from some general perception, which is then unfolded into particular forms. These may move toward greater and greater detail or, as in the case with Matisse, toward an expression of the general.
Fourier Analysis (p.160)
[…]
Goethe’s Urpflanze (p.162)
The simple example of Fourier Series demonstrates how a local order may basically follow from a global order, a reversal of the normal point of view in which global order is regarded as the outcome of local order. But as pointed out earlier, generative orders, especially of a global nature, have some far not been used extensively in science. It is interesting to note, however, that Wolfgang Goethe seriously investigated such a notion two centuries ago. In considering the relationships between the many varieties of plants there are in the world, and the variations that exist within a particular family and genus, Goethe was led to the notion of the Urpflanze. Literally this means an original plant and may, at first sight, appear to anticipate Darwin, who envisioned the proliferation of forms as arising through the evolution of original plants and animals. Goethe, however, was not referring to a particular physical manifestation of an original plant but rather to a generative principle or movement from which all plants of a particular kind emerged. There could, therefor, be no actual concrete example of an Urpflanze.
Goethe’s idea was that this generative principle is subject to a series of transformations of form, a dynamic movement as it were, and that the actual physical manifestation are plants of different but related shapes and features. For example, Goethe considered plants within a particular genus and arranged them as shown in the figure. The various forms of this plant are all related by similar differences. Therefore, the generative principle which, according to Goethe, gives rise to the whole set of plants contains an order of forms implicit within it. Such an ordered set of forms related by similar differences can also be obtained, for example, from a fractal generative process, if a series of small changes in the parameters determining the basic fractal order are made.
Because most of the prevailing ideas concerning the development of form were, at that time, expressed in terms of Euclidean geometry and sequential order, Goethe’s notion found little resonance in the science of the day. Nevertheless, perhaps with the development of new ways of looking at such questions, the time has come to explore such directions more fruitfully.
It would seem reasonable, and probably Goethe would have agreed, to suppose that the particular generative order described above is part of a still higher generative order of a wider range of species of plant, going on ultimately to the generative order of plants as a whole and even perhaps of life as a whole. In this way, the generation and evolution of life are thought of as more like the work of an artist than of an engineer. Moreover, considerations of this nature involve a fundamental change in the whole notion of what is meant by a hierarchy of orders. At present the word hierarchy, whose root meaning is a government by priests, contains the tacit idea that lower parts of a hierarchy are dominated by higher ones. But in the spirit of generative orders it is possible to consider hierarchies in quite a different sense. Moreover, the inclusiveness of orders, one within the other, is no longer a mere abstract subsumption in the sense that a more general category contains its particulars. Rather, the general is now seen to be present concretely, as the activity of the generative principle within the generative order. This suggests a new notion of hierarchy, in which the more general principle is immanent, that is, actively pervading and indwelling, not only in the less general, but ultimately in reality as a whole. Emerging in this fashion, hierarchies are no longer fixed and rigid structures, involving domination of lower levels by the higher. Rather, they develop out of an immanent generative principle, from the more general to the less general.
[…]
Orders in Art (p.164)
The nature of this dynamical hierarchy of orders, and the generative order that gives rise to it, can also be seen within paintings and musical compositions, and in our relationship to them. For the sake of simplicity, consider a drawing which is composed of lines of varying lengths, shape, and density made on a piece of paper. At one level the drawing can be apprehended as a series of marks, without any attempt being made to understand or interpret their meaning. The viewer becomes aware of the various orders that are created within this pattern as a whole, their rhythms and movement. The marks contain the potential for pattern, repetition, and imitation; that is, for an order of differences and similarities that appear as the eye moves across the field of the paper. In addition, variations and internal differences in their internal structure are also important. Their speed, changing thickness, and means of attack on the paper itself can give rise to complex emotional and aesthetic responses: to feelings of tension, sadness, energy, beauty, and so on. Clearly at the surface level of the marks themselves, with their symmetries and patterns, many orders are involved, with each individual line participating in several different orders and, in the context of each order, bearing different relationships with its neighbors.
But the surface order of the lines is only one aspect of a drawing, for it is representational, each line has a particular meaning that can be interpreted as being, for example, part of a body, foliage, a building, or as helping to indicate the solidity of a form or the effects of light. In addition, the relationships between the lines enable the artist to convey a sense of three-dimensional space on a flat surface. Therefore, as well as the complex orders of the surface itself there are a host of additional orders that involve the representation of space, movement, and solid objects. Again, each individual line participates in many different orders, each qualifying and complementing the others in subtle and complex ways. When all these orders are integrated through a comprehensive generative order, a great work of art results, but where integration is only partial or fragmentary then a mediocre work results.
What is particularly interesting about responding to a drawing or painting is the way in which the viewer interprets, decodes, and responds to this complexity of orders. For in different historical periods and in different cultures, marks and interpretations are made in different ways. The art critic Ernest Gombrich refers to what he calls schema, an idea not too dissimilar to Kuhn‘s paradigms, which takes the form of tacitly accepted conventions employed in the construction and viewing of a work of art. Within a given period, most artists employ particular schema, which are then absorbed unconsciously by the viewing public, who interpret the meaning of their works. When a school of art changes, the particular schemata are also transformed and the public may, at first consider the new work to be ugly, meaningless, or “wrong.” Until the new schema have been absorbed, the public are unable to interpret, and integrate with their inner perceptions, the work that stands before them. In one sense, therefore, an appropriate syntax has to be employed in reading the painting, just as a syntax is required to read and understand a novel or other piece of writing. In Chapter 3 a similar response was discussed with regard to music.
Just as a paradigm is realized when scientists develop fixed habits of mind that leave them insensitive to subtle changes and overemphasize certain obvious differences, so in a similar way can the artist and the viewer become rigid in their responses. Generally it is believed that some “genius” must come along and develop new ways of painting which then enable the public to “see” in exiting new ways.
A drawing or a painting contains many orders that operate together in a dynamical fashion as the work is being made and, for that matter, as it is being viewed. A particularly important aspect of this order is based on the notion of geometry used in its composition. Classical paintings can often be analyzed in terms of simple geometric forms, such as intersecting lines, triangles, rectangles, and circles, that are balanced and arranged in a harmonious fashion. Gestures made with the arms and glances of the eyes, if continued across the painting, will be found to make up one side of a geometric figure which is completed by other gesture lines or a spear, thigh, tree, cloak, or pillar. In addition, the invention of perspective by the architect Brunelleschi gave to painters, beginning with Masaccio, the possibility of a linear order generated by receding lines and planes of buildings and even of the human body. In a sense this underlying order, which gives structure to many Renaissance paintings, is similar to what we have called the Cartesian order: that is, the underlying use of a grid to portray space and, in the case of a painting, the tacit backdrop on which buildings, people, boats, rivers, and roads are ordered. It is not beyond the bounds of plausibility to see something of a Newtonian order also being anticipated in these Renaissance paintings.
On the other hand, the overwhelming passion of J. W. Turner, both in his paintings and poetry was the power of light and the movement of water, so that the underlying order of his art became a form of swirling motion or gyre. In addition, by borrowing from and going far beyond Goethe’s theory of advancing and receding colors, Turner was able to give the impression of a constantly rotating vortex within his paintings, a vortex of light, or of the violent motion of air and water that dissolves linear forms.
While Turner’s paintings are, of course, important for several reasons, one particularly striking aspect is the way in which the painter was able to overcome the old orders of geometrical structure through the power of his new vortex-like order of light, air, and water in constant motion. It is curious to note that these paintings were made some three decades before J. C. Maxwell published his electromagnetic theory of light, which replaced the Newtonian order of linear trajectories and rigid forms with fields in constant motion and internal rotation. In Turner’s “Regulus,” reproduced here, it is almost possible to see a new order of movement in which light and air replace the old rigid, linear structure. According to legend, the Roman general Regulus was blinded by the Carthaginians, who cut off his eyelids and forced him to stare at the sun. Turner’s painting is created from the perspective of Regulus himself. Around the general is a geometrical order of ships and buildings which are in the process of being dissolved by the blinding sun, whose light radiates from the center of the canvas to cover sea, ships, sky, buildings, and people alike. The painting seems, therefore, to symbolize a movement toward a new order in art that at least tacitly and implicitly aims to replace the old.
French generative orders, with their hierarchies of line, form, movement, and color require the viewer to respond in new and creative ways that are, for this reason, disturbing. The first attempts the Impressionists made to exhibit their paintings were met with considerable ridicule and critical attack. For in place of the traditional orders and schema of nineteenth-century French painting, Monet had begun to use spots of primary color in an attempt to express his perception of nature through a new way of re-creating on the canvas, a sense of the order of space. Thus, if you stand close to such a painting, you become aware of the pattern and strength of the color and of its apparent lack of representational form, but as you step back, a whole world with its three-dimensional order seems to come into being. For the viewers of nineteenth-century Paris, however, this use of a new generative order was so different from everything that had gone before in art that it proved to be, initially at least, totally unacceptable to most viewers.
This sort of thing has also happened with scientific revolutions (e.g., relativity). However, just as with scientific revolutions, it turned out that the degree of change had been overestimated, and that the Impressionists had really preserved much of what went before, while making subtle changes in what appeared similar. Corot and Rousseau had also painted in the open air, Constable had loaded his brush with pure white, Delacroix had placed spots of primary color one against the other, and Turner had anticipated Monet’s discovery that light dissolves form. So during this whole earlier period, which might have been called one of “normal art,” by analogy with “normal science,” a succession of fundamental changes was already taking place. With Monet, however, the change was finally so great that it had to be acknowledged that something really different had happened, and suddenly people began to feel that they were in the midst of a “revolution in art.”
[…]
The Implicate or Enfolded Order (p.172)
In science as in art, it is necessary to allow for the emergence, in creative perception, of new generative orders, which go beyond the individual content and involve the whole, common cultural experience. It is our suggestion that this implicate or enfolded order has such a potentiality. This form of order, which has been treated by David Bohm in Wholeness and the Implicate Order, is in a close relationship to that of fractals in the sense that, in both, there is a kind of whole generated from certain basic principles. Nevertheless, the implicate order extends the notion of generative order beyond what can be done with fractals. For this reason a detailed discussion of this form of order is given in this section. It will provide a powerful tool for exploring the ideas of creativity and generative order later on in this book.
The implicate order can be illustrated with the aid of the following device: Consider two concentric glass cylinders, the inner one fixed and the outer capable of being slowly rotated. The space between the cylinders is filled with a viscous liquid such as glycerin. When the outer cylinder is turned, fluid close to the inner, stationary, cylinder is held nearly at rest. Hence fluid in different regions of the space moves at different rates, and in this way, any small element of the glycerin is eventually drawn out into a long thin thread. If a drop of indissoluble ink is placed in the liquid, then it becomes possible to follow the movement of the small element by watching how the drop is drawn out into a thread until eventually it becomes so fine as to be invisible.
At first sight one may be tempted to say that the ink drop has been totally mixed into the glycerin so that its initial order has been lost and is now random or chaotic. But suppose that the outer cylinder is now rotated in the reverse direction: If the fluid is very viscous, like glycerin, and the cylinder is not rotated too quickly, then the fluid element will in fact retrace its steps exactly. Eventually the element will return to its original form and the droplet of ink will appear as if from nothing. (Such devices have in fact been constructed and the effect is indeed quite dramatic.) Clearly, what was taken for a chaotic and random loss of order was in fact a hidden order of high degree that was generated out of the initial simple order of the drop by turning the cylinder. Likewise this hidden order was transformed back into the original simple order of the drop when the turning of the cylinder was reversed. Clearly, there is a correspondence between this hidden order and the discussion in the previous chapter of how hidden order may quite generally be contained in what seems to be chance or randomness.
While the drop is present in hidden form, it may be said to be enfolded into the glycerin rather as an egg may be said to be folded into a cake: When the cylinders rotate in the reverse direction, the droplet then unfolds. With the egg in the cake, this is of course not possible, the reason being that the fluids in the cake are not sufficiently viscous.
To obtain an enfolded or implicate order from such hidden orders it is, however, necessary to consider a whole series of ink drops, enfolded in succession. Let us put in the first drop and rotate the cylinder n times. A second drop is now added and likewise enfolded n times, which also has the net effect of enfolding the first drop 2n times. A third drop is added and enfolded n times, the second being enfolded 2n times and the first 3n times. The process is repeated until many droplets have been enfolded. When the rotation of the cylinder is reversed, one droplet after another will emerge into an unfolded or explicate form and then fold back into the glycerin again. If this is done rapidly, the overall effect will be of a droplet which appears to subsist for a time within the moving liquid.
The experiment can now be extended so that the droplets are added in successively different positions. When the cylinder is reversed, the droplets will unfold in a line that moves across space. If the movement is rapid enough, this will give the impression of a particle that crosses space along a trajectory. However, this particle is simply a manifestation of a much greater enfolded or implicate order within the whole of the glycerin, most of which is hidden. As has been explained in Wholeness and the Implicate Order, this provides a good analogy to many of the basic quantum properties of particles, such as electrons. For example, the ink droplets may be so arranged that they produce a continuous track up to a certain point which then jumps discontinuously to start another track at a finite distance away, thus providing a way of understanding discontinuous “jumps” of the electron from one quantum state to another.
The above example helps to indicate what is meant by the implicate or enfolded order. What is essential to such an order is the simultaneous presence of a sequence of many degrees of enfoldment, with similar differences between them, for example, the ink droplets in the glycerin. Such an order cannot be made explicit as a whole, but can be manifested only in the emergence of successive degrees of unfoldment. This may be contrasted with an explicate or unfolded order, in which the similar differences are all present together, in a manifest and extended form. This explicate order is of course commonly found in ordinary experience and in classical physics.
It is clear that the explicate order corresponds very well to a worldview in which the basic notion is one of separate objects moving on trajectories. These trajectories, in turn, can be described in terms of Cartesian coordinates, as was indicated in Chapter 3. Although physics has gone through a revolution in which the notions of particle and trajectory have ceased to be basic, the underlying Cartesian coordinates still pervade the mathematical formalism. And thus, the mathematics has hidden within it a key survival of the old order. This may well account for some of the difficulties that science has in connection with relativistic theories, both special and general. The implicate order, however, has the possibility of opening up very different approaches in which these difficulties may perhaps hot arise.
Analogies like that of the ink drop are, however, limited because the actual particles that make up the ink droplet themselves move in an explicate way, even though the development of the droplet itself may be quite complex. A better analogy to the behavior of an electron, for example, can be obtained by considering a hologram which is a photographic record of light waves that have been reflected from an object.
In normal photography a lens is used to focus light from an object, so that each small section of the object is reproduced in a small section of the photographic plate. In holography, however, the photographic record made by laser light does not in fact resemble the object but consists of a fine pattern of interference fringes. Each portion of the plate now contains information from the whole of the object. When similar laser light is used to illuminate the plate, the light waves emerging from it resemble those that originally came from the object. It is therefore possible to see, in three dimensions, an image of the original object. What is particularly significant, however, is that even if only a part of the plate is illuminated, and image of the whole object is still obtained. This is because light from every part of the object is enfolded within each region of the plate. In normal photography, information is stored locally, but with the holograph it is stored globally. As successively smaller regions of the holograph are illuminated, the images as a whole are not lost. Instead fine detail becomes progressively more difficult to resolve. This global property of enfoldment of information and detail has something in common with both fractal and Fourier order.
The hologram provides a good analogy to the general nature of movement according to quantum mechanics. This movement is described mathematically by what is called a Green’s function, which can be thought of as representing a summation of very many waves, similar in some sense to those that scatter off an object. It is possible to obtain an intuitive picture of the meaning of the green’s function by considering what is known as a Feynman diagram. This is a representation of the movement of waves in terms of a diagrammatic structure of lines.
To start, consider a wavelet that emanates from a fixed point P:
/// Diagram (p. 176)
The lines radiating from P show how the wavelet spreads from this point. Now consider any point Q, at which the wavelet from P arrives. This in turn is the source of another wavelet which spreads as follows:
/// Diagram (p.176)
In this way the point R is reached, which itself becomes the source of yet another wavelet and so on. The essential idea is that each point is reached by wavelets, from all other points. In turn it becomes the source of a wavelet, proportional in strength to that of the wave that reaches it. Evidently there is a basic notion of order here, because the differences in any given step are similar to those of the next, and so on.
Now look at this process as a whole, and begin by considering all those waves, emanating from A and arriving at B, after a large number n of intermediate steps. Below is a typical path that connects A and B.
/// Diagram (p. 177)
The total wave at B is the sum of the contributions of all possible paths of this kind that connect A and B.
This way of looking at wave movement was proposed originally by C. Huygens in the eighteenth century, but around 1950, R. P. Feynman developed his diagrammatic representation of the approach of Huygens. The result was a very powerful new tool for dealing with quantum mechanical field theory.
At first Feynman did not intend this simply to be a tool, for he hoped that it would provide physical insight into quantum processes. Indeed, the informal language used in connection with Feynman diagrams, i.e., that they are the definite “paths” of particles, would suggest that such physical insight is possible. However, these diagrams actually represent only the contributions of different wavelets, which may add or subtract to produce interference effects, and so they are not coherent with the idea that a particle actually follows such a path. Since the electron not only is a wave but also has a particle nature, the Feynman diagram cannot provide an adequate image of the actual movement from whichever standpoint they are regarded.
What was left to physicists therefore was only to look at these diagrams as being an extremely useful tool in performing certain difficult calculations. However, it may turn out that Feynman’s original intuition may have some further meaning which has not yet been seen. Perhaps the implicate order will be relevant to this.
Returning to the consideration of the implicate order: Evidently the Feynman diagrams give an imaginative picture of a wave motion. In this picture, wavelets can be seen unfolding from each point toward the whole. Yet the very same movement can also be thought of as wavelets enfolding toward each point from the whole, as shown in the diagram.
/// Diagram (p. 178)
The basic movement of enfoldment and unfoldment is thus a dual on in which there is ultimately no separation between enfoldment and the unfoldment. The movement has the order of similar differences of degrees of enfoldment and unfoldment that has already been indicated. It therefore provides an example of the implicate order or enfolded order, which is described mathematically by the Green’s function and graphically by the corresponding Feynman diagrams.
Clearly this interpretation of the Green’s function is ultimately an outcome of physical intuition, on the part of Feynman, so that the source of the ideas is not primarily in the mathematics. In quantum theory all movement is described in terms of Green’s functions in the way indicated above. It follows therefore that the basic movements and transformations of all matter and all fields are to be understood in terms of a process of this kind. It is even possible to obtain some fairly direct experience of how it takes place by considering that as a person sits in a room, light from all points in it must enfold together to enter the pupil of the eye. This complex information is then unfolded by the lens of the eye and the nervous system into a consciousness of the room as constituted out of extended objects in an explicate order. Indeed there is even evidence that the memory of this event will not be stored locally within the brain but is distributed in some global fashion that represents the implicate order.
More generally, with a telescope, the entire universe in space and time is enfolded within each region and can then be unfolded with the aid of lenses and cameras. At first sight it could be supposed that the light coming from all the stars would produce a totally disordered pattern of waves within any small region of space. Yet each region enfolds the whole universe. Indeed, it is just this process of enfoldment and unfoldment that allows scientists to learn about the whole of the universe, no matter where they may be in it.
In the usual way of thinking, something like an implicate order is tacitly acknowledged, but it is not regarded as having any fundamental significance. For example, processes of enfoldment, such as those described by the Green’s function, are assumed to be just convenient ways of analyzing what is basically a movement in the explicate order, in which waves are transmitted continuously through purely local contact of fields that are only infinitesimal distances away from each other. In essence, however, the main point of the implicate order is to turn this approach upside down, and to regard the implicate order as fundamental, while the explicate order is then understood as having unfolded from the implicate order.
This has been illustrated through the analogies of the ink droplets and of the hologram. It is possible to combine certain features of both these analogies by imagining a wave that comes to a focus in a small region of space and then disperses. This is followed by another similar wave that focuses in a slightly different position, then by another and another and so on indefinitely until a “track” is formed that resembles the path of a particle. Indeed the particles of physics are more like these dynamic structures, which are always grounded in the whole from which they unfold and into which they enfold, in contrast to the little billiard balls that are grounded only in their own localized forms.
It is necessary, however, to go further than this. Up to now particular kinds of entities, such as electrons and neutrons, have been discussed, each of which has its own implicate order. But there may be a further unknown set of entities, each having its implicate order, and beyond this there may be a common implicate order, which goes deeper and deeper without limit and is ultimately unknown. This unknown and undescribable totality will be called the holomovement. It acts as the fundamental ground of all matter. As in the case of the analogy, in which a particle i taken to be a succession of wave pulses, so each object or entity emerges as a relatively stable and constant form out of the holomovement and into the explicate order. This form is sustained by the holomovement, into which it eventually dissolves. Therefore it must be understood primarily through this holomovement. It is clear that the implicate order ultimately prevails, although it is always in an essential relationship with the explicate order.
The Superimplicate Order (p.180)
The discussion based on the hologram provides only a limited view of the implicate order because it is based on a classical treatment of the transformations within a light wave. To obtain a deeper and more extensive understanding of the implicate order, it is necessary to start from quantum mechanical field theory. This is, in essence, the most basic and general form of the modern quantum theory that is available today. Such a step will lead to an extension of the implicate order, called the superimplicate order. This is much subtler than the implicate order and goes deeper. In addition, it is capable of further extension in ways that go beyond quantum theory altogether.
As with the quantum mechanical particle theory, it is necessary to proceed from the standpoint that the mathematical formalism of the quantum field theory is essentially correct, at least within some suitable limits. However, the informal language describing physical concepts is even more unclear in the field theory than it is in the particle theory.
The casual interpretation will therefore be extended in order to obtain a clear physical notion of the quantum field theory, as well as to gain insight into the superimplicate order.
To be more specific, the key new property treated by quantum field theory is the appearance of discrete particle-like quanta, in what was initially assumed to be a continuous field. In certain ways this process is similar to what was described in the analogy of a wave that focuses in a succession of small regions and thus resembles the track of a particle. In other ways, however, it is quite different so that this analogy, too, is limited. But in the causal interpretation, a clear and well-defined physical concept of the appearance of discrete particle-like quanta in a continuous field can be given. This interpretation fully and faithfully expresses the meaning of the mathematical equations.
It must be emphasized, however, that although the particular example of the superimplicate order is obtained from the causal interpretation of quantum field theory, the essential idea of the superimplicate order is not restricted either to the causal interpretation or to the quantum theory itself. Rather, these are only special forms of the more general superimplicate order.
The basic discussion of quantum field theory in terms of the implicate order and the causal interpretation is quite simple. Instead of taking a particle as the fundamental reality, start with the field. And instead of having a particle acted on by a quantum potential, suppose that the field is acted on by a superquantum potential. This superquantum potential is far subtler and more complex than the quantum potential, yet the basic principles governing the behavior are similar. Its net effect is to modify the field equations in a fundamental way so they become nonlinear and nonlocal. This brings about the new quantum properties of the field.
[…]
The Relationship Between the Implicate Order and the Generative Order (p.184)
The implicate order and the generative order are very closely related. Indeed, the implicate order may be understood as a particular case of the generative order. Thus, in the discussion of the Green’s function, it is possible to see how explicate forms are generated in an order of unfoldment, step by step. In this process, the whole is relevant to each part, unlike the case of fractals where the details are generated from local forms belonging only to the next less detailed stage of generation. While the implicate order is similar in a certain way to the order of fractals, it is much more extensive and subtle, since the process of unfoldment is related to the whole and not to a local order of space.
There is, however, a much more fundamental sense in which the implicate order is a generative order. For in quantum field theory, and the computer game analogy, the second implicate order is basically the source from which the forms of the first implicate order are generated. If there are higher implicate orders, then a similar generative order will prevail throughout all the levels. Ultimately, it is, of course, the holomovement, and what may lay beyond, from which all is generated.
The Implicate Order and Consciousness (p.185)
So far only material processes have been discussed in terms of the implicate order. But conscoiusness is much more of the implicate order than is matter. This is brought out in some detail in David Bohm’s Wholeness and the Implicate Order. A few of the main points discussed in that book, along with some further notions on the relationship between mind and matter will be presented here.
First of all, it is clear that thought is definitely in the implicate order. The very word implicate, meaning enfolded, suggests that one thought enfolds another and that a train of thought is actually a process of enfoldment of a succession of implications. This is not entirely dissimilar to the process described by a Green’s function, or to what takes place in the video game. In addition, thoughts and feelings unfold into each other, and these in turn give rise to dispositions that unfold into physical actions and on to more thoughts and feelings.
Language is also an enfolded order. Meaning is enfolded in the structure of the language, and meaning unfolds into thought, feeling, and all the activities that have already been discussed. In communication, meaning unfolds into the whole community and unfolds from the community into each person. Thus, there is an internal relationship of human beings to each other, and to society as a whole. The explicate form of all this is the structure of society, and the implicate form is the content of the culture, which extends into the consciousness of each person. What is seen on one side as society and the explicate forms of culture enfolds inseparably within what is seen on the other side as the consciousness of each individual in the society. For example, the laws and customs and limitations of the society do not actually operate as external forces that are alien to the people on whom they act. Rather, they are the expression of the very nature of these people, and in turn, they enfold to contribute to this nature.
Evidently, the implicate order of consciousness operates on many levels, which are related to each other as are the implicate and superimplicate order of the quantum field, and of the computer game. For example, as in the discussion of reason in the previous chapters, it was shown how one level of thought will organize the next level. This can go on to produce a structure that may develop indefinitely with relatively closed loops of many kinds. This implies that consciousness is organized through a generative order whose totality is in many ways similar to the totality of the generative and implicate order that organizes matter.
It is now possible to look into the question of how consciousness and matter are related. One possibility is to regard them as two generative and implicate orders, like separate but parallel streams that interrelate in some way. Another possibility is that basically there is only one order, whose ground includes the holomovement and may go beyond. This order will unfold into the two orders of matter and mind, which, depending on the context, will have some kind of relative independence of function. Yet at a deeper level they are actually inseparable and intervowen, just as in the computer game the players and the screen are united by participation in common loops. In this view, mind and matter are two aspects of one whole and no more separable than are form and content.
The Explicate and Sequential Limits of the Implicate and Generative Orders (p.186)
[…]
Summary and Conclusion (p.190)
This chapter moved beyond the idea of a sequential order, to introduce the notion of a generative order. The first example was in terms of fractals. Following this, it was shown how the generative order is relevant to creativity in art and to the creative perception and understanding of nature. The next step was to go into the implicate order, showing how it leads to the superimplicate order, which organize the lower ones, while capable of being affected by them. In this way it became apparent that the implicate order is a very rich and subtle generative order. Finally, consciousness was discussed as a generative and implicate order, and through this, notions of how mind and matter are related were proposed. In the final chapters, this approach will be extended to throw light on nature, mind, and society in a general way. This will help to open the door to a kind of dialogue that may creatively meet the breakdown of order that humanity is experiencing in its relationships in all these fields.
Chapter 5: GENERATIVE ORDER IN SCIENCE, SOCIETY AND CONSCIOUSNESS
[…]
Generative Order in Physics and in Cosmology (p.193)
[…]
The Generative Order of Life and Its Evolution (p.200)
[…]
The Generative Order in Society (p.204)
[…]
Consciousness and Matter (p.210)
[…]
Awareness and Attention (p.212)
[…]
Creative Intelligence (p.216)
[…]
The Brain and Artificial Intelligence (p.220)
Within the current, generally mechanistic and reductionist, worldview of science, it is only natural that a serious attempt should be made to model the function of the brain on some extension of what is now meant by a computer. This has led to the attempt to develop what is called artificial intelligence, a field that is associated with several different approaches, some of which are quite subtle. For example, the field of cognitive psychology includes the study of perception, language, problem solving, and concept formation. Other research fields combine with the neurosciences, particularly in the areas of vision and motor control. Other lines of investigation are leading scientists to develop computers that are far more sophisticated than those in use today. For example, there are “massively parallel” computers, analog systems, and computer languages that deal with concepts directly and are able to examine their own strategies and goals. Such research has great value, but much of it seems to be based on postulates that are of a generally reductionist nature. One of these is that all cognitive processes can ultimately be revealed through sufficiently subtle experiments and from inferences that are drawn from these investigations. Another assumption, perhaps more fundamental, is that at some stage scientists will come to the end of this cognitive analysis, or if not, then what lies beyond will not be particularly significant.
It should be clear that these assumptions, where cognitive processes are based on the intellect alone, are not in harmony with the approach taken in this book. Clearly this does not capture the essence of the whole generative order of the mind. Very probably it will be possible to simulate an unlimited number of aspects of the intellect, which is after all a relatively mechanical crystallization of the intelligence. In this sense, the proper description of these studies should be called artificial intellect.
However, if scientists still claim that artificial intelligence and not artificial intellect is genuinely involved in their researches, then certain important questions must be answered, some of which are indeed already being considered by researchers in this field. The basic problem is similar to that which is also encountered in human consciousness: How is it possible to question fundamental assumptions that have been fixed as necessary for the whole system of operations within the computer? In the case of a computer, programs and strategies correspond to fixed tacit assumptions in the mind. But these assumptions are just what must change in an appropriate way to meet the challenge of new and hitherto unknown situations.
One solution is to have additional “higher order” internal or external computers that could control these changes. But these machines would themselves also contain fixed elements in their programs that would in turn be required to change.
Moreover, the design of these fixed elements, as well as indeed that of the whole system, depends on a host of further assumptions made by the designers, most of which are part of the tacit infrastructure of the general consciousness of humanity. For example, in planning how to deal with a given problem, it is generally taken for granted, without any explicit discussion, that the current laws of physics and chemistry will be valid in any situation that may come up. To provide an adequate simulation of human intelligence, the computer would have to be able to become “aware” of such implicit assumptions, and to question them when necessary. This, however, would require that the computer be able to uncover and question the whole tacit and largely “unconscious” basis of the society in which it was made.
To the extent that human intelligence is able to confront such questions adequately, there is free play in thought and a corresponding free movement in awareness and attention, which makes possible the action of creative intelligence. How could this be simulated by a computer? One suggestion is to introduce random changes in some of its basic programs and strategies. However, as with Darwinian evolution, such “mutations” would for the most part be inappropriate and destructive. A possible way to deal with this would be to suggest that only those programs or strategies should survive that best fit the environment. But here, the criterion or selection has simply been externalized to include, for example, the scientists themselves, or else the human society with its requirements. If the computer itself is justifiably to be called intelligent, then it would have to contain its own internal criteria for what is beneficial or “fitting.” As far as can now be seen, this again would have to be preprogrammed, and in facing a new situation it is just these very criteria which themselves may have to change. This recalls Kuhn’s notion of a scientific revolution in which the criteria for judging theories are themselves subject to change.
Moreover, it can be called into question whether random mutations, of the kind discussed here, can ever give rise to totally “creative” perceptions, of the kind experienced by Bach and Mozart. This question is related to an earlier one of whether large changes in animal species can be accounted for by random mutation in DNA. In that connection it was suggested that major changes may have their origin in “hidden” orders, beyond those that are now studied in terms of current physics and chemistry. More generally it was proposed that creative intelligence originates in the subtle depths of the generative order, beyond anything that could be specified in terms of well-defined concepts at all. It is there, too, that the free play of thought and the free movement of awareness and attention have their ultimate ground. It does not seem possible for any novel design of computer or language to simulate such freedom adequately, although it may be capable of providing significant development within the relatively limited area of artificial intellect. In conclusion, it should be clear that creative intelligence cannot be grasped by the intellect in any form and that it will necessarily elude all such attempts to capture it in this way.
Creative Intelligence, Time, and the Timeless Order (p.223)
[…]
Summary and Conclusions (p.227)
[…]
Chapter 6: CREATIVITY IN THE WHOLE OF LIFE
In the previous chapter it was suggested that the potential for creativity is natural but that an excessively rigid attachment to fixed “programs” in the tacit infrastructure of consciousness is primarily what prevents this creativity from acting. The present chapter will explore the nature of these blocks in greater detail, and the social and cultural conditioning that lies behind them. This leads to a discussion of free dialogue, which is proposed as a key activity in which this sort of conditioning can be dissolved. Such free dialogue is fundamentally relevant to the whole question of how conditioning of the individual and of humanity, to falseness at the sociocultural level, can come to an end.
This chapter also contrasts the approaches of East and West to these important questions and suggests that a new order is in fact needed which goes beyond both. Finally the overall planetary culture is discussed in terms of three basic attitudes of mind to the whole of life: the scientific, the artistic, and the religious. The main purpose of the book is then summed up in a discussion suggesting what would be involved in a general release of human creative energies.
Creativity and What Blocks It (p.230)
In the Introduction, a call was made for a new surge of creativity in science. By now it will be clear that such a surge must extend into all areas of human activity if the actual challenge, which has finally revealed itself, is to be met. But does this mean that creativity must somehow be elicited from an organism that does not have in itself a natural potential for creativity? Desmond Morris, published in The Biology of Art (Methuen, London, 1962) In one experiment chimpanzees were given canvas and paint and immediately began to apply themselves to make balanced patterns of color, somewhat reminiscent of certain forms of modern art, such as abstract impressionism. The significant point about this experiment is that the animals became so interested in painting and it absorbed them so completely that they had comparatively little interest left for food, sex, or the other activites that normally hold them strongly. Additional experiments showed somewhat similar results for other primates. When very young children are given paints, their behavior is remarkably like that of the chimpanzees.
This seems to indicate that creativity is a natural potential. Yet somehow, in most cases, the urge to create fades as the human being gets older. Or at best it continues in certain limited areas, such as science, music, or painting. Why should this happen?
An extension of Morris’s experiment involved rewarding the chimpanzees for producing their paintings. Very soon their work began to degenerate until they produced the bare minimum that would satisfy the experimenter. A similar behavior can be observed in young children as they become “self-conscious” of the kind of painting they believe they are “supposed” to do. This is generally indicated to them by subtle and implicit rewards, such as praise and approval, and by the need to conform to what other children around them are doing. Thus creativity appears to be incompatible with external and internal rewards or punishments. The reason is clear. In order to do something for a reward, the whole order of the activity, and the energy required for it, are determined by arbitrary requirements that are extraneous to the creative act itself. This activity then turns into something mechanical and repetitious, or else it mechanically seeks change for its own sake. The state of intense passion and vibrant tension that goes with creative perception in the way discussed in Chapter 1 then dies away. The whole thing becomes boring and uninteresting, so that the kind of energy needed for creative perception and action is lacking. As a result, even greater rewards, or punishments, are needed to keep the activity going.
Basically, the setting of goals and patterns of behavior, which are imposed mechanically or externally, and without understanding, produces a rigid structure in consciousness that blocks the free play of thought and the free movement of awareness and attention that are necessary for creativity to act. But this does not mean that rules and external orders are incompatible with creativity, or that a truly creative person must live in an arbitrary fashion. To write a sonnet or a fugue, to compose an abstract painting, or to discover some new theorem in mathematics requires that creativity should operate within the context of a particular artistic or mathematical form. Cézanne‘s particular creativity in art, for example, was directed toward the discovery of new forms and orders of composition within the context of a particular form of freedom that had been previously established by the Impressionists. Some of Bach‘s greatest works are similarly created within the confines of strict counterpoint. To live in a creative way requires extreme and sensitive perception of the orders and structures of relationship to individuals, society, and nature. In such cases, creativity may flower. It is only when creativity is made subservient to external goals, which are implied by the seeking of rewards, that the whole activity begins to wither and degenerate.
Whenever this creativity is impeded, the ultimate result is not simply the absence of creativity, but an actual positive presence of destructiveness, as was suggested in Chapter 5. In the case of the painting experiment, this shows up as a false attitude. Both the chimpanzee and the child are engaged in an activity that no longer has meaning in itself, merely in order to experience a pleasant and satisfying state of consciousness, in the form of reward or the avoidance of punishment. This introduces something that is fundamentally false in the generative order of consciousness itself. For example, the continuation of this approach would eventually lead the child to seek pleasing words of praise from others, even if they are not true, and to collude with others in exchanging flattering remarks that lead to mutual satisfaction. This, however, is achieved at the expense of self-deception that can, in the long run, be quite dangerous.
What is even of greater danger to the child, in such an approach, is that it eventually brings about violence of various kinds. For creativity is a prime need of a human being and its denial brings about a pervasive state of dissatisfaction and boredom. This leads to intensive frustration that is conducive to a search for exiting “outlets,” which can readily involve a degree of force that is destructive. This sort of frustration is indeed a major cause of violence. However, what is even more destructive than such overt violence, is that the senses, intellect, and emotions of the child gradually become deadened and the child loses the capacity for free movement of awareness, attention, and thought. In effect, the destructive energy that has been aroused in the mind has been turned against the whole creative potential itself.
Most education does in fact make use, in explicit or in more hidden and subtle ways, of rewards and punishments as key motivating factors. For example, the whole philosophy of behavior modification and positive reinforcement, which is particularly prevalent in North American education, holds that a system of rewards is essential for effective learning. This alone is a tremendous barrier to creativity.
In addition, education has traditionally given great value to fixed knowledge and techniques. In this way it places extremely great importance on authority as determining the very generating order of the psyche. What is involved is not only the authority of the teacher as a source of knowledge that is never to be questioned, but even more, the general authority of knowledge itself, as a source of truth that should never be doubted. This leads to a fundamental loss of self-confidence, to a blockage of free movement and a corresponding dissipation of energy, deep in the generative order of the whole of consciousness. Later on, all of this may show up as a disposition to be afraid of inquiring into fundamental questions, and to look to experts and “geniuses” whenever any difficulty or basic problem is encountered.
Of course, a certain reasonable kind of authority is needed to maintain necessary order in the classroom. And the student has to realize that, in broad areas, the teacher has valuable knowledge that can be conveyed in an appropriate way. But what is important is the overall attitude to this knowledge. Does it seek to impose itself arbitrarily and mechanically deep withing the generative order of the mind, or does it allow itself to be discussed and questioned, with a view to making understanding possible? Similar questions can be raised with regard to conformity to arbitrary norms, which come not only from the teacher, but even more from the peer group and from society at large.
Beyond school, society operates in much the same way, for it is based largely on routine work that is motivated by various kinds of fear and by arbitrary pressures to conform as well as by the hope for rewards. Moreover, society generally regards this as necessary and valuable and, in turn, treats creativity as irrelevant for the most parts, except in those special cases, such as science and the arts, in which it is rewarded. In fact, no society has thus far managed to organize itself in a complex way without using a system of rewards and punishments as a major inducement to bring about cooperation. It is generally felt that if society tried to do without these, whether in the family, in the classroom, at work, or in broader contexts, it would incur the risk of eventual total disruption and chaos. Creativity is nevertheless a major need of each human being and the blockage of this creativity eventually threatens civilization with ultimate destruction.
Humanity is therefore faced with an urgent challenge of unparalleled magnitude. Specifically, rigidity in the generative order, to which control through rewards and punishments makes a major contribution, prevents the free play of thought and the free movement of awareness and attention. This leads to false play which ultimately brings about a pervasive destructiveness while at the same time blocking natural creativity of human beings.
A proper response to this challenge requires the kind of overall creativity in society that is implicit in the call being made in this book for a general creative surge in all areas of life. Clearly from this it would follow that the various forms of rigidity that have already been discussed would all change fundamentally. But such a change cannot be restricted to a single overall flash of insight. Creativity has to be sustained. For example, in Chapter 4 it was shown how the artist has to work constantly from the creative source in the generative order. An artist does not have a creative vision and then applies it mechanically, in a sequential process by means of rules, techniques, and formulae. Rather, these latter flow out of the sustained creative vision in a creative way.
To pay serious attention to this need for sustained creativity is extremely relevant for bringing about a creative change in culture and in society. In most cases, however, creative new discoveries are generally followed by an attempt to reduce them to something that can be applied mechanically. While mechanical application is necessary in certain contexts, the basic impetus for each individual must come from the creative origin, and this is beyond any mechanical, explicate, or sequential order of succession.
It is possible to point to specific areas in which a creative change would be of great benefit to society and the individual. For example, by means of a tremendous creative common action, education must no longer depend on rewards and punishments, no matter how subtle they may be. It must also cease to place an excessively high value on arbitrary authority, fixed knowledge, and techniques for conformity. Some partial and preliminary work in this direction has been done from time to time. For example, there has been an effort to present the child with a great deal of meaningful material to arouse interest, so that the child does not have to be offered a reward to learn. Also, some people working in this field have emphasized free play as a way of arousing creativity. Others have given much attention to relationships that avoid unnecessary authority and conformity. By the further development of such approaches, it should in principle be possible for children to learn without the inducement of rewards.
However, there are deeper difficulties, which prevent these approaches form actually working in the long run. The problem does not stem primarily from the field of education alone. Rather, it arises ultimately out of the tacit infrastructure of the entire consciousness of humanity. This is deeply and pervasively conditioned, for example, by general tradition that takes the absolute necessity of rewards and punishments for granted. Both teachers and students are caught up in subtler forms of the same false structure that they are explicitly trying to avoid. This may, in the long run, be at least as destructive as was the original pattern that the whole experiment in education was designed to avoid.
It seems that the whole conditioning of all who take part must in fact change: society, the family, and the individual. It is thus clear that there is no single stationary point at which these problems might be attacked. The educational system, society, and the individual are all intimately involved. But it is ultimately the overall order of human consciousness that has to be addressed.
Blocks to Creativity in the Generative Order of Society (p.235)
Creativity, in almost every area of life, is blocked by a wide range of rigidly held assumptions that are taken for granted by society as a whole. Some of these have already been discussed in this book, but in addition, every society holds additional assumptions that are of such a shaky nature that they are not even admitted into discussion. There is therefore an unspoken requirement that everyone must subscribe to these assumptions, but that no one should ever mention that any such assumptions indeed exist. They are tacitly denied as operating within society, and even this denial is denied. The overall effect is to lead people to collude in “playing false” so they constantly distort all sorts of additional thoughts in order to protect these assumptions. Such bad faith enters deep into the overall generative order of society.
These rigidities and fixed assumptions, many of which must not be mentioned but must nevertheless be defended, may be compared with a kind of pollution that is constantly being poured into the stream of the generative order of society. It makes no sense to attempt to “clean up” parts of this pollution farther downstream while continuing to pollute the source itself. What is needed is either to stop the pollution at its source, or to introduce some factor into the stream that naturally “cleans up” pollution.
In the body a similar problem arises. As a person grows older, through infection, allergies, contaminants, misadventure, and the process of aging, considerable “misinformation” or irrelevant information accumulates in the system. Indeed it is possible to look at a disease like cancer as arising from misinformation in the structure of DNA. Viruses also introduce misinformation, in the sense that DNA from the virus acts to replace some of the DNA in the host cell and therefore causes this cell to replicate foreign DNA rather than serving the needs of the body.
There are basically three ways of dealing with this problem of misinformation in the body. The first is to avoid the introduction of misinformation in the first place, for example, by keeping away from infection through good sanitation and a careful diet. Second, where misinformation exists, it may be possible to do something to remove it through various kinds of medical intervention. But more significantly, the third option involves the body itself, which possesses an immune system which is able to “clear up” misinformation in a natural way.
This is indeed the body’s main mode of dealing with misinformation. This can be clearly seen from the fact that drugs are of little use in treating a disease like AIDS, which destroys this immune system itself. Furthermore, the whole practice of immunization relies on activating the immune system and so avoiding the onset of particular diseases.
The immune system itself is particularly complex and contains a very subtle kind of information that can respond to the whole “meaning” of what is happening to the order of the body. In this way it is able to distinguish misinformation from information needed for the body’s healthy operation. It can be compared to a kind of “intelligence” that works within the body. Moreover, there is evidence that this sort of “intelligence” can respond to the higher levels that are usually associated with thought and feeling. It is well known that depressing thoughts can inhibit the activity of the immune system, with the result that a person becomes more susceptible to infections. Indeed there is much evidence that a vigorous, creative state of mind and a strong “will to live” are conducive to general health and even to recovery from dangerous illnesses. More generally, it could be said that good health is basically a manifestation of the overall creative intelligence, working in concert with the body, through various means that include exercise, diet, relaxation, and so on.
Returning to a consideration of society, clearly there is also a vast amount of misinformation in circulation which acts toward society’s degeneration. The media and various modern means of communication have the effect of rapidly disseminating and magnifying this misinformation, just as they do with valid information. It should be clear that by “misinformation” is meant a form of generative information that is inappropriate, rather than simply incorrect statements of fact. In a similar way a small “mistake” in the DNA can have disastrous consequences because it forms part of the generative order of the organism and may set the whole process in the wrong direction.
In society, the generative order is deeply affected by what has a very general significance. Indeed the generative order may be regarded as the concrete activity of the general. This takes the form of general principles, general aims and generally accepted values, attitudes, and beliefs of all kinds that are associated with the family, work, religion, and country. In going from these general principles to the universal, it is clear that the effect on the generative order will become yet more powerful. When a given principle is regarded as universally valid, it means that it is taken as absolutely necessary. In other words, things cannot be otherwise, under any circumstances whatsoever. Absolutely necessary means “never to yield.” To have something in the generative order that can never give way, no matter what happens, is to put an absolute restriction on free play of the mind, and thus to introduce a corresponding block to creativity that is very difficult to move.
Of course, both the individual and society require a certain stability, and for this, thought must be able to hold itself fixed within certain appropriate limits and with a certain kind of relative necessity.
Over a limited period of time, certain values, assumptions, and principles may usefully be regarded as necessary. They are relatively constant, although they should always be open to change when evidence for the necessity of the latter is perceived. The major problem arises, however, when it is assumed, usually tacitly and without awareness and attention, that these values, assumptions, and principles have to be absolutely fixed, because they are taken as necessary for the survival and health of the society and for all that its members hold to be dear.
In the beginning of this book it was argued that science, which is in principle dedicated to the truth, tends to be caught up in necessity which then leads to false play and a serious blockage of creativity. It is now clear that the assumptions of absolute necessity, with their predispositions to unyielding rigidity, are only part of a much broader spectrum of similar responses that pervade society as a whole. General principles, values, and assumptions, which are taken in this way to have absolute necessity, are thus seen as a major source of the destructive misinformation that is polluting the generative order of society.
As with the body, society attempts to deal with this sort of misinformation by trying to prevent it from entering its fabric, or attempting to “cure” it with some form of therapy. For example, on a rather superficial level, there are laws to prevent false information and information which may engender hatred, anger, and prejudice to be spread about various races, religions, and groups. Writers, dramatists, and filmmakers go some way to making people aware of prejudices and rigidly fixed attitudes. But in the long run, all these attempts are limited by the overwhelming and yet often very subtle, pressures within society toward colluding to defend one’s own group and its ideas. In addition, there is the whole problem of the intolerance and mistrust that have grown up between nations, religions, ideologies and other groups which go all the way down to the family itself. To some extent psychotherapy and group therapies can help to clear up individual misinformation of this kind, which may go back to early childhood, or start in a later phase of life. But these approaches have very little effect in the larger sphere of society as a whole.
A particularly important piece of misinformation is the key assumption that creativity is necessary only in specialized fields. This assumption pervades the whole culture, but most people are generally not aware of it; there is always a tendency for misinformation to defend itself by leading people to collude in playing false, whenever such an assumption is questioned. Assuming the restricted nature of creativity is obviously of serious consequence for it clearly predetermines any program that is designed to clear up the misinformation within society and suggests that it cannot be creative.
All that seems to be left is to ask whether society contains some kind of “immune system” that could spontaneously and naturally clear up misinformation. If such a system exists, then it is certainly not obvious, nor does it appear to be in common operation within our society today.
Dialogue and Culture (p.240)
In this section it is proposed that a form of free dialogue may well be one of the most effective ways of investigating the crisis which faces society, and indeed the whole of human nature and consciousness today. Moreover, it may turn out that such a form of free exchange of ideas and information is of fundamental relevance for transforming culture and freeing it of destructive misinformation, so that creativity can be liberated. However, it must be stressed that what follows is not given in the spirit of a prescription that society is supposed to follow. Rather it is an invitation to the reader to begin to investigate and explore in the spirit of free play of ideas and without the restriction of the absolute necessity of any final goal or aim. For once necessity and absolute requirements or directions enter into the spirit of this exploration, then creativity is limited and all the problems that have plagued human civilization will surface yet again to overwhelm the investigation.
To begin, it should be noted that many of the ideas to be explored were first investigated by Patrick de Maré, who is a psychiatrist working in England. De Maré has used his wide experience of dialogue in therapeutic groups to support his arguments. However, it is essential to emphasize that his ideas about dialogue are not concerned primarily with psychotherapy, but rather with the transformation of culture, along the general lines that have been indicated in this chapter.
In the first two chapters it was shown how rigid conditioning of the tacit infrastructure of scientific thought has led to a fragmentation in science and to an essential breakdown in communication between areas which are considered to be mutually irrelevant. Nevertheless a closer investigation of actual cases suggested that there is nothing inherent in science which makes such breaks in communication and fragmentation inevitable. Indeed wherever fragmentation and failures in communication arise, this clearly indicates that a kind of dialogue should be established.
The term dialogue is derived from a Greek word, with dia meaning “through” and logos signifying “the word.” Here “the word” does not refer to mere sounds but to their meaning. So dialogue can be considered as a free flow of meaning between people in communication, in the sense of a stream that flows between banks.
A key difference between a dialogue and an ordinary discussion is that, within the latter, people usually hold relatively fixed positions and argue in favor of their views as they try to convince others to change. At best this may produce agreement or compromise, but it does not give rise to anything creative. Moreover, whenever anything of fundamental significance is involved, then positions tend to be rigidly nonnegotiable and talk degenerates either into a confrontation in which there is no solution, or into a polite avoidance of the issues. Both these outcomes are extremely harmful, for they prevent the free play of thought in communication and therefore impede creativity.
In dialogue, however, a person may prefer a certain position but does not hold to it nonnegotiably. He or she is ready to listen to others with sufficient sympathy and interest to understand the meaning of the other’s position properly and is also ready to change his or her own point of view if there is good reason to do so. Clearly a spirit of goodwill or friendship is necessary for this to take place. It is not compatible with a spirit that is competitive, contentious, or aggressive. In the case of Einstein and Bohr, which was discussed in Chapter 2, these requirements were evidently met, at least initially. However, because each felt that a different notion of truth and reality was involved, which was not negotiable in any way at all, a real dialogue could never take place.
This brings us to an important root feature of science, which is also present in dialogue: to be ready to acknowledge any fact and any point of view as it actually is, whether one likes it or not. In many areas of life, people are, on the contrary, disposed to collude in order to avoid acknowledging facts and points of view that they find unpleasant or unduly disturbing. Science is, however, at least in principle, dedicated to seeing any fact as it is, and to being open to free communication with regard not only to the fact itself, but also to the point of view from which it is interpreted. Nevertheless, in practice, this is not often achieved. What happens in many cases is that there is a blockage of communication.
For example, a person does not acknowledge the point of view of the other as being a reasonable one to hold, although perhaps not correct. Generally this failure arises when the other’s point of view poses a serious threat to all that a person holds dear and precious in life as a whole.
In dialogue it is necessary that people be able to face their disagreements without confrontation and be willing to explore points of view to which they do not personally subscribe. If they are able to engage in such a dialogue without evasion or anger, they will find that no fixed position is so important that it is worth holding at the expense of destroying the dialogue itself. This tends to give rise to a unity in plurality of the kind discussed in Chapter 3. This is, of course, quite different from introducing a large number of compartmentalized positions that never dialogue with each other. Rather, a plurality of points of view corresponds to the earlier suggestion that science and society should consist not of monolithic structures but rather of a dynamic unity within plurality.
One of the major barriers to this sort of dialogue is the rigidity in the tacit infrastructure of the individual and society, which has been discussed throughout this book. The tacit infrastructure of society at large is contained in what is generally called culture. Within each society, however, there are many subcultures which are all somewhat different, and which are either in conflict with each other, or more or less ignore each other as having mutually irrelevant aims and values. Such subcultures, along with the overall culture, are generally rigidly restricted by their basic assumptions, most of which are tacit and not open to awareness and attention. Creativity is therefore, at best, an occasional occurrence, the results of which are quickly absorbed in a fairly mechanical way into the general tacit infrastructure.
At present, a truly creative dialogue, in the sense that has been indicated here, is not at all common, even in science. Rather the struggle of each idea to dominate is commonly emphasized in most activities in society. In this struggle, the success of a person’s point of view may have important consequences for status, prestige, social position, and monetary reward. In such a conditioned exchange, the tacit infrastructure, both individually and culturally, responds very actively to block the free play that is needed for creativity.
The importance of the principle of dialogue should now be clear. It implies a very deep change in how the mind works. What is essential is that each participant is, as it were, suspending his or her point of view, while also holding other points of view in a suspended form and giving full attention to what they mean. In doing this, each participant has also to suspend the corresponding activity, not only of his or her own tacit infrastructure of ideas, but also of those of the others who are participating in the dialogue. Such a thoroughgoing suspension of tacit individual and cultural infrastructures, in the context of full attention to their contents, frees the mind to move in quite new ways. The tendency toward false play that is characteristic of the rigid infrastructures begins to die away. The mind is then able to respond to creative new perceptions going beyond the particular points of view that have been suspended.
In this way, something can happen in the dialogue that is analogous to the dissolution of barriers in the “stream” of the generative order that was discussed at the end of the previous chapters. In the dialogue, these blockages, in the form of rigid but largely tacit cultural assumptions, can be brought out and examined by all who take part. Because each person will generally have a different individual background, and will perhaps come from a different subculture, assumptions that are part of a given participant’s “unconscious” infrastructure may be quite obvious to another participant, who has no resistance to seeing them. In this way the participants can turn their attention more generally to becoming aware, as broadly as possible, of the overall tacit infrastructure of rigid cultural and subcultural assumptions and bringing it to light. As a result, it becomes possible for the dialogue to begin to play a part that is analogous to that played by the immune system of the body, in “recognizing” destructive misinformation and in clearing it up. This clearly constitutes a very important change in how the mind works.
There is, however, another extremely important way in which the operation of the mind can be transformed in such a dialogue. For when the rigid, tacit infrastructure is loosened, the mind begins to move in a new order. To see the nature of this order, consider first the order that has traditionally characterized cultures. Essentially this involves a strong fragmentation between individual consciousness–“what the individual knows all together”–and social consciousness–“what the society knows all together.”
For the individual, consciousness tends to emphasize subjectivity in the sense of private aims, dreams, and aspirations that are shared to some extent with family and close friends, as well as a general search for personal pleasure and security. In society, however, consciousness tends to emphasize a kind of objectivity with common aims and goals, and there is an attempt to put conformity and the pursuit of the common welfare in the first place. One of the principal conflicts in life arises therefore in the attempt to bring these two fragments together harmoniously. For example, as a person grows up, he (or she) may find that his individual needs have little or no place in society. And in turn, as society begins to act on the individual consciousness in false and destructive ways, people become cynical. They begin to ignore the requirements of reality and the general good in favor of their own interests and those of their group.
Within this generally fragmentary order of consciousness, the social order of language is largely for the sake of communicating information. This is aimed, ultimately, at producing results that are envisaged as necessary, either to society or to the individual, or perhaps to both. Meaning plays a secondary part in such usage, in the sense, for example, that what are put first are the problems that are to be solved, while meaning is arranged so as to facilitate the solution of these problems. Of course, a society may try to find a common primary meaning in myths, such as that of the invincibility of the nation or its glorious destiny. But these lead to illusions, which are in the long run unsatisfactory, as well as dangerous and destructive. The individual is thus generally left with a desperate search for something that would give life real meaning. But this can seldom be found either in the rather crude mechanical, uncaring society, or in the isolated and consequently lonely life of the individual. For if there is not common meaning to be shared, a person can be lonely even in a crowd.
What is especially relevant to this whole conflict is a proper understanding of the nature of culture. It seems clear that in essence culture is meaning, as shared in society. And here “meaning” is not only significance but also intention, purpose, and value. It is clear, for example, that art, literature, science, and other such activities of a culture are all parts of the common heritage of shared meaning, in the sense described above. Such cultural meaning is evidently not primarily aimed at utility. Indeed, any society that restricts its knowledge merely to information that it regards as useful would hardly be said to have a culture, and within it, life would have very little meaning. Even in our present society, culture, when considered in this way, appears to have a rather small significance in comparison to other issues that are taken to be of vital importance by many sectors of the population.
The gulf between individual consciousness and social consciousness is similar to a number of other gulfs that have already been described in this book, for example, between descriptive and constitutive orders, between simple regular orders of low degree and chaotic orders of infinite degree, and, of course, between the timeless and time orders. But in all these cases, broad and rich new areas for creativity can be found by going to new orders that lie between such extremes. In the present case, therefore, what is needed is to find a broad domain of creative orders between the social and individual extremes. Dialogue therefore appears to be a key to the exploration of these new orders.
To see what is involved, note that as the above dialogue develops, not only do specific social and cultural assumptions “loosen up,” but also much deeper and more general assumptions begin to be affected in a similar way. Among these, one of the most important is the assumption that between the individual consciousness and the social consciousness there is an absolute gulf. This implies that the individual must adjust to fit into the society, that society must be remade to suit the individual, or that some combination of both approaches must be carried out. If, however, the dialogue is sustained sufficiently, then all who participate will sooner or later be able to see, in actual fact, how a creative movement can take place in a new order between these extremes. This movement is present both externally and publicly, as well as inwardly, where it can be felt by all. As with alert attention to a flowing stream, the mind can then go into an analogous order. In this order, attention is no longer restricted to the two extreme forms of individual and social. Rather, attention is transformed so that it, along with the whole generative order of the mind, is in the rich creative domain “between” these two extremes.
The mind is then capable of new degrees of subtlety, moving from emphasis on the whole group of participants to emphasis on individuals, as the occasion demands. This is particularly significant for proper response to the strong emotional reactions that will inevitably arise, even in the friendliest group, whenever fundamental assumptions are disturbed. Because the mind is no longer rigidly committed to the individual or to the social extremes, the basic issues that arise in a disagreement between participants are to a considerable extent “defused.” For the assumptions that are brought to the common attention are no longer implied to have absolute necessity. And as a result, the “emotional charge” that is inevitably associated with an assumption that is dear to one or more members of the group can be reduced to more manageable proportions, so that violent “explosions” are not likely to take place. Only a dialogue that can, at the same time, meet the challenge both of uncovering the intellectual content of a rigidly held basic assumption and of “defusing” the emotional charge that goes with it will make possible the proper exploration of the new order of mental operation that is being discussed here.
It is possible to have such dialogues in all sorts of circumstances, with many or just a few people involved. Indeed even an individual may have a kind of internal dialogue with himself or herself. What is essential here is the presence of the spirit of dialogue, which is, in short, the ability to hold many points of view in suspension, along with a primary interest in the creation of a common meaning. It is particularly important, however, to explore the possibilities of dialogue in the context of a group that is large enough to have within it a wide range of points of view, and to sustain a strong flow of meaning. This latter can come about because such- a dialogue is capable of having the powerful nonverbal effect of consensus. In the ordinary situation, consensus can lead to collusion and to playing false, but in a true dialogue there is the possibility that a new form of consensual mind, which involves a rich creative order between the individual and the social, may be a more powerful instrument than is the individual mind. Such consensus does not involve the pressure of authority or conformity, for it arises out of a spirit of friendship dedicated to clarity and the ultimate perception of what is true. In this way the tacit infrastructure of society and that of its subcultures are not opposed, nor is there any attempt to alter them or to destroy them. Rather, fixed and rigid frames dissolve in the creative free flow of dialogue as a new kind of microculture emerges.
People who have taken part in such a dialogue will be able to carry its spirit beyond the particular group into all their activities and relationships and ultimately into the general society. In this way, they can begin to explore the possibility of extending the transformation of the mind that has been discussed earlier to a broader sociocultural context. Such an exploration would clearly be relevant for helping to bring about a creative and harmonious order in the world. It should be clear by now that the major barriers to such an order are not technical; rather they lie in the rigid and fragmentary nature of our basic assumptions. These keep us from changing in response to the actual situations and from being able to move together from commonly shared meanings.
The Individual, the Social, and the Cosmic Dimensions of the Human Being (p.248)
[…]
The Responses of East and West to the Conditioning of Consciousness (p.255)
[…]
Creativity in Science, Art, and Religion (p.260)
[…]
A New Order of Creativity (p.265)
[…]
Summary and Outlook (p.268)
[…]
/////// End of Quote from Bohm and Peat