Physics and its Models

This page is a sub-page of the page on our Learning Object Repository.

///////

The sub-pages of this page are:

• Science, Order, and Creativity
• Physics – The Pioneer Science
• Ideas of Space and Place
• Mathematical and Physical Geometry
• New Foundations for Classical Mechanics
• Molten-Salt Thorium Nuclear Reactors

///////

Related KMR-pages:

• David Hestenes on Modeling
• Modeling and Mapping
• Disagreement Management
• Geometric Optics
• Solar simulator
• Stereographic Projection
• The Mercator Projection
• Geometric Optics

///////

Books:

• New Foundations for Classical Mechanics,
David Hestenes (1993, (1986)), ISBN 90-277-2090-8.
• Science, Order, and Creativity – A Dramatic New Look at the Creative Roots of Science and Life, by David Bohm and F. David Peat, Bantam Books, 1987.

///////

Other related sources of information:

• The most important math formula for understanding physics.
• A Modeling Primary on Methods and Techniques for Communicative Modeling
and Disagreement Management. [TEL-Map D1.1, Febr. 2011]
• Dimensional Analysis
• Conversion of units
• The kilogram: The world’s roundest object
• PUM: Physics Union Mathematics
• Gravity visualized
• Visualization of the Coriolis and Centrifugal forces
• The Mercator Projection
• Applications in Physics

• Physics marble track review part one // Homemade Science with Bruce Yeany
• Amazing Science Toys / Gadgets 1
• Amazing Science Toys / Gadgets 2
• Amazing Science Toys / Gadgets 3
• Amazing Science Toys / Gadgets 4
• Amazing Science Toys / Gadgets 5
• Amazing Science Toys / Gadgets 6

///////

• Amazing physics toys that will surprize you (at Brilliant.org)
• Math and Science done right (at Brilliant.org)

///////

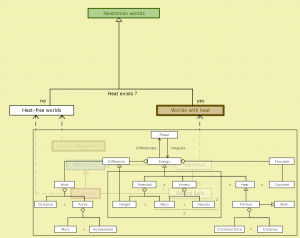
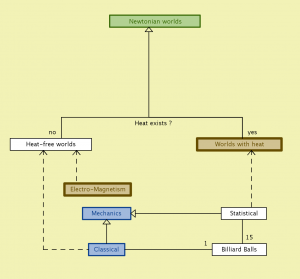
Newtonian worlds:

Newtonian worlds (with metadata):

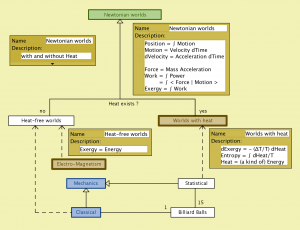
Newtonian worlds – peeking into Classical Mechanics:

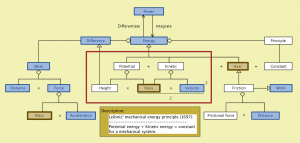
Mechanical energy (with Leibniz mechanical energy conservation principle):

Newtonian worlds – peeking into worlds with heat:

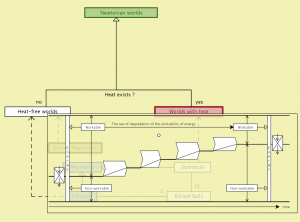
Worlds with heat – the decreasing workpower of energy:

///////

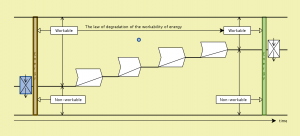
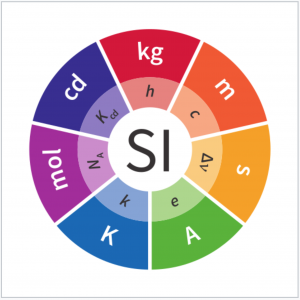
The seven base units of the SI system:

The seven defining constants of the SI system:

The logo of the SI system (from BIPM):

Four basic and some derived units of the SI system:

///////

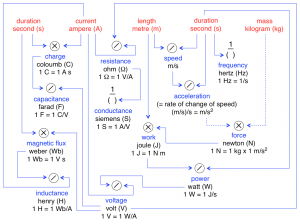
The SI system units for Area, Volume, and Pressure:

///////

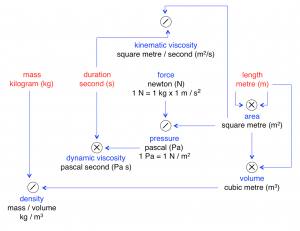
Is mathematics discovered or invented?

I will also comment on a thematic thread that runs through the book (Siffrorna i våra liv) and which concerns the philosophical question of the interplay between the concrete and the abstract. This question is closely related to the question of whether mathematics is “discovered” (as the platonists claim) or “invented” (as the intiutionists prefer to believe).

In his book “Are Numbers Real? – The Uncanny Relationships between Mathematics and the Physical World” the science journalist Brian Clegg presents an “intermediate” perspective. I the final paragraph of the book he writes:

=======
“As we have seen in our journey in this book, from the mathematician’s viewpoint, fractions and geometry are just the beginning of vast landscapes of awesome mathematical power and splendor. They are landscapes where mathematicians can spend their entire lifetimes exploring without ever coming across anything that could be considered to be real. Sometimes, though, the mathematical structures and mechanisms do parallel the real world. Such numbers and procedures may not actually be real, but they can still help answer our questions.

Despite its ability for abstraction, we need to keep our practical mathematics grounded in the physical so that the language of science can speak to us all. To come back to the question in the title of the book – numbers, I would suggest, are real at their most basic, but most of mathematics isn’t. It’s a fantasy world that sometimes mirrors and parallels our own, and as such can help provide us with tools to help us understand reality. But it needs to be kept in place. And as long as we (as scientists) remember this, we can’t go far wrong.”
=======

///////

Physically and mentally augmented senses

Bohm and Peat: Science, Order, and Creativity: A dramatic new look at the creative roots of science and life by David Bohm and F. David Peat.

///////

Hestenes on Conceptual Learning 1:

Hestenes on Conceptual Learning 2:

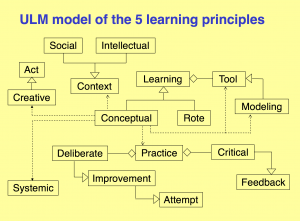
Hestenes on Conceptual Learning 3:

Hestenes on Conceptual Learning 4:

Hestenes on Conceptual Learning 5:

Hestenes on Conceptual Learning 6:

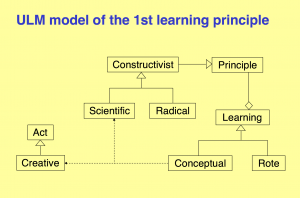
Hestenes on Conceptual Learning 7:

Hestenes on Conceptual Learning 8:

Hestenes on Conceptual Learning 9:

Hestenes on Conceptual Learning 10:

///////

Free-grazing lenses (Frigående glasögon):

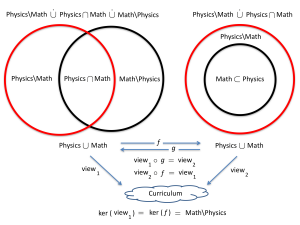
Situation 1 (top left) depicts a pair of normal eyeglasses that consists of two separate lenses joined together to enable two separate views ( $\, A_1 \,$ and $\, A_2 \,$ ) of the same object ( $\, A \,$ ).

In situation 2 (top right) the connection between the lenses has been removed and therefore they are free to view separate objects ( $\, A \,$ and $\, B \,$ ). Here we have two separate (= disjoint) lenses looking at two disjoint objects, and therefore

$\, A \cup B \; \equiv \; A \; \stackrel{\ldotp}{\cup} \; B$ .

In situation 3 (bottom left) we have neither $\, A \subset B \,$ nor $\, B \subset A \,$ .
Hence the union $\, A \cup B \,$ consists of three disjoint pieces:

$\, A \cup B \; \equiv \; A \cap B \; \stackrel{\ldotp}{\cup} \; A \setminus B \; \stackrel{\ldotp}{\cup} \; B \setminus A$ .

In situation 4 (bottom right) the view through one of the lenses “contains” (= dominates) the view through the other, and the viewer has in fact become “one-eyed.”
Since $\, B \subset A \,$ we have:

$\, A \cup B \; \equiv \; A \; \equiv \; B \; \stackrel{\ldotp}{\cup} \; A \setminus B$ .

Physics union Mathematics

///////

Excerpts from a mail exchange from Modeling Digest 19 June – 28 July 2019

Date: Fri, 21 Jun 2019 05:00:18 +0000
From: Jane Jackson <jane.jackson@asu.edu>
Subject: David Hestenes on the divorce of math from physics in the structure of the K-12 curriculum</jane.jackson@asu.edu>

David Hestenes is a deep thinker — and immensely creative. His thoughts on the intimacy between math and physics are expressed in two articles that you can freely download at the ASU modeling legacy website: modeling.asu.edu . Click on “Research & Evaluation”. Enjoy! Good summer reading: stimulating and enlightening. — Jane Jackson

1) Hestenes: Modeling Theory for Math and Science Education (2007).pdf
Dr. Hestenes wrote (on page 2): ” I submit that the single most serious deficiency in U.S. math education is the divorce of mathematics from physics in the education of mathematicians, in the training of math teachers, in the structure of the K–12 (–16–20) curriculum. Moreover, this is not a simple deficiency in the breadth of education; it is a fundamental problem in conceptual learning and cognition. I claim that cognitive processes for understanding math and physics are intimately linked and fundamentally the same! Indeed, I claim that physics is cognitively basic to quantitative science in all domains!!”

Ref: D. Hestenes, Modeling Theory for Math and Science Education, In R. Lesh, P. Galbraith, C. Hines, A. Hurford (eds.) Modeling Students’ Mathematical Competencies (New York: Springer, 2010).

2) Hestenes – Notes on Modeling.pdf
[page 25] … the most serious consequence of the divorce of mathematics from physics is the fact that, in the U.S. at least, most high school math teachers have little insight into relations of math they teach to science in general and physics in particular.

Here is a bit of data to support my contention: We administered the FCI to a cohort of some 20 experienced high school math teachers. The profile of scores was the same as the pitiful profile for traditional instruction in Fig. 10, with the highest score at the Newtonian threshold of 60%. Half the teachers missed basic questions about relating data on motion to concepts of velocity and acceleration.

This chasm between math and science, now fully ensconced in the teachers, may be the single most serious barrier to significant secondary science education reform.

Ref: D. Hestenes, Notes for a Modeling Theory of Science, Cognition and Physics Education. In E. van den Berg, A. Ellermeijer & O. Slooten (eds.) Modelling in Physics and Physics Education, (U. Amsterdam 2008).

[ …]

Topics of the day:

1. What are the connections between math and physics: is it just the use of symbols?
2. David Hestenes’ writing on V.I.Arnold: Mathematics is part of physics.

Dr. Hestenes wrote (on page 2): ” I submit that the single most serious deficiency in U.S. math education is the divorce of mathematics from physics in the education of mathematicians, in the training of math teachers, in the structure of the K–12 (–16–20) curriculum. Moreover, this is not a simple deficiency in the breadth of education; it is a fundamental problem in conceptual learning and cognition. I claim that cognitive processes for understanding math and physics are intimately linked and fundamentally the same! Indeed, I claim that physics is cognitively basic to quantitative science in all domains!!”

[…]

Date: Fri, 21 Jun 2019 21:04:42 -0700
From: Rob MacDuff <macduff@mac.com>
Subject: A need for change? </macduff@mac.com>

Jane posted this quote from David:
=====
Dr. Hestenes wrote (on page 2): ” I submit that the single most serious deficiency in U.S. math education is the divorce of mathematics from physics in the education of mathematicians, in the training of math teachers, in the structure of the K–12 (–16–20) curriculum. Moreover, this is not a simple deficiency in the breadth of education; it is a fundamental problem in conceptual learning and cognition. I claim that cognitive processes for understanding math and physics are intimately linked and fundamentally the same! Indeed, I claim that physics is cognitively basic to quantitative science in all domains!!”
=====

I think this is more true today in that a deep understanding of mathematics and its relationship to physics is not felt to be necessary. Most approaches to developing an understanding of physics separate learning from the mathematical language designed to encode it. This division does a disservice to both. When one is seen in the context of the other a deeper understanding of both is developed.

In many ways the mathematics of physics is a formalization of the operations of the mind and so to understand this mathematics is to understand how the mind forms and transforms concepts.

But the problem is I believe much deeper. The most obvious one is that the standard approach has focused on content and ignores the mental tools that are necessary to facilitate its learning.

To be clear, these tools are not mathematical in any sense of that word, just as the hammer and saws that are used to construct a house are not part of the house. These tools are not physical but conceptual because they are utilized in building concepts. These tools are necessary because it is the learner that has to build their own ideas and the more sophisticated the tools the better the understanding.

I would like to claim that the need to change is critical, as today’s students are flat screened. Their world is limited to TV, video games and texting on cell phones.

On another front, we are developing a series of activities to interest grade 5 to 8 students in science. If anyone has any experience in dealing with these students I would be very interested in your experiences.

Please communicate with me directly.

cheers
Rob

[…]

David Hestenes wrote in 2012: The main problem with math education is that the link to physical intuition (the empirical source of mathematical ideas) is seriously degraded, if not broken altogether. Mathematical understanding requires development of both physical and mathematical intuition, which supply the essential repertoire of mental structures for constructing math meaning.

Physical intuition is cognitively basic, because it supplies the structural link to bodily experience, from which all meaning derives. The fabric of meaning is woven thread by thread from bodily experience and embroidered with metaphor.

George Lakoff claims: Contemporary cognitive science provides empirical grounds for a revolutionary Science of Mind, asserting:
(a) cognition is grounded in the bodily experience,
(b) cognitive processes are mostly unconscious,
(c) spatial-temporal perception and cognition is extended by metaphors
to structure other cognitive domains.

References:
Metaphors We Live By (1980, with Mark Johnson)
Women, Fire and Dangerous Things: what
categories reveal about the mind (1987)
Philosophy in the Flesh (1999, with Mark Johnson)
Where mathematics comes from (2000, with Rafel Núñez)

[…]

Yesterday, Jackie Kane, a long-time modeler in Ohio, suggested PUM (Physics Union Mathematics, by Eugenia Etkina at Rutgers . PUM is “a physics/physical science curriculum that strongly links middle and high school physics curricula and builds on the intrinsic mathematical reasoning to develop and strengthen students’ mathematical concepts at the pre-algebra, algebra and algebra 2 levels.”

David Hestenes lauds PUM as very well thought out.

In regards to PUM, Frank Noschese, an expert modeler in New York state, wrote,
… “Eugenia Etkina‘s COLLEGE PHYSICS text gets a step closer to my iBook vision. The text incorporates her work with video experiments in her ISLE and Physics Union Mathematics [PUM] curricula. In the text, there are QR codes which link to videos of the experiments to be analyzed.”
—————————
Here are relevant URLs, in case you want to explore PUM and ISLE.
pum.rutgers.edu/
www.islephysics.net/ ISLE is college-level (and advanced high school).
paer.rutgers.edu/pt3/ Physics Teaching Technology Resource (200 virtual labs in modeling cycles).

ISLE and PUM are super-compatible with Modeling Instruction. We recommend Eugenia’s physics education research (PER) group as the best group nationwide for modelers who want to earn a Ph.D.

[…]

From: Rob MacDuff <macduff@mac.com>
Subject: A need for change? </macduff@mac.com>

From the responses, it seems that I am not the only one that has issues with the integration of math and physics. But “PUM: Physics Union Mathematics — an outstanding curriculum for high school & middle school”, from my perspective, does not even come close to dealing with the math/science integration problem. However, to give credit where credit is due, they do have a number of very interesting activities. Where I differ is in how they think about the nature of knowledge acquisition.

Here is the issue as I see it. I do not believe that anyone would disagree that 6=3×2 or y = nx, where y, n and x refer to numbers are valid mathematical expression. So if one writes down F=ma, how is this in anyway connected to either 6 = 3×2 or y = nx? If one ponders this for a moment, one quickly comes to realize that there is nothing, not even the symbols = and x. Not only that but numbers themselves remain completely undefined in mathematics (and no, numbers are not abstractions of quantity) whereas F, m and a have definite meanings in physics.

Math deals with axioms and theorems where physics deals with definitions and a somewhat different set of axioms as a means of encoding empirically familiar regularities.

I would like to claim that changing students concepts of mathematics so they work with physics requires at least a minimum of two to three weeks of instruction. The math in mathematics is computational, the math in physics is descriptive.

cheers
Rob

[…]

Notes for a Modeling Theory of Science, Cognition and Instruction
David Hestenes, Arizona State University
Proceedings of the 2006 GIREP conference: Modelling in Physics and Physics Education
download at http://modeling.asu.edu/R&E/Research.html

(excerpt: page 25) Cognitive processes in theoretical physics and mathematics are fundamentally the same, centered on construction and analysis of conceptual models. Semantics plays a far more significant role in mathematical thinking (and human reasoning in general) than commonly recognized — it is the cognitive semantics of mental models, mostly residing in the cognitive unconscious, but often manifested in pattern recognition and construction skills [31].

Mathematical intuition (like physical intuition) is a repertoire of mental structures (schemas) for making and manipulating mental models! This goes a long way toward answering the question: What does it mean to understand a scientific concept?

I am not alone in my opinion on the intimate relation between physics and mathematics. Here is a brief extract from a long diatribe On Teaching Mathematics by the distinguished Russian mathematician V. I. Arnold [32]:

“Mathematics is a part of physics. Physics is an experimental science, a part of natural science. Mathematics is the part of physics where experiments are cheap. . . . In the middle of the 20th century it was attempted to divide physics and mathematics. The consequences turned out to be catastrophic. Whole generations of mathematicians grew up without knowing half of their science and, of course in total ignorance of other sciences.”

Arnold is deliberately provocative but not flippant. He raises a very important educational issue that deserves mention quite apart from the deep connection to cognitive science that most concerns us here.

There is abundant evidence to support Arnold’s claim. For example, up until World War II physics was a required minor for mathematics majors in US universities. Since it was dropped, the mathematics curriculum has become increasingly irrelevant to physics majors, and physics departments provide most of the mathematics their students need. At the same time, mathematicians have contributed less and less to physics, with some exceptions like the Russian tradition that Arnold comes from, which has sustained a connection to physics.

But the most serious consequence of the divorce of mathematics from physics is the fact that, in the U.S. at least, most high school math teachers have little insight into relations of math they teach to science in general and physics in particular.

This chasm between math and science, now fully ensconced in the teachers, may be the single most serious barrier to significant secondary science education reform.

[31] P. Ross (2006), The Expert Mind, Scientific American 295: 64-71.
[32] V. I. Arnold (1997), On Teaching Mathematics,
(http://pauli-uni-muester.de/~munsteg/arnold.html)

[…]

Date: Tue, 25 Jun 2019 20:51:56 +0000
From: Jim Smith <nitac14b@yahoo.com>
Subject: Geometric Algebra (GA) and the discussion of the physics/math linkage</nitac14b@yahoo.com>

Although I haven’t followed the discussion closely, I’ve read enough of it to recognize that the concerns expressed here need to be addressed explicitly by developers of pedagogies, technologies, and materials for teaching GA. Otherwise, GA may become–in students’ minds–just another flavor of the same abstract symbols whose connection to reality has never been apparent.

Participants in this listserv can help GA avoid that fate by critiquing the materials and viewpoints that are posted at the LinkedIn group “Pre-University Geometric Algebra” ( https://www.linkedin.com/groups/8278281/ ). I will be grateful personally for comments on my documents “Learning Geometric Algebra by Modeling Motions of the Earth and Shadows of Gnomons to Predict Solar Azimuths and Altitudes” ( http://vixra.org/pdf/1804.0363v1.pdf ) and “Via Geometric Algebra: Direction and Distance Between Two Points on a Spherical Earth” ( http://vixra.org/pdf/1906.0404v1.pdf ). Both documents address (but insufficiently, as I now realize) the need to connect math with physical reality.

[…]

Date: Wed, 26 Jun 2019 11:56:49 -0700
From: Rob MacDuff <macduff@mac.com>
Subject: Are you sure you are in the right church?</macduff@mac.com>

Jim Smith wrote:
> Although I haven’t followed the discussion closely, I’ve read enough of it to recognize that the concerns expressed here need to be addressed explicitly by developers of pedagogies, technologies, and materials for teaching GA.

Hi Jim, I would have to say that most posts are either rants or pontifications rather than discussions. Discussions require the desire and willingness to ask questions and carry on a dialogue. NOT “how dare you pose questions”!

Read what follows and tell me if you don’t think that your posting is totally weird as my plan yesterday was to post the following:

Why is this algorithmic/computational approach to learning so difficult for students? Let me provide a simple example from GA. Suppose that you draw two vectors and label them a and b. What Hamilton tried to do and what Gibbs and Heaviside totally screwed up (vector algebra – talk about if the math works it must be true – how utterly inane: multiply two vectors and get either a scalar or a vector??? sheesh!) was to describe one vector in terms of the other. David Hestenes improved it dramatically and called it GA. This is my version of GA which is slightly different from David’s.
An algorithmic/computational approach to GA
a = a easy to follow
a = a1 again easy to follow
a = a (bb/bb) not so easy to follow
a = (ab/bb) a impossible to follow. Even though this has to be true, the reaction is generally of the form EEEEEK followed by running for the hills.

My point is this, when and if you write F/a =m or v = d/t, you are going to create the exact same response in your students, it certainly did in my mind when I first encountered it.

BTW Jim, I taught GA to a home schooled 13 year old who had already taken CIMM. No problem at all, he loved it.

> Otherwise, GA may become–in students’ minds–just another flavor of the same abstract symbols whose connection to reality has never been apparent.

Unfortunately Jim, your words are not “speaking to the choir”. It is really hard and maybe impossible to really understand GA by discussing ab as a geometric product, this will work if your b’s are only ever unit vectors which in general are not the case. i.e. ab = a*b + a^b only equals (ab) b if b is a unit vector (in other words bb=1) however, a always equal ((a*b)/(bb) + (a^b)/(bb)) b

The potential descriptive relationship nature of (ab/bb) is essential as it is the essence of David’s geometric thinking.

cheers
Rob

[…]

Date: Thu, 27 Jun 2019 07:00:02 +0000
From: Jane Jackson <jane.jackson@asu.edu>
Subject: Re: David Hestenes on the divorce of math from physics in the structure of the K-12 curriculum</jane.jackson@asu.edu>

(I re-send, because ASU’s security software garbled the URL.]

Regarding the divorce of math from physics in the structure of the K-12 curriculum (my original focus, in my post on June 20).
A partial solution is Geometric Algebra. David Hestenes developed geometric algebra (GA) to UNIFY math and physics. GA is a unified mathematical language for ALL of physics. It is very powerful! It is used in the space program for satellite tracking, in robotics, in crystallography, computer vision, general relativity, and much more! Dr. Hestenes gives keynote addresses at international conferences on GA; a recent GA conference was dedicated to him.

GA can be a central focus of high school geometry courses. David Hestenes sees formal proofs as poor course content. He has a vision of a more effective geometry course, centered on GA. To see David Hestenes’ vision, read the prologue (below) to his Primer on Geometric Algebra for introductory mathematics and physics. (He used it at his full-day workshops at ASU in summer for teachers, and at AAPT summer meetings.

Last summer’s graduate course at ASU, PHS 542: Integrated Math and Physics, featured GA. You can download the PHS 542 theory and homework in 2018 at modeling.asu.edu/MNS/MNS.html .Also, a picture of David Hestenes and Geoff Clarion in PHS542 in 2018. — Jane Jackson

David Hestenes wrote (at geocalc.clas.asu.edu/html/IntroPrimerGeometricAlgebra.html ) :
————————–
Physics teachers are universally dismayed by the paltry understanding of mathematics that students bring from their mathematics courses. Blame is usually laid on faulty teaching. But I hold that the crux of the problem is deeply embedded in the curriculum. From the perspective of a practicing scientist, the mathematics taught in high school and college is fragmented, out of date and inefficient!

The central problem is found in high school geometry. Many schools are dropping the course as irrelevant. But that would be a terrible mistake for reasons already clear to Galileo at the dawn of science.
* Geometry is the starting place for physical science, the foundation for mathematical modeling in physics and engineering and for the science of measurement in the real world.
* Synthetic methods employed in the standard geometry course are centuries out of date; they are computationally and conceptually inferior to modern methods of analytic geometry, so they are only of marginal interest in real world applications.
* A reformulation of Euclidean geometry with modern vector methods centered on kinematics of particle and rigid body motions will simplify theorems and proofs, and vastly increase applicability to physics and engineering.

A basic pedagogical principle: The depth and extent of student learning is critically dependent on the quality of the available mathematical tools.

Therefore, we can expect a well-designed curriculum based on vector methods to produce significant improvements in the depth, breadth, and usefulness of student learning. Further enhancements can be expected from software that facilitates application of vector methods.
——————————
References for further study:
D. Hestenes, “Oersted Medal Lecture 2002: Reforming the mathematical language of physics, “ Am. J. Phys. 71: 104-121 (2003).
D. Hestenes, New Foundations for Classical Mechanics (Kluwer, Dordrecht, 1986, 2nd ed. 1999)
Both are at David Hestenes’ website, at this URL: geocalc.clas.asu.edu

[…]

Date: Mon, 1 Jul 2019 06:19:42 +0000
From: Jane Jackson <jane.jackson@asu.edu>
Subject: Why is important to take multiple Modeling Workshops? by David Hestenes</jane.jackson@asu.edu>

[Why is important to take multiple Modeling Workshops? David Hestenes addressed this question, repeatedly. — Jane Jackson]

CULTIVATION OF TEACHING EXPERTISE, by David Hestenes (1995)

What does it take to become a master teacher like Malcolm Wells? The skill and training required for expert teaching are generally underestimated and undervalued. Accolades and awards for teaching are often based on superficial criteria. Malcolm’s example sets a higher standard – one to be emulated if teaching is to be elevated.

An extensive review and analysis of the literature on expert performance has identified essential conditions for the acquisition of expert skill in most domains. The chief condition is prolonged effort to improve performance extending for a minimum of 10 years. A striking conclusion of the study is that individual differences, even among elite performers, are primarily due to intense practice rather than innate talent. Music, sports, chess, scientific research and literature are among the several domains examined in the study. Teaching was not included, of course, but there is no reason to doubt that the general conditions for acquisition of expertise apply there as well. Assuming so, we can draw some important conclusions about the professional development of teachers.

Our first conclusion is that standard teacher preparation and in-service teaching experience is not sufficient to develop a high level of teaching expertise. Consider what is involved. Even assuming that a physics teacher has acquired adequate “content knowledge” from a B.A. or even an M.A. in physics, the relevant pedagogical training is practically nil. After landing a teaching position, the tyro teacher may scramble for a couple of years to organize lab materials and activities, problem sets and homework, grading procedures and the rest into a smoothly running course. By this time the teacher has adopted a personal style and a teaching routine which makes it possible to cope with the perpetual exigencies of everyday teaching.

Most physics teachers are dedicated to their job and care deeply about their students. But caring and dedication are not enough! The experience of routine teaching over many years, even when conducted with dedication and enthusiasm, will not contribute significantly to the development of teaching expertise – just as plug-and-chug practice does little to promote problem solving skill! … Most teachers become trapped in a routine that prevents them from coming close to realizing their true potential.

How to rise above it!?

First consider how Malcolm [Wells] did it. The schools have so crowded the teacher’s daily schedule that no room is left for cultivating expertise. Malcolm, of course, did it on his own time – evenings, weekends, vacations – routinely working into the small hours of the morning. For Malcolm, teaching is a calling, not just a job. He was unrelenting in his efforts to improve – continuously monitoring the progress of his students, revising assignment and activities, designing and building new apparatus, always on the lookout for some other teacher’s good idea.

Malcolm is a counter example to the myth of the “born teacher.” Unlike the typical award-winning teacher, Malcolm is not a master showman. Rather, he goes out of his way to give the students center stage. …

Few can match the prolonged and dedicated effort of Malcolm Wells, but many can aspire to his level of teaching expertise, because Malcolm has prepared the way. …

To develop a practical means for training teachers in the modeling method, we joined Malcolm in designing and conducting a series of NSF summer workshops for in-service teachers. …

… To reach and maintain his/her full potential, the teacher must be engaged in lifelong professional development. It will take at least ten years to reach the teacher’s highest level of competence. Mere accumulation of academic credits and hours of classroom teaching count for little, unless the teacher is consistently engaged in deliberate effort to improve.

from the 1995 AJP paper: A modeling method for high school physics instruction, by Malcolm Wells, David Hestenes, & Gregg Swackhamer. Download at modeling.asu.edu . Click on “Research and Evaluation”.

[…]

There are 2 messages totaling 87 lines in this issue.

Topics of the day:

1. MODELING Digest – 5 Jul 2019 to 7 Jul 2019 (#2019-137)
2. Recent Research on Multiple Representations

—————————
To unsubscribe: listserv@asu.edu. In the body, type this: signoff modeling. If that doesn’t work: jane.jackson@asu.edu
—————————

Date: Mon, 8 Jul 2019 08:30:03 -0500
From: John Clement <clement@hal-pc.org>
Subject: Re: MODELING Digest – 5 Jul 2019 to 7 Jul 2019 (#2019-137)</clement@hal-pc.org>

There is a study which thoroughly debunked learning styles. The study first categoirizedt the students “learning styles”, then they gave two lessons using opposite learning styles, visual or aural. The results on the followup tests showed that there was no increase in learning when the style matched the teaching method. Both style groups learned the same amount irrespective of the method.

There is evidence from dyslexia research that having students use kinesthetic, aural, and visual feedback simultaneously does help them. The Orton-Gillingham method uses this.

Learning styles is what I would categorize as pop psychology with no strong controlled research supporting the supposition that it can be used to improve learning. The method of communicating concepts should be coupled to the concept, not the learner, with strong active engagement of the learner in the process. Yet I think schools still tend to push it.

There are factors which in a sense relate to learning styles, but are actually disabilities. I have always had a problem with being able to decode audible speech. Sometimes it comes out as gibberish. This is not a style, but rather a slight disability. So presenting something both aurally and visually in a quiet settin can benefit the few students who have a disability. But having the students actively work at learning through research based activities is the real key. Presentation would be the initial phase, or concrete preparation for a given activity. Notice that multiple representations is analogous to the Orton-Gillingham method which also uses multiple representations simultanesously.

John M. Clement

—————————————————————————————–
[Interesting research. What DOES matter are multiple representations and whiteboarding. (Do you see a connection between multiple representations and “perceived learning styles”? I’ve never read anything connecting the two ideas, but it seems to me that “learning styles” are a poor (i.e., naive) way of conceiving representations of models. What do you think? — Jane J)

The Problem with “Learning Styles”
by Cindi May (May 29, 2018)
Scientific American
www.scientificamerican.com/article/the-problem-with-learning-styles/

Two excerpts:
A recent review* of the scientific literature on learning styles found scant evidence to clearly support the idea that outcomes are best when instructional techniques align with individuals’ learning styles. In fact, there are several studies that contradict this belief. It is clear that people have a strong sense of their own learning preferences (e.g., visual, kinesthetic, intuitive), but it is less clear that these preferences matter.
…
[A recent research study of 400 students in a college anatomy course showed that] most students are not employing study strategies that mesh with self-reported learning preferences, and the minority who do show no academic benefit.

*URL: journals.sagepub.com/doi/full/10.1111/j.1539-6053.2009.01038.x
Learning Styles: Concepts and Evidence
by Harold Pashler, Mark McDaniel, Doug Rohrer (2009).
Psychological Science in the Public Interest 9 (3), 105-119.
I quote them: “Although the literature on learning styles is enormous, very few studies have even used an experimental methodology capable of testing the validity of learning styles applied to education. Moreover, of those that did use an appropriate method, several found results that flatly contradict the popular meshing hypothesis.
We conclude therefore, that at present, there is no adequate evidence base to justify incorporating learning-styles assessments into general educational practice.”

[…]

Date: Tue, 9 Jul 2019 06:56:08 +0000
From: Jane Jackson <jane.jackson@asu.edu>
Subject: Recent Research on Multiple Representations</jane.jackson@asu.edu>

You might like to read “An Overview of Recent Research on Multiple Representations” by David Rosengrant, Eugenia Etkina, and Alan Van Heuvelen. I downloaded it for free at this URL (I did a google search):
www.researchgate.net/publication/237623500_An_Overview_of_Recent_Research_on_Multiple_Representations

They begin by citing Brant Hinrich’s paper on system schema (which you can freely download at the ASU modeling legacy website: modeling.asu edu . Click on “resources for the modeling classroom”.

An excerpt of their own research:

“The research by Rosengrant, Etkina and Van Heuvelen and by DeLeone and Gire shows that if students learn physics in an environment that emphasized the use multiple representations, students will use them to help solve problems. Does the use of these different representations improve problem-solving performance?

DeLeone and Gire [8] found that those students who successfully solved 3 or more of the 5 coded problems were all high MR users. They drew a picture, an extended force diagram, an energy system diagram, or plotted a graph. On 4 out of those 5 problems students who used representations other than mathematical had a higher success rate than those who did not.”

Several other insights from physics ed research are included. A fascinating paper!

— Jane Jackson, ASU

[…]

End of MODELING Digest – 7 Jul 2019 to 9 Jul 2019 (#2019-138)
*************************************************************

There are 5 messages totaling 226 lines in this issue.

Topics of the day:

1. MODELING Digest – 19 Jul 2019 to 22 Jul 2019 (#2019-146) (2)
2. Searching for Physics Education Research Participants (specifically
teachers of IB)
3. One perspective on the learning theory
4. Modeling and learning theory

—————————
To unsubscribe: listserv@asu.edu. In the body, type this: signoff modeling. If that doesn’t work: jane.jackson@asu.edu
—————————

Date: Tue, 23 Jul 2019 15:15:44 +0500
From: Nathan Belcher <contactnathanbelcher@gmail.com>
Subject: Re: MODELING Digest – 19 Jul 2019 to 22 Jul 2019 (#2019-146)</contactnathanbelcher@gmail.com>

James,

Modeling Instruction’s foundation comes from Dr. Hestenes; he created a theory known as the Modeling Theory of Cognition. This theory posits that humans construct “mental models,” which we are constantly creating, refining, and applying. When humans share the models to predict or explain a part of the world, mental are elevated to “conceptual models.” We then test the “conceptual models” for agreement or disagreement with data from experiments, then reject, refine, or accept the “conceptual model”—until further experiments provide more data about the “conceptual model.”

The Modeling Theory of Cognition uses the ideas of Constructivism* but focuses the construction of information into models, leading to the learning cycle in Modeling Instruction. Students are collect or are given data for a particular topic; from there, students organize the information into their initial mental model. Through discussion and application, students refine their mental model to account for new information. If the information cannot be adequately explained by the refined model, students begin the process again.

[* I used the definition of Constructivism from this article: https://lidtfoundations.pressbooks.com/chapter/behaviorism-cognitivism-constructivism/.]

If you would like more information on the Modeling Theory of Cognition, I have compiled information from several of Dr. Hestenes’ papers into a short article. The information was a part of my dissertation—Modeling Instruction in AP Physics C. Here is a link to the article: https://www.nathantbelcher.com/modeling-instruction (scroll to the bottom for the .pdf).

If anyone would like to discuss further, feel free to respond here or contact me off-list.

All the best.

Nathan Belcher, Ed.D.
Singapore American School
Contactnathanbelcher@gmail.com
—————————
To unsubscribe: listserv@asu.edu. In the body, type this: signoff modeling. If that doesn’t work: jane.jackson@asu.edu
—————————

Date: Tue, 23 Jul 2019 10:55:00 -0700
From: Nathaniel Lohmann <nathaniel.lohmann@gmail.com>
Subject: Searching for Physics Education Research Participants (specifically teachers of IB)</nathaniel.lohmann@gmail.com>

Teachers Tammy Draughon (Temecula, CA) and Nathaniel Lohmann (Colorado Springs, CO), in partial fulfillment of the MNS degree at Arizona State, are searching for teachers and students willing to participate in our action research project. Our research focuses on links between student grit and student performance/confidence, specifically for students enrolled in advanced high school physics classes (i.e. IB and AP). While we have many AP teachers already participating, we are in need of several more IB Physics classes (SL or HL) to have a legitimate sample size.

Teachers and students participating in our research are asked to collect and submit data for two inventories, the FCI and a mindset/grit inventory, each taken before and after the mechanics unit. Both of these inventories can be taken securely online or with pencil and paper. The FCI must be taken during class time (per AMTA regulation), but the mindset/grit survey can be completed by the students outside of class. Collected data can be forwarded to the teacher if requested. If you are interested in participating, or if you have any additional questions, please contact Nathaniel Lohmann at nathaniel.lohmann@d11.org.

Thank you!

Tammy Draughon
Temecula, CA.

Nathaniel Lohmann
Colorado Springs, CO.

—————————
To unsubscribe: listserv@asu.edu. In the body, type this: signoff modeling. If that doesn’t work: jane.jackson@asu.edu
—————————

Date: Tue, 23 Jul 2019 12:07:24 -0700
From: Rob MacDuff <macduff@mac.com>
Subject: One perspective on the learning theory</macduff@mac.com>

James Kerr asked:
> Is modeling instruction based on learning theory?

No. It is based upon a theory of knowledge. i.e. our knowledge of the world consists of models.
The fact that Socratic questioning aids model construction doesn’t constitute a theory.

> Is modeling instructional theory a combination of Cognitivism and Constructivism and Connectivism?

I would not put behaviorism, followed by cognitivism, followed by constructivism and followed by connectivism in the category of theories. They are more belief structures, as in: “humans construct their own knowledge.” Let’s force them to construct knowledge by asking questions for which they have absolutely no way of knowing the answer. Oh, look they have this misconception! The kid guesses and s/he is now labeled. But seriously, does the answer not indicate a missing conception? See McDermott’s work to study how removing misconceptions leads to “correct” conceptions.

It is my opinion that these beliefs have done vastly more harm to educational practice than aid. Modeling instruction is by far the most useful at the moment.

A theory of learning should have the following aspects to it. It should:
1/ specify the mental tools necessary for constructing concepts.
2/ characterize knowledge as systems.
3/ specify the system components that form the knowledge structures.
4/ define thinking in terms of mental processing that are tied to the mental tools.
5/ specify how the knowledge structures are utilized in reasoning.
6/ define the role of these four representational systems, linguistic, algebraic, diagrammatic, and graphic having in increasing the level of comprehension.
7/ how understanding is associated with the coordination of the activation of the various regions of the brain.

And why do you ask?

cheers
Rob

—————

There are 5 messages totaling 226 lines in this issue.

Topics of the day:

—————————
To unsubscribe: listserv@asu.edu. In the body, type this: signoff modeling. If that doesn’t work: jane.jackson@asu.edu
—————————

Date: Tue, 23 Jul 2019 15:15:44 +0500
From: Nathan Belcher <contactnathanbelcher@gmail.com>
Subject: Re: MODELING Digest – 19 Jul 2019 to 22 Jul 2019 (#2019-146)</contactnathanbelcher@gmail.com>

James,

[* I used the definition of Constructivism from this article: https://lidtfoundations.pressbooks.com/chapter/behaviorism-cognitivism-constructivism/.]

If anyone would like to discuss further, feel free to respond here or contact me off-list.

All the best.

Thank you!

Tammy Draughon

Temecula, CA

Nathaniel Lohmann

Colorado Springs, CO

—————————
To unsubscribe: listserv@asu.edu. In the body, type this: signoff modeling. If that doesn’t work: jane.jackson@asu.edu
—————————

Date: Tue, 23 Jul 2019 12:07:24 -0700
From: Rob MacDuff <macduff@mac.com>
Subject: One perspective on the learning theory</macduff@mac.com>

James Kerr asked:
> Is modeling instruction based on learning theory?

No. It is based upon a theory of knowledge. i.e. our knowledge of the world consists of models.
The fact that Socratic questioning aids model construction doesn’t constitute a theory.

> Is modeling instructional theory a combination of Cognitivism and Constructivism and Connectivism?

It is my opinion that these beliefs have done vastly more harm to educational practice than aid. Modeling instruction is by far the most useful at the moment.

And why do you ask?

cheers

Rob

—————————
To unsubscribe: listserv@asu.edu. In the body, type this: signoff modeling. If that doesn’t work: jane.jackson@asu.edu
—————————

Date: Tue, 23 Jul 2019 20:25:23 +0000
From: “Cabot, Nick” <nick.cabot@oregonstate.edu>
Subject: Re: MODELING Digest – 19 Jul 2019 to 22 Jul 2019 (#2019-146)</nick.cabot@oregonstate.edu>

A complete elucidation of the conceptual underpinnings of modeling instruction can be found in Ibrahim Halloun’s book Modeling Theory in Science Education. Ibrahim was a student and collaborator of David’s at ASU and did much of the early work in developing the theory behind modeling pedagogy (along with Malcolm Wells, Gregg Swackhamer, Jane Jackson, and others). Put most simply, modeling instruction is decidedly a constructivist theory of learning – the whole point of the pedagogy is to help students construct (basic) conceptual models in science – since that is, in fact, how science is done.

The theory is that humans naturally and unconsciously develop mental models of their experiences as predictive devices (we learn by doing and remembering – what happened before should happen again in more or less the same way) and also, but to a much lesser extent, as explanatory devices. These mental models are primitive (unsophisticated), limited – by both a lack of perceptual acuity and by narrow experience, not particularly well thought out – if at all, and always incomplete, if not just plain wrong. But, with a modeling teacher’s guidance, this prior knowledge can be transformed into rigorous conceptual models via structured experiences requiring evidence-based explanations. Modeling instruction provides a venue for students to collaboratively co-construct their conceptual understanding of key models that are embedded in well established theories of science.

Nick Cabot

——————–

Date: Mon, 22 Jul 2019 08:07:56 -0400
From: James Kerr <wauseondowntown@gmail.com>
Subject: Learning Theory</wauseondowntown@gmail.com>

Is modeling instruction based on learning theory? Is modeling instructional
theory a combination of Cognitivism and Constructivism and Connectivism?
Is modeling instruction in science considered as its own learning theory?
Thank you for your feedback.

—————————
To unsubscribe: listserv@asu.edu. In the body, type this: signoff modeling. If that doesn’t work: jane.jackson@asu.edu
—————————

Date: Tue, 23 Jul 2019 14:39:29 -0700
From: Colleen Megowan-Romanowicz PhD <colleen@modelinginstruction.org> Subject: Modeling and learning theory</colleen@modelinginstruction.org>

In 2006 David Hestenes wrote a paper entitled Notes on a Modeling Theory of Science Cognition and Instruction. Here is the abstract: “Modeling Theory provides common ground for interdisciplinary research in science education and the many branches of cognitive science, with implications for scientific practice, instructional design, and connections between science, mathematics and common sense.”

The development of the Modeling Method of Instruction over the past 35 has both drawn upon and informed the development of this theory, which reflects the most current theories of both cognition and the learning sciences.

This paper provides an accessible look at both the theoretical underpinnings of Modeling and the history of how it came to be.

If you would like me to send you a copy please drop me a note off-list.

Colleen
Colleen Megowan-Romanowicz PhD
Senior Fellow, American Modeling Teachers Association
colleen@modelinginstruction.org | http://modelinginstruction.org

*****************************
Is modeling instruction based on learning theory? Is modeling instructional theory a combination of Cognitivism and Constructivism and Connectivism?
Is modeling instruction in science considered as its own learning theory?
Thank you for your feedback.

—————————
To unsubscribe: listserv@asu.edu. In the body, type this: signoff modeling. If that doesn’t work: jane.jackson@asu.edu
—————————

End of MODELING Digest – 22 Jul 2019 to 23 Jul 2019 (#2019-147)
***************************************************************

Date: Tue, 23 Jul 2019 20:25:23 +0000
From: “Cabot, Nick” <nick.cabot@oregonstate.edu>
Subject: Re: MODELING Digest – 19 Jul 2019 to 22 Jul 2019 (#2019-146)</nick.cabot@oregonstate.edu>

Nick Cabot
———————–

Date: Mon, 22 Jul 2019 08:07:56 -0400
From: James Kerr <wauseondowntown@gmail.com>
Subject: Learning Theory</wauseondowntown@gmail.com>

—————————
To unsubscribe: listserv@asu.edu. In the body, type this: signoff modeling. If that doesn’t work: jane.jackson@asu.edu
—————————

Date: Tue, 23 Jul 2019 14:39:29 -0700
From: Colleen Megowan-Romanowicz PhD <colleen@modelinginstruction.org> Subject: Modeling and learning theory</colleen@modelinginstruction.org>

In 2006 David Hestenes wrote a paper entitled Notes on a Modeling Theory of Science Cognition and Instruction. Here is the abstract: “Modeling Theory provides common ground for interdisciplinary
research in science education and the many branches of cognitive science, with implications for scientific practice, instructional design, and connections between science, mathematics and common sense.”

This paper provides an accessible look at both the theoretical underpinnings of Modeling and the history of how it came to be.

If you would like me to send you a copy please drop me a note off-list.

Colleen
Colleen Megowan-Romanowicz PhD
Senior Fellow, American Modeling Teachers Association
colleen@modelinginstruction.org | http://modelinginstruction.org

—————————
To unsubscribe: listserv@asu.edu. In the body, type this: signoff modeling. If that doesn’t work: jane.jackson@asu.edu
—————————

There is 1 message totaling 99 lines in this issue.

Topics of the day:

1. Modeling and learning theory

—————————
To unsubscribe: listserv@asu.edu. In the body, type this: signoff modeling. If that doesn’t work: jane.jackson@asu.edu
—————————

Date: Sun, 28 Jul 2019 06:39:29 +0000
From: Jane Jackson <jane.jackson@asu.edu>
Subject: Re: Modeling and learning theory</jane.jackson@asu.edu>

Last Tuesday, Colleen Megowan posted:
————————
“In 2006 David Hestenes wrote a paper entitled Notes on a Modeling Theory of Science Cognition and Instruction. Here is the abstract: “Modeling Theory provides common ground for interdisciplinary research in science education and the many branches of cognitive science, with implications for scientific practice, instructional design, and connections between science, mathematics and common sense.”

The development of the Modeling Method of Instruction over the past 35 [years]has both drawn upon and informed the development of this theory, which reflects the most current theories of both cognition and the learning sciences.

This paper provides an accessible look at both the theoretical underpinnings of Modeling and the history of how it came to be.
———————
You can download David Hestenes’ article “Notes for a Modeling Theory …” (2006) at
modeling.asu.edu/R&E/Research.html . I find this article, and ALL of David Hestenes’ writings, insightful!

I quote from it:
—————————–
Insights into student thinking … are insufficient for promoting a transition to Newtonian thinking in the classroom. The literature is replete with attempts to address specific misconceptions with partial success at best. So what accounts for the singular success of Modeling Instruction as measured by the FCI? As for any expert performance, detailed planning and preparation is essential for superior classroom instruction. (The intensive Modeling Workshops help teachers with that.) However, Modeling Instruction is unique in its strategic design.

Rather than address student misconceptions directly, Modeling Instruction creates an environment of activities and discourse to stimulate reflective thinking about physical phenomena that are likely to evoke those misconceptions. The environment is structured by an emphasis on models and modeling with multiple representations (maps, graphs, diagrams, equations). This provides students with conceptual tools to sharpen their thinking and gives them access to Newtonian concepts. In this environment students are able to adjust their thinking to resolve discrepancies within the Newtonian system, which gradually becomes their own. Rather than learning Newtonian concepts piecemeal, they learn them as part of a coherent Newtonian system.

Construction of a Newtonian model requires coordinated use of all the Newtonian concepts, and only this reveals the coherence of the Newtonian system. That coherence is not at all obvious from the standard statement of Newton’s Laws. I believe that learning Newtonian concepts as a coherent system best accounts for high FCI scores. Logically this is only a sufficient condition for a high score, but I estimate that a high score from piecemeal understanding of Newtonian physics is improbably low. Thus, it is best to interpret overall FCI score as a measure of coherence in understanding Newtonian physics.
—————————-

peace,
Jane Jackson, Co-Director, ASU Modeling Instruction Prgm
Box 871504, Dept.of Physics, ASU, Tempe, AZ 85287
480-965-8438/480-314-1522. The URL is modeling.asu.edu
Jane.Jackson@asu.edu I care. Do you?

________________________________
From: modeling – teachers discuss Modeling Instruction in physics <modeling@asu.edu> on behalf of Colleen Megowan-Romanowicz PhD <colleen@modelinginstruction.org> Sent: Tuesday, July 23, 2019 2:39 PM
To: MODELING@ASU.EDU <modeling@asu.edu>
Subject: [PHYSICS_M] Modeling and learning theory</modeling@asu.edu></colleen@modelinginstruction.org></modeling@asu.edu>

In 2006 David Hestenes wrote a paper entitled Notes on a Modeling Theory of Science Cognition and Instruction. Here is the abstract: “Modeling Theory provides common ground for interdisciplinary
research in science education and the many branches of cognitive science, with implications for scientific practice, instructional design, and connections between science, mathematics and common sense.”

This paper provides an accessible look at both the theoretical underpinnings of Modeling and the history of how it came to be.

—————————
To unsubscribe: listserv@asu.edu. In the body, type this: signoff modeling. If that doesn’t work: jane.jackson@asu.edu
—————————

End of MODELING Digest – 23 Jul 2019 to 27 Jul 2019 (#2019-148)
***************************************************************

///////

Knowledge Management Research Group

1 thought on “Physics and its Models”

Leave a Reply Cancel reply