This page is a sub-page of our page on Hyperbolic Geometry.
///////
Related KMR-pages:
• The Beltrami-Klein model
• Elliptic Geometry
• Euclidean Geometry
• Non-Euclidean Geometry
• Projective Geometry
• Projective Metrics
• The Euclidean Degeneration
///////
Books:
• John Stillwell (2016), Elements of Mathematics – From Euclid to Gödel,
Princeton University Press, ISBN 978-0-691-17854-7.
• John Stillwell (1999, (1989)), Mathematics and Its History, Springer, ISBN 0-387-96981-0.
• Jeremy Gray (2007), Worlds Out of Nothing – A Course in the History of Geometry in the 19th Century, Springer, ISBN 1-84628-632-8.
///////
Other related sources of information:
• The Riemann-Poincaré disc model (at Wikipedia)
///////
Representation: [ \, l_{ine} \, ]_{P_{oincaré}M_{odel}} = \left< \, c_{ircleSegment} \, \perp \, a_{bsolute} \, \right>_{P_{oincaré}M_{odel}}
Representation: [ \, a_{bsolute} \, ]_{P_{oincaré}M_{odel}} = \left< \, c_{ircle} \, \right>_{P_{oincaré}M_{odel}}
Representation: [ \, a_{ngle} \, ]_{P_{oincaré}M_{odel}} = [ \, a_{ngle} \, ]_{E_{uclidean}G_{eometry}}
///////
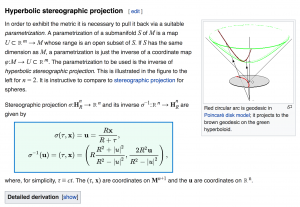
Hyperbolic sterographic projection
(at Wikipedia/Poincaré disk model):
///////
The Riemann-Poincaré model from hyperbolic stereographic projection
(moving point):
The interactive simulation that created this movie.
///////
The Riemann-Poincaré model from hyperbolic stereographic projection (moving point) (rotating around the z-axis):
///////
The Riemann-Poincaré model (Rot Z):
///////
The Riemann-Poincaré model (varying the parameter a):
The interactive simulation that created this movie.
///////
///////
Relating the Riemann-Poincaré model to the Beltrami-Klein model
Projecting the Beltrami-Klein model into the Riemann-Poincaré model
(mediated by the lower vertical semi-circle):
///////
Projecting the Beltrami-Klein model into the inside and outside of the Riemann-Poincaré model (mediated by the full vertical circle):
The interactive simulation that created this movie.
///////
Projecting the Beltrami-Klein model into the Riemann-Poincaré model
(mediated by translating the vertical plane with the lower semi-circle):
///////
Mapping the Beltrami-Klein model to the Riemann-Poincaré model
(pencil on a boundary point):
///////
Mapping the Beltrami-Klein model to the Riemann-Poincaré model
(concentric hypercycles):
The interactive simulation that created this movie.
///////
Devil moving rigidly in the Riemann-Poincaré disc:
///////
Angels and Devils moving rigidly in the Riemann-Poincaré disc:
///////
H.S.M. Coxeter discusses the math behind M.C. Escher’s Circle Limit IV:
///////
Illuminating hyperbolic geometry
(Henry Segerman and Saul Schleimer on YouTube):
///////
Playing Sports in Hyperbolic Space
(Numberphile on Youtube):
///////