Denna sida är en undersida till vår sida om Euclidean Geometry.
///////
Relaterade KMR-sidor:
• Linear Algebra
• The Mathematical Explainatorium
///////
De interaktiva simuleringarna på denna sida kan navigeras med “the Fee Viewer of the Graphing Calculator“.
///////
Representation och Rekonstruktion av en Presentant mot en viss Bakgrund
Representation: \, [ \, p_{resentant} \, ]_{B_{akgrund}} \, \mapsto \, \left< \, r_{epresentant} \, \right>_{B_{akgrund}}
Rekonstruktion: \, \left( \, \left< \, r_{epresentant} \, \right>_{B_{akgrund}} \, \right)_{B_{akgrund}} \mapsto \,\, p_{resentant}
///////
Två vinkelräta linjer genom punkten (0, m) på lutningsform:
\, [ \, l_{inje1} \, ]_{L_{utningsForm}} \, \mapsto \, \left< \; y = kx + m \; \right>_{L_{utningsForm}} .
Denna form kan representera alla linjer i planet utom linjen \, x = 0 \, ,
som motsvarar ett oändligt värde på lutningen \, k .
Den vinkelräta linjen genom punkten (0, m) på lutningsform ges av
\, [ \, l_{inje2} \, ]_{L_{utningsForm}} \, \mapsto \, \left< \; y = (-\frac{1}{k})x + m \; \right>_{L_{utningsForm}} .
Denna form kan representera alla linjer i planet utom linjen \, y = 0 \, ,
som motsvarar ett oändligt värde på lutningen \, k .
Den interaktiva simulering som skapade denna film.
///////
Linje på tvåpunktsform
Denna form kan representera alla linjer i planet.
Låt \, A \, och \, B \, vara två dragbara punkter. En dragbar punkt representeras i Graphing Calculator som ett komplext tal. \, xy -koordinaterna för punkterna \, A \, och \, B \, ges därför av
\, (\mathrm{Re} \, A, \mathrm{Im} \, A) \, respektive \, (\mathrm{Re} \, B, \mathrm{Im} \, B) .
Den interaktiva simulering som skapade denna film.
///////
Två vinkelräta linjer genom origo på vinkelform
Denna form kan representera alla linjer (i planet) som går genom origo.
\, [ \, l_{inje1} \, ]_{V_{inkelForm}} \, \mapsto \, \left< \; (x-a) \sin \phi - (y-b) \cos \phi = 0 \; \right>_{V_{inkelForm}} .
Den vinkelräta linjen genom punkten \, (a, b) \, på vinkelform ges av
\, [ \, l_{inje2} \, ]_{V_{inkelForm}} \, \mapsto \, \left< \; (x-a) \cos \phi + (y-b) \sin \phi = 0 \; \right>_{V_{inkelForm}} .
Den interaktiva simulering som skapade denna film.
///////
Två vinkelräta linjer genom origo på hyperplansform
Den interaktiva simulering som skapade denna film.
///////
Två vinkelräta linjer genom genom punkten \, (a, b) \, på “affinhyperplansform”
Denna form kan representera alla linjer i planet.
TERMINOLOGI: Ett affint hyperplan är ett plan som kan vara parallellförskjutet så att det inte nödvändigtvis går genom origo – vilket ett hyperplan alltid gör.
En dragbar punkt representeras i Graphing Calculator som ett komplext tal.
Inför variablerna \, a = \mathrm{Re} \, A \, och \, b = \mathrm{Im} \, A \, och låt \, A \, vara en dragbar punkt.
\, xy -koordinaterna för punkten \, A \, ges då av \, (A_x, A_y) = (a, b) .
\, [ \, l_{inje1} \, ]_{A_{ffinHyperPlansForm}} \, \mapsto \, \left< \; p (x-a) + q (y-b) = 0 \; \right>_{A_{ffinHyperPlansForm}} .
Den vinkelräta linjen genom punkten \, (a, b) \, ges av:
\, [ \, l_{inje2} \, ]_{A_{ffinHyperPlansForm}} \, \mapsto \, \left< \; q (x-a) - p (y-b) = 0 \; \right>_{A_{ffinHyperPlansForm}} .
Den interaktiva simulering som skapade denna film.
///////
Linje genom punkten (Re A, Im A) vinkelrät mot riktningen (Re B, Im B)
Denna form kan representera alla linjer i planet.
Låt \, A \, och \, B \, vara två dragbara punkter. En dragbar punkt representeras i Graphing Calculator som ett komplext tal. \, xy -koordinaterna för punkterna \, A \, och \, B \, ges av \, (A_x, A_y) = (\mathrm{Re} \, A, \mathrm{Im} \, A) \, respektive \, (B_x, B_y) = (\mathrm{Re} \, B, \mathrm{Im} \, B) .
Den interaktiva simulering som skapade denna film.
///////
Linje genom punkten (Re A, Im A) längs riktningen (Re B, Im B) på parameterform
Denna form kan representera alla linjer i planet.
Den interaktiva simulering som skapade denna film.
///////
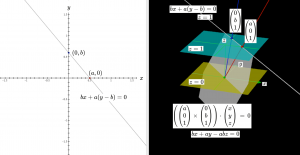
Eulkidiska punkter och linjer i planet uttryckta i homogena koordinater
Det Euklidiska planet kan identifieras med planet \, z = 1 \, i den Euklidiska 3D-rymden.
Den homogena representationsformen kan representera alla Euklidiska punkter och linjer i planet. Dessutom har den exakt det “utrymme” som behövs för att kunna representera ett antal nya punkter (kallade “oändligt avlägsna”). Alla “oändlighetspunkter” har sin \, z -koordinat lika med noll och måste därför ligga på en och samma linje (kallad “linjen i oändligheten“). Denna linje representeras av planet \, z = 0 . Detta leder till så kallad projektiv geometri.
Linjens skärningspunkt med \, x-axeln har \, xy-koordinaterna \, (a,0) .
Linjens skärningspunkt med \, y-axeln har \, xy-koordinaterna \, (0,b) .
Linjens ekvation i det Euklidiska planet ges av \; bx + a(y-b) = 0 .
\, z = 1 \, ,
\, \begin{pmatrix} a \\ 0 \\ 1 \end{pmatrix} \, , \, \begin{pmatrix} 0 \\ b \\ 1 \end{pmatrix} \,
\, \lgroup \begin{pmatrix} a \\ 0 \\ 1 \end{pmatrix} \times \begin{pmatrix} 0 \\ b \\ 1 \end{pmatrix} \rgroup \cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix} \, = \, 0 \,
\, bx + ay - abz = 0 .
\, z = 0 .
///////
Den interaktiva simulering som skapade denna film.
///////
///////