This is a sub-page of our page on Geometry.
///////
The sub-pages of this page are:
• Euclidean Geometry
• Non-Euclidean Geometry
///////
Related sources of information:
• Projective metrics
• Metric Projective Geometry
• Cayley-Klein Metric
///////
The interactive simulations on this page can be navigated with the Free Viewer
of the Graphing Calculator.
///////
Below we make the following summation convention (due to Einstein):
\, {\omega}^i x_i \stackrel {\mathrm{def}}{=}{\sum\limits_{1 \le k \le n+1}^{ \text {} } {\omega}^k x_k} \, .
///////
Let \, X \, and \, \omega \, denote a point and a hyperplane in \, P^3 \, , and let
\,{\lbrack \, X \, \rbrack}_{C.T.U} = ( x_1 : x_2 : x_3 : x_4 ) = (x : y : z : t) \, , and
\,{\lbrack \, \omega \, \rbrack}_{c.t.u} = ( {\omega}^1 : {\omega}^2 : {\omega}^3 : {\omega}^4 ) = (u : v : w : p) \,
denote their respective coordinates in two dually unified systems.
Then the point \, X \, and the plane \, \omega \, are incident if and only if
\, {\omega}^i x_i = 0 \, .
///////
The Poncelét-Gergonne (bilinear form) duality can be expressed as
\, ux+vy+wz+pt=0 \,
or, using index notation:
\, {\omega}^1 x_1+{\omega}^2 x_2+{\omega}^3 x_3 + {\omega}^4 x_4 = 0 \, .
Centrally symmetric quadratic forms in point coordinates:
\, \frac{x^2}{a}+\frac{y^2}{b}+\frac{z^2}{c} = t^2 \,
The same quadratic form in plane coordinates:
\, au^2+bv^2+cw^2 = p^2 \,
///////
\, \begin{matrix} {\begin{matrix} \\ \text{Point coordinates:} \\ \\ {x^2/a+y^2/b+z^2/c = t^2} \\ \\ {x^2+y^2+z^2-\frac{1}{\epsilon}t^2 = 0} \\ \\ \begin{matrix} {\epsilon \rightarrow 0 \text{ leads to a logical collapse:}} \\ \\ {x^2+y^2+z^2 = 0} \\ {t^2 = 0} \end{matrix} \end{matrix}} & {\; \; \; \; \; \; \; \; \; \;} & {\begin{matrix} \text{Plane coordinates:} \\ \\ {au^2+bv^2+cw^2 = p^2} \\ \\ {u^2+v^2+w^2-{\epsilon}p^2 = 0} \\ \\ {\epsilon \rightarrow 0 \text{ leads to a value collapse:}} \\ \\ {u^2+v^2+w^2 = 0} \end{matrix}} \end{matrix} \,///////
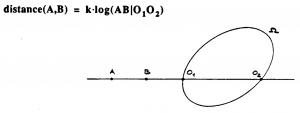
Distance metric: \, d_{istance}(A,B) \stackrel {\mathrm{def}}{=} k \log(AB|O_1 O_2) .
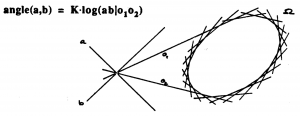
Angle metric: \, a_{ngle}(a,b) \stackrel {\mathrm{def}}{=} k \log(ab|o_1 o_2) .
///////
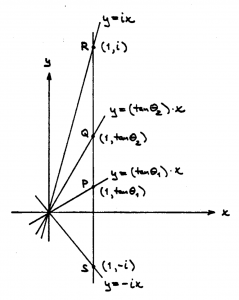
Laguerre’s angle formula:
Laguerre’s angle formula(diagram):
///////
///////
Laguerre’s angle formula – computation:
\, (PQ|IJ) = \dfrac{IP/IQ}{JP/JQ} = \dfrac{\dfrac{i-tan{\theta}_1}{i-tan{\theta}_2}}{\dfrac{-i-tan{\theta}_1}{-i-tan{\theta}_2}} = \,
\, = \dfrac{(i cos{\theta}_1 - sin{\theta}_1)(-i cos{\theta}_2 - sin{\theta}_2)}{(-i cos{\theta}_1 - sin{\theta}_1)(i cos{\theta}_2 - sin{\theta}_2)} = \,
\, = \dfrac{(cos{\theta}_1 + i sin{\theta}_1)(cos{\theta}_2 - i sin{\theta}_2)}{( cos{\theta}_1 - i sin{\theta}_1)(cos{\theta}_2 + i sin{\theta}_2)} = \dfrac{e^{i{{\theta}_1}} e^{-i{{\theta}_2}}}{e^{-i{{\theta}_1}} e^{i{{\theta}_2}}} = \dfrac{e^{i({{\theta}_1 - {\theta}_2})}}{e^{-i({{\theta}_1 - {\theta}_2})}} = ,
\, = e^{2 i({{\theta}_1 - {\theta}_2})} .
We see that if we choose the constant \, k = \frac{1}{2i} \, this formula is indeed expressing the familiar euclidean angle. This calculation was discovered by the sixteen year old Edmund Laguerre in 1853, and it is referred to as Laguerre’s angle formula:
\, \frac{1}{2i} \log(PQ|IJ) = {{\theta}_1 - {\theta}_2} .