This is a sub-page of our page on Separating the variables

///////

Related KMR pages

• …

///////

Other relevant sources of information

• …

///////

/////// Problem 1:

Formulation: Calculate the volume of the ellipsoid \, \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} + \dfrac{z^2}{c^2} \leq 1 \,

Solution: \;\;\;\;\; If we make the substitution \, \begin{Bmatrix} \begin{smallmatrix} x(t, \theta, \phi) \, = \, a \, t \sin\theta \cos\phi \\ y(t, \theta, \phi) \, = \, b \, t \sin\theta \sin\phi \\ \; z(t, \theta, \phi) \, = \, c \, t \cos\theta \;\;\;\;\;\;\;\, \end{smallmatrix} \end{Bmatrix} \,

the differential transformation of \, (x, y, z) \, with respect to \, (t, \theta, \phi) \, is given by

\, \begin{pmatrix} \begin{smallmatrix} dx \\ dy \\ dz \end{smallmatrix} \end{pmatrix} = \frac {\partial(x, y, z)}{\partial(t, \theta, \phi)} \begin{pmatrix} \begin{smallmatrix} dt \\ d\theta \\ d\phi \end{smallmatrix} \end{pmatrix} ,

where the Jacobian matrix \, \frac {\partial(x, y, z)}{\partial(t, \theta, \phi)} = \begin{pmatrix} \begin{smallmatrix} a \sin\theta \cos\phi & a \, t \cos\theta \cos\phi & -a \, t \sin\theta \sin\phi \\ b \sin\theta \sin\phi & b \, t \cos\theta \cos\phi & \;\; b \, t \sin\theta \cos\phi \\ c \cos\phi & -c \, t \sin\phi & 0 \end{smallmatrix} \end{pmatrix} ,

and the Jacobian determinant \vert \frac {\partial(x, y, z)}{\partial(t, \theta, \phi)} \vert = \begin{smallmatrix} a b c \, t^2 \sin\theta \end{smallmatrix} .

Assembling these pieces we get

\, \iiint\limits_{\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} \leq 1} dx dy dz \, = \, \begin{Bmatrix} \begin{smallmatrix} \text{substitution:} \\ x \, = \, a \, t \sin\theta \cos\phi \\ y \, = \, b \, t \sin\theta \sin\phi \\ \; z \, = \, c \, t \cos\theta \;\;\;\;\;\;\;\, \\ dx dy dz \, = \, a b c \, t^2 \sin\theta \, dt d\theta d\phi \end{smallmatrix} \end{Bmatrix} \, = \, = \iiint\limits_{ \begin{smallmatrix} 0≤t≤1, \\ 0≤\theta≤\pi, \\ 0≤\phi≤ 2 \pi \end{smallmatrix} } a b c \, t^2 \sin\theta \, dt d\theta d\phi \, = \, \, = \, a b c \int\limits_{0}^{1} t^2 dt \, \int\limits_{0}^{\pi} \sin\theta d\theta \, \int\limits_{0}^{2 \pi} d \phi \, = \, a b c \, [\frac{1}{3} t^3]_0^1 \, [- \cos\theta]_0^{\pi} \, [ \phi ]_0^{2 \pi} \, =

\, = a b c \cdot \frac{1}{3} \cdot 2 \cdot 2 \pi \, = \, \frac{ 4 \pi}{3} a b c .

REFLECTION: The substitution of variables transforms the ellipsoid in \, (x, y, z) -space into a rectangular box in \, (t, \theta, \phi) -space. In the latter space the effects of the variables on the integral are independent of each other, which enables the integral to be separated into a product of three independent one-dimensional integrals.

Note also that if \, a = b = c = r \, then the volume of the ellipsoid becomes \, \frac {4\pi}{3} r^3 \, ,
which is equal to the volume of a sphere with radius \, r \, (as it should be).

///
\, \begin{pmatrix} \begin{smallmatrix} dx \\ dy \\ dz \end{smallmatrix} \end{pmatrix} = \begin{pmatrix} \begin{smallmatrix} a \sin\theta \cos\phi & a \, t \cos\theta \cos\phi & -a \, t \sin\theta \sin\phi \\ b \sin\theta \sin\phi & b \, t \cos\theta \cos\phi & b \, t \sin\theta \cos\phi \\ c \cos\phi & -c \, t \sin\phi & 0 \end{smallmatrix} \end{pmatrix} \begin{pmatrix} \begin{smallmatrix} dt \\ d\theta \\ d\phi \end{smallmatrix} \end{pmatrix} .
///

/////// Problem 2:

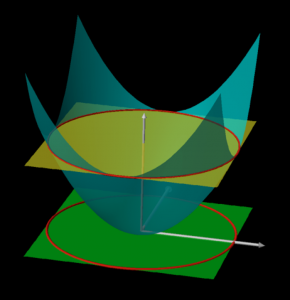
Formulation: Calculate the integral \, \iiint z \sqrt{x^2+y^2} dx dy dz \,
over the body enclosed by the blue paraboloid \, z = x^2+y^2 \,
and the yellow plane \, z = 1 .

Solution:

\, \iiint\limits_{x^2+y^2≤z≤1} z \sqrt{x^2+y^2} dx dy dz = \, = \iint\limits_{x^2+y^2≤1} \sqrt{x^2+y^2} dx dy \, \int\limits_{x^2+y^2}^{1} z dz = \, = \iint\limits_{x^2+y^2≤1} \sqrt{x^2+y^2} dx dy \, { [ \,\frac{1}{2} z^2 \, ] }_{x^2+y^2}^{1} = \, = \iint\limits_{x^2+y^2≤1} \sqrt{x^2+y^2} \, \frac{1}{2} (1 - (x^2+y^2)^2) dx dy = \begin{Bmatrix} \begin{smallmatrix} \text{polar coordinates:} \\ x(r, \theta) \, = \, r \cos\theta \\ y(r, \theta) \, = \, r \sin\theta \\ \vert \frac {\partial(x, y)} {\partial(r, \theta)} \vert \, = \, r \\ dx dy = r dr d\theta \end{smallmatrix} \end{Bmatrix} = \, = \frac{1}{2} \int\limits_{0}^{2\pi} d\theta \, \int\limits_{0}^{1} (1 - r^4) r \cdot r dr = \frac{1}{2} \, 2\pi \, \int\limits_{0}^{1} (r^2 - r^6) dr = \,

\, = \pi \, \left[ \, \dfrac{1}{3} r^3 - \dfrac{1}{7} r^7 \, \right]_{0}^{1} = \pi \left( \dfrac{1}{3} - \dfrac{1}{7} \right) = \dfrac{4\pi}{21} .

REFLECTION: In this integral the variable \, z \, is in fact operating independently from the variables \, x \, and \, y . It is only the lower limit of the \, z -integral that depends on \, x \, and \, y . This is why we can get away with integrating first in the \, z -direction and then substitute into polar coordinates in order to separate the \, x \, and \, y parts of the integral.

///////