This page is a sub-page of our page on Social Algebra.

///////

Related pages:

• Norm-Critical Innovation Algebra

/////
• Artifical Ethics
• Ethical E-Commerce
/////
• Knowledge Algebra
• Business Algebra
/////
• Social Calculus
/////
• Category Theory
• The Human Category
• Algebraic Thought
/////
• Systems Modeling
/////
• Political Modeling
/////
• Provocative Modeling
/////
• Learning Modeling
/////
• Matrix Algebra
/////
• Disambiguating plus
• Rings of Polynomials

///////

Other relevant sources of information:

• Platform Capitalism by Nick Srnicek
• The End Of Capitalism Has Begun, Paul Mason, The Guardian, 15 July 2015.

///////

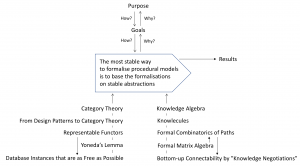
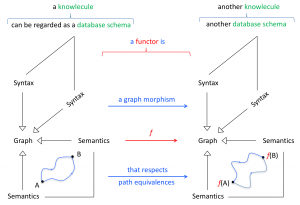
The advantage of stable abstractions

///////

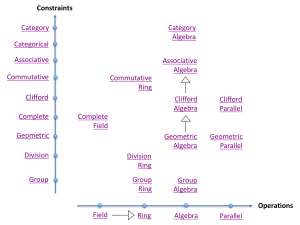
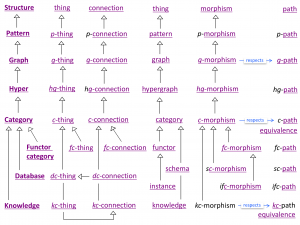
Computational layers of abstraction

///////

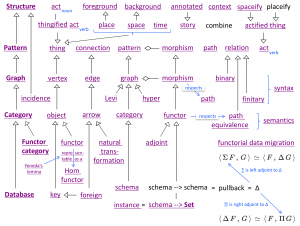
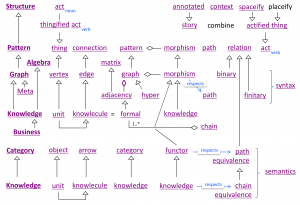
A math-knowledge knowlecule:

Each non-empty box in the matrix below corresponds to a mathematical concept
that is named by concatenating the two (bold) terms in the respective row and column:

		field	ring	algebra	module
knowledge				knowledge algebra
business				business algebra
category				category algebra
social				social algebra
associative				associative algebra
clifford				clifford algebra
geometric				geometric algebra
division			division ring	division algebra
group			group ring	group algebra
commutative			commutative ring	commutative algebra
complete		complete field
free		vector space	free R-module on S		free module
categorical
		field	ring	algebra	module

///////

The same table with the fourth column equal to ‘calculus’ instead of ‘module’:

		field	ring	algebra	calculus
knowledge				knowledge algebra
business				business algebra
category				category algebra
social				social algebra	social calculus
associative				associative algebra
clifford				clifford algebra	clifford calculus
geometric				geometric algebra	geometric calculus
division			division ring	division algebra
group			group ring	group algebra
commutative			commutative ring	commutative algebra
complete		complete field			complete calculus
categorical
		field	ring	algebra	calculus

///////

///////

Structure	thing	link	thing	morph	path	path equivalence
Pattern	p- thing	p- link	pattern	p- morph	p- path	p-path equivalence
Graph	g- thing	g- link	graph	g- morph	g- path	g-path equivalence
PowerGraph	pg-thing	pg-link	power graph	pg- morph	pg- path	pg-path equivalence
HyperGraph	hg-thing	hg-link	hypergraph	hg-morph	hg- path	hg-path equivalence
Category	c- thing	c- link	category	c- morph	c- path	c-path equivalence
Functor Category	fc- thing	fc- link	functor	fc- morph	fc- path	fc-path equivalence
Database Category	dc- thing	dc- link	database-schema/instance	dc- morph	dc- path	dc-path equivalence
Knowledge Category	kc- thing	kc- link	knowlecule	kc- morph	kc-path	kc-path equivalence

///////

• A powerpoint on computational levels of abstraction (version 3.1)

REMARK: Saving the above powerpoint and opening it on your local computer will give you access to the hyperlinks (to explanations) that it contains.

///////

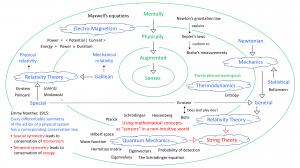
Physically and mentally augmented senses

///////

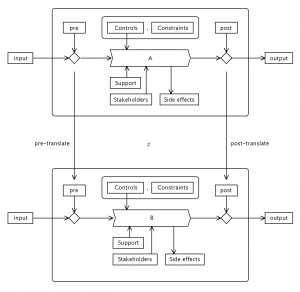
Naturally related processes:

Process B is naturally related to process A: