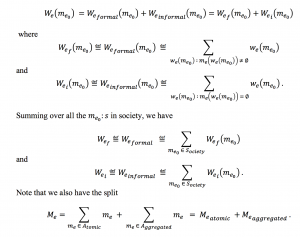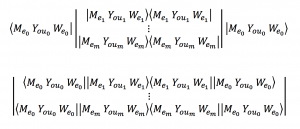Social Algebra | Knowledge Management Research Group

This page is a sub-page of our page on Algebra.

///////

The sub-pages of this page are:

• Socially Responsible Algebra

///////

///////

///////

///////

The notation used below is explained in our section on Business Algebra.

From me to you 1:

From me to you 2:

///////

$\, M_e \, \stackrel {\mathrm{def}}{=} \, {\sum\limits_{m_e \, \in \, S_{ociety} }} m_e \,$

$\, M_e \, \equiv \, {(M_e)}_{Atomic} \oplus {(M_e)}_{Agregated} \;\; \equiv \, {\sum\limits_{m_e \, \in \, {(M_e)}_{Atomic}}^{ \text {} }} m_e \;\; \oplus \, {\sum\limits_{m_e \, \in \, {(M_e)}_{Aggregated}}^{ \text {} }} m_e$

$\, {(W_e)}_{Formal} \, \stackrel {\mathrm{def}}{=} \, {\sum\limits_{w_e( \, m^1_e \, ) \, : \, m_e( \, w_e(\, m^1_e \, ) \, ) \, \neq \; \emptyset }} \,\, w_e(\, m^1_e \, ) \,$

$\, {(W_e)}_{Informal} \, \stackrel {\mathrm{def}}{=} \, {\sum\limits_{w_e( \, m^1_e \, ) \, : \, m_e( \, w_e(\, m^1_e \, ) \, ) \, = \; \emptyset }} \,\, w_e(\, m^1_e \, ) \,$

$\, W_e \, \stackrel {\mathrm{def}}{=} \, {(W_e)}_{Formal} \oplus {(W_e)}_{Informal} \,$

///////

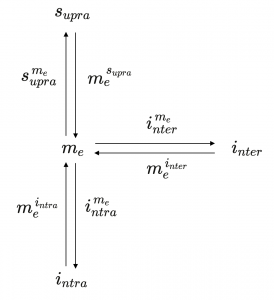
$\, i_{ntra}^{ \, m^1_e } \,$

$\, i_{nter}^{ \, m^1_e } \,$

$\, s_{upra}^{ \, m^1_e } \,$

$\, 1 \,$

///////

///////

$\, F_{ormal}N_{ational}P_{roduct} \, \stackrel {\mathrm{def}}{=} \, {\sum\limits_{m_e \, \in \, M_e \, \in \, N_{ation}}^{ \text {} }}{c_{ontributions}}( m_e ) \,$

$\, F_{ormal}I_{nternational}P_{roduct} \, \stackrel {\mathrm{def}}{=} \, {\sum\limits_{m_e \, \in \, M_e \, \in \, W_{orld}}^{ \text {} }}{c_{ontributions}}( m_e ) \,$

$\, I_{nformal}N_{ational}P_{roduct} \, \stackrel {\mathrm{def}}{=} \, {\sum\limits_{m_e \, \in \, {(W_e)}_{Informal} \, \in \, N_{ation}}^{ \text {} }}{c_{ontributions}}( m_e ) \,$

$\, I_{nformal}I_{nternational}P_{roduct} \, \stackrel {\mathrm{def}}{=} \, {\sum\limits_{m_e \, \in \, {(W_e)}_{Informal} \, \in \, W_{orld}}^{ \text {} }}{c_{ontributions}}( m_e ) \,$

///////

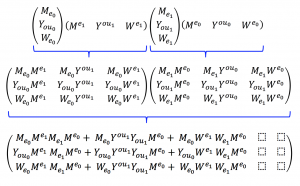
$\, A_{gents} \, = \, ( \, P_{hysical} \oplus L_{egal} \oplus I_{nformal} \, ) \, B_{odies} \, = \,$

$\, = \, P_{hysical}B_{odies} \oplus L_{egal}B_{odies} \oplus I_{nformal}B_{odies} \, = \,$

$\, = \, H_{umans} \oplus M_{achines} \oplus O_{rganizations} \oplus N_{etworks} \,$

///////

$\, i_{ntra}^{ \, m_e } \,$

$\, i_{nter}^{ \, m_e } \,$

$\, s_{upra}^{ \, m_e } \,$

///////

$\, m_e^{ \, i_{ntra} } \,$

$\, m_e^{ \, i_{nter} } \,$

$\, m_e^{ \, s_{upra} } \,$

///////

$\, r_{eact} \, = \, i_{nterpret} \, = \, m_e^{ \, i_n } \, = \, \lim\limits_{m_e} \, i_n \,$

$\, a_{ct} \, = \, r_{espond} \, = \, o_{ut}^{ \, m_e } \, = \, \mathrm {co} \lim\limits_{m_e} \, o_{ut} \,$

///////

$\, i_{ntra} \,$

$\, i_{nter} \,$

$\, s_{upra} \,$

///////

///////

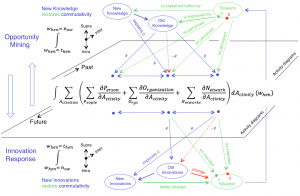
A conversational feedback loop in Knowledge Loop Algebra
between the communities $\, {C_{om}}_1 \,$ and $\, {C_{om}}_2 \,$ using the $\, O_{utside} \,$ protocol :

$\, \langle \, {O_{utside}}_{input} \, \vert \vert \, {C_{om}}_1 \, \rangle \langle \, {C_{om}}_1 \, \vert \vert \, {O_{utside}}_{output} \, \rangle \langle \, {O_{utside}}_{input} \, \vert \vert \, {C_{om}}_2 \, \rangle \langle \, {C_{om}}_2 \, \vert \vert \, {O_{utside}}_{output} \, \rangle \,$

///////

The $\, N_{ew} \,$ interface emulated by an $\, O_{ld} \,$ implementation

$\, \langle \, N_{ew_{input}} \, \vert \vert \, N_{ew_{output}} \, \rangle \, = \, \overbrace{\langle \, N_{ew_{input}} \, \vert \vert \, O_{ld_{input}} \, \rangle}^{\text{transform}} \overbrace{\langle \, O_{ld_{input}} \, \vert \vert \, O_{ld_{output}} \, \rangle}^{\text{solve}} \overbrace{\langle \, O_{ld_{output}} \, \vert \vert \, N_{ew_{output}} \, \rangle}^{\text{invert}} \, =$

$\, = \, \overbrace{\langle \, N_{ew_{input}} \, \vert \vert \, O_{ld_{input}} \, \rangle}^{\text{translate input}} \overbrace{\langle \, O_{ld_{input}} \, \vert \vert \, O_{ld_1} \, \rangle \langle \, O_{ld_1} \, \vert \vert \, O_{ld_2} \, \rangle \langle \, O_{ld_2} \, \vert \, \cdots \, \vert \, O_{ld_n} \, \rangle}^{\text{the n milestones of the old solution process}} \overbrace{\langle \, O_{ld_{output}} \, \vert \vert \, N_{ew_{output}} \, \rangle}^{\text{translate output}}$

NOTE: This formula assumes that $\, O_{ld_n} \, \equiv \, O_{ld_{output}}$ .

• Foresight and hindsight process manager
• The EE(S+O+C)(M+O+P) Model
• The Ericsson AXE10 Delay

///////

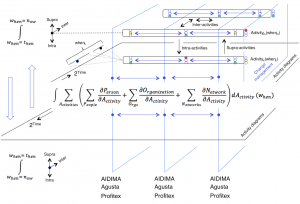
The TELL ME Innovation Cycle 1:

The TELL ME Innovation Cycle 2:

///////

Leave a Reply Cancel reply