This page (in Swedish) is a sub-page of our page on Geometric Algebra.
///////
Relaterade KMR-sidor:
• Clifford Algebra
• Geometric Algebra
• Quaternions
///////
Andra relevanta informationskällor:
• Quaternion (at Wikipedia)
• Rotor (at Wikipedia)
• Versor (at Wikipedia)
• Hyperbolic versor (at Wikipedia)
• Rotation formalisms in three dimensions (at Wikipedia)
///////
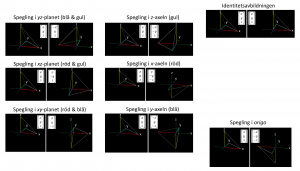
Speglingar i koordinatplan, i koordinataxlar och i origo
////////////////////////////////////////////////////////
Geometriska tal i den Euklidiska 3D-rymden:
\, S_{{pegla}\,i\,P_{lan}} (F_{ramåt}) \, \, S_{{pegla}\,i\,P_{lan}} (V_{änsteråt}) \, \, S_{{pegla}\,i\,P_{lan}} (U_{ppåt}) \,och de motsatt riktade och ekvivalenta speglingsbeskrivningarna:
\, S_{{pegla}\,i\,P_{lan}} (B_{akåt}) \, = \, S_{{pegla}\,i\,P_{lan}} (F_{ramåt}) \, \, S_{{pegla}\,i\,P_{lan}} (H_{ögeråt}) \, = \, S_{{pegla}\,i\,P_{lan}} (V_{änsteråt}) \, \, S_{{pegla}\,i\,P_{lan}} (N_{edåt}) \, = \, S_{{pegla}\,i\,P_{lan}} (U_{ppåt}) \,///////
The interactive simulations on this page can be navigated with the Free Viewer
of the Graphing Calculator.
///////
Dualisering:
\, (F_{ramåt} V_{änsteråt})^{\star} \, = \, (F_{ramåt} V_{änsteråt}) \, {(- \, F_{ramåt} V_{änsteråt} U_{ppåt})}^{-1} \, = \,
\, = \, - \, F_{ramåt} V_{änsteråt} (U_{ppåt})^{-1} (V_{änsteråt})^{-1} (F_{ramåt})^{-1} \, =
\, = \, - \, F_{ramåt} V_{änsteråt} N_{edåt} H_{ögeråt} B_{akåt} \, = \, F_{ramåt} V_{änsteråt} H_{ögeråt} N_{edåt} B_{akåt} \, =
\, = \, F_{ramåt} N_{edåt} B_{akåt} \, = \, - \, F_{ramåt} B_{akåt} N_{edåt} \, = \, - \, N_{edåt} \, = \, U_{ppåt}
\, (V_{änsteråt} U_{ppåt})^{\star} \, = \, (V_{änsteråt} U_{ppåt}) \, {(- F_{ramåt} V_{änsteråt} U_{ppåt})}^{-1} \, = \,
\, = \, - V_{änsteråt} U_{ppåt} (U_{ppåt})^{-1} (V_{änsteråt})^{-1} (F_{ramåt})^{-1} \, = \, - (F_{ramåt})^{-1} \, = \, - B_{akåt} \, = \, F_{ramåt}
\, (F_{ramåt} U_{ppåt})^{\star} \, = \, (F_{ramåt} U_{ppåt}) \, {(- \, F_{ramåt} V_{änsteråt} U_{ppåt})}^{-1} \, = \,
\, = \, - \, F_{ramåt} U_{ppåt} (U_{ppåt})^{-1} (V_{änsteråt})^{-1} (F_{ramåt})^{-1} \, =
\, = \, - \, F_{ramåt} H_{ögeråt} B_{akåt} \, = \, F_{ramåt} B_{akåt} H_{ögeråt} \, = \, H_{ögeråt} \, = \, - V_{änsteråt}
///////
Speglingar i plan, linjer och punkter
Tre vinkelräta planspeglingar ger en spegling i planens skärningspunkt (= origo):
\, S_{{pegla}\,i\,P_{lan}} (F_{ramåt}) S_{{pegla}\,i\,P_{lan}} (V_{änsteråt}) S_{{pegla}\,i\,P_{lan}} (U_{ppåt}) \, = S_{{pegla}\,i\,P_{unkt}} (O_{rigo}) \, = -1 \,En spegling i en linje är lika med en halvtvarvsrotation kring denna linje:
\, S_{{pegla}\,i\,L_{inje}} (e_{nLinje}) \, = \, R_{otera(H{alvt}V_{arv})\,k_{ring}} (d_{ennaLinje}) \,Två vinkelräta planspeglingar ger en halvtvarvsrotation kring planens skärningslinje:
\, S_{{pegla}\,i\,P_{lan}} (F_{ramåt}) S_{{pegla}\,i\,P_{lan}} (V_{änsteråt}) \, = \, S_{{pegla}\,i\,L_{inje}} (L_{inje}(F_{ramåt} V_{änsteråt})^{\star}) \, = \, R_{otera(H{alvt}V_{arv})\,k_{ring}} (L_{inje} (U_{ppåt})) \, \, S_{{pegla}\,i\,P_{lan}} (V_{änsteråt}) S_{{pegla}\,i\,P_{lan}} (U_{ppåt}) \, = \, S_{{pegla}\,i\,L_{inje}} (L_{inje}(V_{änsteråt} U_{ppåt})^{\star}) \, = \, R_{otera(H{alvt}V_{arv})\,k_{ring}} (L_{inje} (F_{ramåt})) \, \, S_{{pegla}\,i\,P_{lan}} (F_{ramåt}) S_{{pegla}\,i\,P_{lan}} (U_{ppåt}) \, = \, S_{{pegla}\,i\,L_{inje}} (L_{inje}(F_{ramåt} U_{ppåt})^{\star}) \, = \, R_{otera(H{alvt}V_{arv})\,k_{ring}} (L_{inje} (H_{ögeråt})) \,Dessutom har vi sambanden:
\, S_{{pegla}\,i\,P_{lan}} (F_{ramåt}) S_{{pegla}\,i\,P_{lan}} (F_{ramåt}) \, = \, 1 \, \, S_{{pegla}\,i\,P_{lan}} (V_{änsteråt}) S_{{pegla}\,i\,P_{lan}} (V_{änsteråt}) \, = \, 1 \, \, S_{{pegla}\,i\,P_{lan}} (U_{ppåt}) S_{{pegla}\,i\,P_{lan}} (U_{ppåt}) \, = \, 1 \,///////
Speglingar i plan:
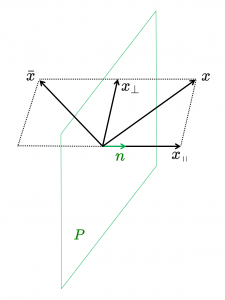
Sats: Låt \, P \, vara ett plan i \, {\mathbb{R}}^3 \, med enhetsnormalen \, n .
En spegling \, S_{P} \, i planet \, P \, kan i geometrisk algebra representeras så här:
\, {\mathbb{R}}^3 \ni x \mapsto - \, n \, x \, n \, = \, \bar{x} = S_{P}(x) \in {\mathbb{R}}^3 .
Spegling av vektorn \, x \, i planet \, P \, med enhetsnormal \, n \, kan uttryckas som:
\, \bar{x} \, = \, - \, n \, x \, n \, = \, - \, n \, (x_{\, \shortparallel} + x_{\perp}) \, n \, = \, - \, n \, x_{\, \shortparallel} \, n - \, n \, x_{\perp} \, n \, = - \, n \, n \, x_{\, \shortparallel} + n \, n \, x_{\perp} \, = \, - \, x_{\, \shortparallel} + x_{\perp} \, = \, S_{P} (x) \,vilket avslutar beviset.
Rotationer
Två planspeglingar ger en rotation kring planens skärningslinje.
Allmänna rotationer kan uttryckas genom att använda versorer.
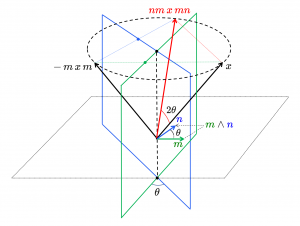
Låt det första respektive andra speglingsplanet ha enhetsnormalerna \, m \, respektive \, n .
Om vi tillämpar planspeglingslagen två gånger får vi:
Den algebraiska och geometriska strukturen hos en versor:
/////// Quoting Wikibooks Associative Composition Algebra / Division quaternions:
Lemma 1: Om \, a \, och \, b \, är kvadratrötter ur minus ett och om \, a \perp b så är \, a \, b \, a \, = \, b \, .
Bevis: \,\; 0 \, = \, a \, (a \, b + b \, a) \, = \, a^2 \, b + a \, b \, a \, = \, -b + a \, b \, a \, .
Lemma 2: Under samma hypotes är \, a \perp a \, b \, och \, b \perp a \, b \, .
Bevis (av att \, a \perp a\, b) \, : \, a \, (a \, b) + (a \, b) \, a \, = \, -b + a \, b \, a \, = \, 0 \, .
Låt \, u = e^{\, \theta \, \mathbf{r}} \, vara en versor. Det finns en gruppverkan (group action) på \, \mathbb{H} \, som bestäms av \, u \, :
Inner automorphism \, f \, : \, \mathbb{H} \, \ni \, q \, \mapsto \, u^{-1} q \, u \, \in \, \mathbb{H} \, .
Notera att \, u \, kommuterar med alla vektorer i planet \, \{\, x + y \, \mathbf{r} \, : \, x, y \, \in \, \mathbb{R} \, \} .
Välj nu \, \mathbf{s} \, från storcirkeln på \, \mathbb{S}^2 \, som är vinkelrät mot \, \mathbf{r} . Då är \, \mathbf{r} \, \mathbf{s} \, \mathbf{r} \, = \, \mathbf{s} \, enligt lemma 1. Beräkna nu \, f(\mathbf{s}) \, :
\;\;\;\;\;\;\;\;\;\;\;\; = \, ({\cos}^2 \theta - {\sin}^2 \theta) \, \mathbf{s} + (2\sin \theta \cos \theta) \, \mathbf{s} \, \mathbf{r} \, = \, \mathbf{s} \, \cos 2 \theta + \mathbf{s} \, \mathbf{r} \, \sin 2 \theta ,
vilket är en rotation med vinkeln \, 2 \theta \, i \, (\mathbf{s}, \mathbf{s} \, \mathbf{r}) \, planet.
Denna egenskap hos \, \mathbb{H} , att det finns en inre automorfi \, f \, som producerar rotationer, har visat sig vara mycket användbar.
/////// End of quote from Wikibooks
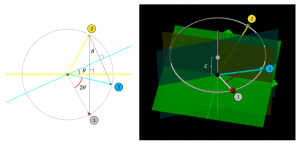
Två \, \theta -separerade speglingar ger en \, 2 \theta -separerad rotation:
I planet rör det sig om speglingar i linjer (vänstra fönstret)
och i 3D-rymden rör det sig om speglingar i plan (högra fönstret).
///////
Verkan av en fix versor på en roterande vektor:
Filmen visar den rödmärkta vektorn, vars spets roterar kring den grå cirkeln. Varje position av denna vektor speglas först i den horisontella gula linjen (i det vänstra fönstret) med motsvarande spegling i det vertikala gula planet (i det högra fönstret), vilket resulterar i den gula vektorn.
Denna vektor speglas sedan i den ljusblå linjen (i det vänstra fönstret) med motsvarande spegling i det vertikala ljusblåa planet (i det högra fönstret), vilket resulterar i den ljusblåa vektorn.
Eftersom den ljusblåa vektorn är relaterad med den “rödnästa” vektorn genom en konstant rotation så följer den ljusblåa vektorn den rödnästa – på konstant avstånd och med konstant vinkel – runt den cirkulära kon vars symmetriaxel är identisk med \, z -axeln.
///////
Verkan av en variabel versor på en fix vektor:
Variationen av versorn orsakas av en förändring av vinkeln mellan den gula linjen och den ljusblå linen (i det vänstra fönstret) och därmed även av motsvarande vinkel mellan det gula vertikala planet och det ljusblå vertikala planet (i det högra fönstret).
///////