This page is a sub-page of our page on Some basic algebraic concepts.

///////

Related pages:

• Disambiguating plus
• Rings of Polynomials

///////

A binary composition \ast on a set \mathcal S is a function

{\mathcal S \times \mathcal S \ni (x, y) \, \mapsto \, x \ast y \in \mathcal S.}

The composition \ast is called associative if

(x \ast y) \ast z = x \ast (y \ast z) \, , \forall x, y, z \in \mathcal S

and \ast is called commutative if

x \ast y = y \ast x \, , \forall x, y \in \mathcal S.

If there exists an element e \in \mathcal S such that

e \ast x = x \ast e = x \, , \forall x \in \mathcal S

then e is called a unit (or unit element).

If e and e' are unit elements, then we have

e \ast e' = e = e'

Hence there is at most one unit element, i.e., a unit element is unique (if it exists).

///////

Assume that (\mathcal S, \ast) has a unit element e. Then the element x \in \mathcal S is said to have:

a left inverse, if there is an element y \in \mathcal S such that y \ast x = e.

a right inverse, if there is an element y \in \mathcal S such that x \ast y = e.

an inverse , if there is an element y \in \mathcal S such that x \ast y = y \ast x = e.

///////

Let \ast and \bullet be two binary compositions on \mathcal S. We say that:

\ast is left-distributive over \bullet if

(x \ast ( y \bullet z) = (x \ast y) \bullet (x \ast z) \, , \forall x, y, z \in \mathcal S.

\ast is right-distributive over \bullet if

(y \bullet z) \ast x = (y \ast x) \bullet (z \ast x) \, , \forall x, y, z \in \mathcal S.

\ast is distributive over \bullet if \ast is both left- and right-distributive over \bullet.

///////

Using the concepts defined above,
we can define a number of important algebraic structures:

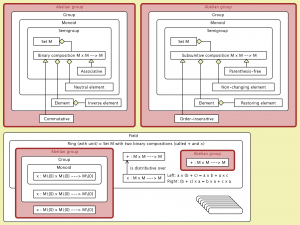
• Semigroup: A set \mathcal S with a binary composition \ast that is associative.

• Monoid: A semigroup which has a unit element.

• Group: A monoid where each element has an inverse.

• Abelian group: A group whose binary composition is commutative.

• Ring: A set \mathcal R with two binary compositions,
called addition (denoted by + )
and multiplication (denoted by \cdot or by juxtaposition)
such that (\mathcal R, +) is an abelian group,
(\mathcal R, \cdot) is a semigroup,
and multiplication is distributive over addition.

• Ring with unit: A ring \mathcal R where (\mathcal R, \cdot) is a monoid.

• Commutative ring:  A ring with commutative multiplication.

• Field: A commutative ring with unit
where each non-zero element has a multiplicative inverse.

///////

Semantics of the concepts Group, Ring, and Field:

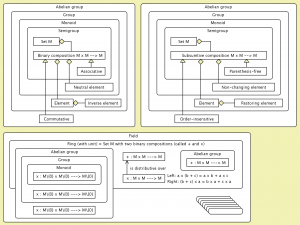
Semantics of the concepts Group, Ring, and Field (Semigroup):

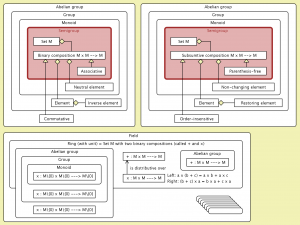
Semantics of the concepts Group, Ring, and Field (Monoid):

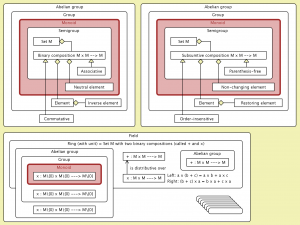
Semantics of the concepts Group, Ring, and Field (Group):

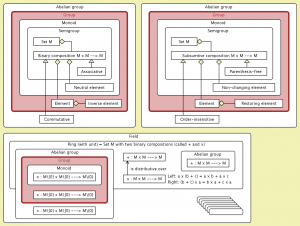
Semantics of the concepts Group, Ring, and Field (Abelian group):

///////

Module: An abelian group (\mathcal M, \oplus) is called a module over the ring (\mathcal R, +, \cdot), or an \mathcal R – module, if there is a function

{\mathcal R \times \mathcal M \ni (r, m) \, \mapsto \, r m \in \mathcal M}, \text{ such that}

(i):   0m = 0 where 0 is the additive unit of  \mathcal R.

(ii):  1m = m if \mathcal R has a multiplicative unit 1.

(iii): (r + r') m = (r m) \oplus (r' m).

(iv): r ( m \oplus m') = (r m) \oplus (r m').

(v): (r \cdot r') m = r (r' m).

Note: Most often the additive unit of \mathcal R and the additive unit of \mathcal M are both denoted by 0. Moreover, the direct sum \oplus is denoted by + and is referred to as addition.

Vector space: A module over a field.

Group homomorphism: A function {\varphi : \mathcal G \, \rightarrow \, \mathcal G'} where (\mathcal G, \ast) and (\mathcal G', {\ast}') are groups, and

\varphi ( x \ast y) = \varphi (x) {\ast}' \varphi (y), \, \forall x, y \in \mathcal G.

Module homomorphism: A function {\varphi : \mathcal M \, \rightarrow \, \mathcal M'} where \mathcal M and \mathcal M' are \mathcal R -modules and

\varphi ( rm_1 + m_2) = r \varphi (m_1) + \varphi (m_2), \, \forall r\in \mathcal R, \, \forall m_1, m_2 \in \mathcal M.

Note: The + sign to the left represents the addition in \mathcal M, while the + sign to the right represents the addition in \mathcal M'. Strictly speaking, the latter addition should be written as +'. This is a typical example of the kind of relaxation of notation that is often used in mathematics. The different meanings of a given symbol is most often clear from the context. If not, the more precise (but more cumbersome) notation can always be brought in to clear up the confusion.