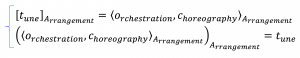This page is a sub-page of our page on Expandable Learning Objects.
///////
The sub-pages of this page are:
• Pythagorean Intervals
• The Logarithmic Piano
• Solfege: An Abstract Key System
• Chord Ladder
• Chord-Set Inclusion Graph
• Harmony and Melody
• Instantiations of Solfege in Different Keys
• Abstract and Concrete Chord Circles
• Transposition = Shift of Base in Music
• Interactions of Quarts and Quints
• Generating the Quint Circle from the Mathematical Cogwheels
• Uniformisation of Intervals
• Rhythm
• Bengt Ulin om Musik (in Swedish)
///////
Related sources of information:
• Music and mathematics at Wikipedia.
• Musical notation at Wikipedia.
• Musical note at Wikipedia.
• Music Theory (at the Sibelius Academy).
• Modes and Scales in Western Music at Wikipedia.
• Musical Set Theory at Wikipedia.
• Accidental (music) at Wikipedia.
• Piece for triple piano in hyperbolic space by Vi Hart.
• This visualisation of a Bach prelude lets you see just how clever the piece really is.
• But what is a Fourier series? From heat flow to circle drawings.
In Swedish:
• Musikteori på Wikipedia.
• Harmoni på Wikipedia.
• Melodi på Wikipedia.
• Diatonik på Wikipedia.
• Pentatonisk skala på Wikipedia.
• Funktionsanalys (musik) på Wikipedia.
• Grundfunktionerna (musik) på Wikipedia.
• Polyfoni på Wikipedia.
• Kontrapunkt på Wikipedia.
• Tonfrekvenser på ett liksvävande stämt piano på Musikipedia.
///////
Representation and Reconstruction of a Presentant with respect to a Background
Representation: \, [ \, p_{resentant} \, ]_{B_{ackground}} \, \mapsto \, \left< \, r_{epresentant} \, \right>_{B_{ackground}}
Reconstruction: \, \left( \, \left< \, r_{epresentant} \, \right>_{B_{ackground}} \, \right)_{B_{ackground}} \mapsto \,\, p_{resentant}
/////// In Swedish:
Representation och Rekonstruktion av en Presentant med hjälp av en Bakgrund
Representation: \, [ \, p_{resentant} \, ]_{B_{akgrund}} \, \mapsto \, \left< \, r_{epresentant} \, \right>_{B_{akgrund}}
Rekonstruktion: \, \left( \, \left< \, r_{epresentant} \, \right>_{B_{akgrund}} \, \right)_{B_{akgrund}} \mapsto \,\, p_{resentant}
/////// Back to English:
Partial representations
Representation and Reconstruction of a \, t_{une} \, with respect to an \, A_{rrangement} \, :
Representation: [ \, t_{une} \, ]_{A_{rr}} \mapsto \left< \,s_{core} \, \right>_{A_{rr}} .
Reconstruction: \left(\left< \, s_{core} \, \right>_{A_{rr}}\right)_{A_{rr}} \mapsto t_{une} .
s_{core} \, is another name for Sheet music. Here we will model it as:
s_{core} = \{ \, o_{rchestration}, c_{horeography} \, \}where \, o_{rchestration} \, specifies which instruments that are involved in the \, A_{rrangement} \, , and \, c_{horeography} \, specifies how these instruments should interact with each other.
Partial Representation and Partial Reconstruction of a \, t_{une} \, with respect to a \, K_{ey} \, :
The Representation and Reconstruction formulas for Numbers carry over to corresponding partial representation and partial reconstruction formulas for Tunes.
In tonal music, the tonal \, B_{ase} \, , the so-called tonic, of a \, t_{une} \, is given by its \, K_{ey} \, .
In the case of numbers and their digits with respect to a base, knowledge of the digits and the base is enough to uniquely determine the underlying number.
In contrast, in the case of tunes and their chord-sequences with respect to a key, knowledge of the chord-sequence and the key is not enough to uniquely determine the underlying tune. There are a lots of other aspects of a tune (such as melody, rhythm, etc) that are part of its arrangement.
Hence, while a \, n_{umber} \, is totally represented by its \, d_{igits} \, with respect to a certain \, B_{ase} \, , a \, t_{une} \, is only partially represented by its \, c_{hordSequence} \, with respect to a certain \, K_{ey} \,.
Therefore, in the case of tunes and their chord-sequences with respect to different keys, we can only state that:
Partial Representation: [ \, t_{une} \, ]_{A_{rr}} \supset [ \, t_{une} \, ]_{K_{ey}} \mapsto \left< \,c_{hordSequence} \, \right>_{K_{ey}} \, .
Partial Reconstruction: {\left( \left< \, c_{hordSequence} \, \right>_{K_{ey}} \, \right)}_{K_{ey}} \supset t_{une} \, .
This raises the question of which tune that is “the most reasonable one” that is represented by a given chord-sequence. Of course, the answer is highly dependent on the contexts at hand as well as on the individual participants’ interpretations of these contexts.
This opens up a huge area of mathematics, which deals with the most reasonable solutions to systems of equations. Such a solution is called a pseudoinverse for the system.
///////
Don Knuth: Fantasia Apocalyptica.
///////
///////
///////
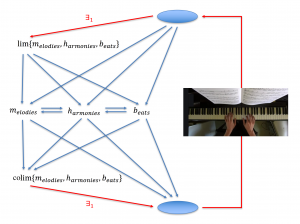
Lim and colim of melodies, harmonies, and beats:
///////
Steve Fishell explains how pedal steel guitar works
(on YouTube):
///////
The Entertainer (by Scott Joplin) in piano coordinates:
///////
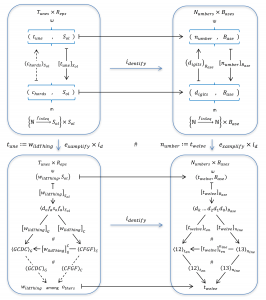
Numbers are naturally related to Music:
/////
Geometry of Music (Bill Wesley at TEDxAmericasFinestCity 2011):
///////
The TRUTH Why Modern Music Is Awful (Thoughty2 on YouTube, 2017):
///////
But what is a Fourier Series? – From heat flow to circle drawings
(Steven Strogatz on YouTube):
///////