This page is a sub-page of our page on Art.

///////

Related pages:

• Complex Numbers
• Conformal Mapping

///////

///////

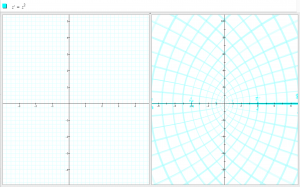
Squaring the grid creates confocal parabolas:

///////

Squaring-my-face(z^2):

Squaring (z’=z^2) my face (cropped):

///////

Inverting-my-face(2/z_conjugate):

Inverting-my-face(2/z_conjugate)(cropped):

///////

Sinusing-my-face(sinz)1:

Sinusing-my-face(sinz)1(cropped):

///////

Sinusing-my-face [z’ = sinz]2:

Sinusing-my-face [z’ = sinz] 2(cropped):

Sinusing the grid [z’=sin(1.25iz)]:

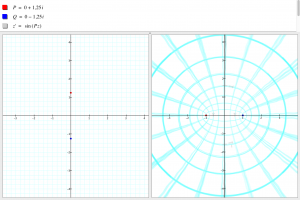
Sinusing my face with the grid [z’=sin(1.25iz)]:

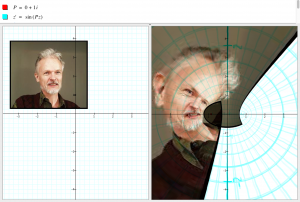
Sinusing my face with the grid [z’=sin(z+P+(nπ/2)(ReP)), P=1+i)]:

Sinusing the grid [z´= sin((0.5+i)z)]:

Sinusing my face with the grid [z’=sin((0.5+i)z)]:

Sinusing the grid [z’=sin(Pz), P= circle on (2, 0) with radius 1/2]:

Sinusing my face with the grid [z’=sin(Pz), P= circle on (2, 0) with radius 1/2]:

Sinusing my face with the grid [z’=sin(Pz), P= circle on (2, 0) radius 1/2] 2:

Sinusing my face [z’ = sin((1+i)z)] :

Sinusing my face with the grid [z’=sin(z(P+(nπ/2)(ReP)))), P=1+i]:

///////