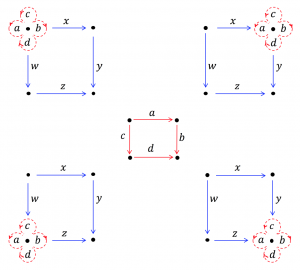
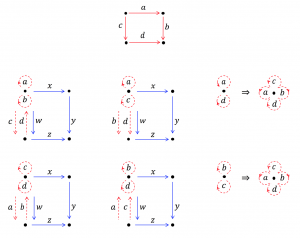
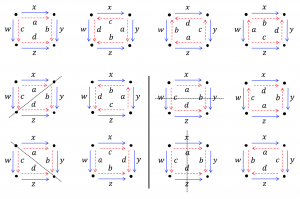
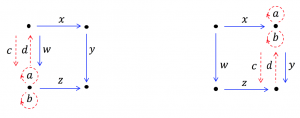This page is a sub-page of the page on our Learning Object Repository
///////
The sub-pages of this page are:
• A Categorial Manifesto
• Categorical Informatics
• Functors
• Limits and Colimits
• Functor Categories
• Category of Bundles (over a Base Space)
• Naturally Related Functors and Processes
• Adjoint Functors
• Institution Theory
• The Human Category
• Infinity Categories
///////
Related KMR-pages:
• Representation and Reconstruction of Numbers
• Numbers and their Digits in different Bases
• Shift of Base for Numbers.
• Mathematical Cogwheels
• BioEntropy
///////
Books:
• Basic Category Theory, by Tom Leinster, Cambridge University Press, 2014.
• Conceptual Mathematics – A first introduction to categories,
by F. William Lawvere and Stephen H. Schanuel, Cambridge University Press, 1997.
• Categories for the Working Mathematician, by Saunders Mac Lane, Springer Verlag, 1971.
• Category Theory for the Sciences, by David Spivak, 2014.
• Seven Sketches in Compositionality: An Invitation to Applied Category Theory,
by Brendan Fong and David Spivak, arXiv.org, 2018.
• Category Theory in Context by Emily Riehl
///////
Other related sources of information:
• Category theory at Wikipedia.
• Abelian category at Wikipedia.
• Comma category and slice category at Wikipedia.
• Groupoid in category theory at Wikipedia.
• Magma at Wikipedia.
• Alexander Grothendieck at Wikipedia.
• Lambda, the Ultimate
• From Design Patterns to Category Theory by Mark Seemann.
• From Design Patterns to Category Theory at Hacker News.
• Workshop on Applied Category Theory in Leiden/The Netherlands, April 30 – May 4, 2018.
• Workshops: From Design Patterns to Universal Abstractions,
Workshops 2019, at NDC, Sydney, Australia.
• Ambjörn’s archive on category theory at my.confolio.org
• A Networked World by David Spivak, 2019.
• Applied Category Theory Seminar, 2019.
• With Category Theory, Mathematics Escapes From Equality,
by Kevin Hartnett, October 10, 2019.
• Conducting the Mathematical Orchestra from the Middle at an interview with Emily Riehl at Quanta Magazine.
• Emmy Noether – the grandmother of Category Theory.
• Samuel Eilenberg and Saunders Mac Lane – the fathers of Category Theory.
• The Last Mathematician from Hilbert’s Göttingen: Saunders Mac Lane as Philosopher of Mathematics.
• Coherence condition at Wikipedia.
• Categorification and de-categorification at Wikipedia.
• Homology (mathematics) at Wikipedia.
• David Spivak on Category Theory, posted by Simon Willerton at n-category café.
• Category Theory for Programmers – the Preface by Bartosz Milewski, 2014.
•
///////
Key Articles:
• What is a Concept? Joseph Goguen, in Dau, Mugnier & Stumme (Eds), Conceptual Structures: Common Semantics for Sharing Knowledge, Proceedings of the 13th International Conference on Conceptual Structures, Kassel, Germany, July 2005, Springer Verlag, Lecture Notes on Artificial Intelligence (LNAI 3596), ISBN-13 978-3-540-27783-5.
• An Elementary Theory of the Category of Sets (long version) with commentary,
by F. William Lawvere.
• An informal introduction to Topos theory, by Tom Leinster, arXiv, 2011.
• Ologs – A categorical framework for knowledge representation, by David Spivak and Robert Kent, 2016.
///////
A category is a pattern, and a functor is an analogy between two patterns:
///////
Five dogmas of category theory
(Joseph Goguen: A Categorical Manifesto, 1989):
///////
///////
Negozilla:
///////
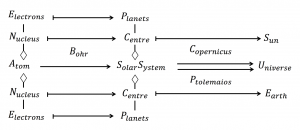
The Bohr-Copernicus functor:
///////
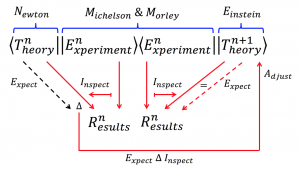
Updating theory through experiment:
(expressed in Knowledge Algebra):
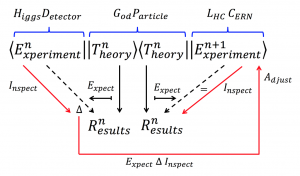
Updating experiment through theory
(expressed in Knowledge Algebra):
///////
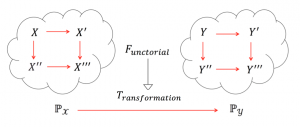
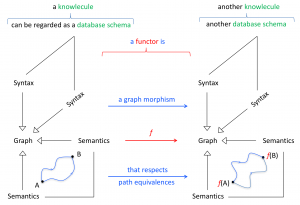
Functorial transformation:
////////
A functorial transformation \, f \, between two knowlecules \, K^1_{now} \, and \, K^2_{now} \, :
Since each path equivalence in the syntactic graph expresses a fact, we can write:
\, [{K^1_{now}}]^{S_{yn}\times S_{yn}}_{S_{em}\times S_{em}} \, \, \xrightarrow[\; that \; respects \; facts \;]{\; graph \; morphism \;} \, [{K^2_{now}}]^{S_{yn}\times S_{yn}}_{S_{em}\times S_{em}} \,///////
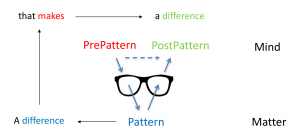
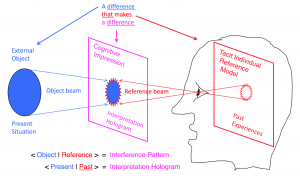
A difference that makes a difference:
///////
How a difference makes a difference:
///////
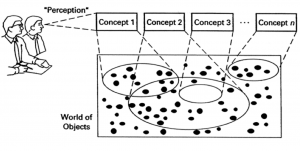
Interpreting objects through concepts:
///////
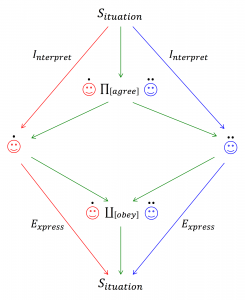
What we agree on and what we obey:
///////
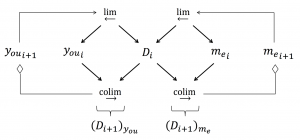
We as the limit and colimit of Me and You:
///////
Interpreting an Object through a Model:
///////
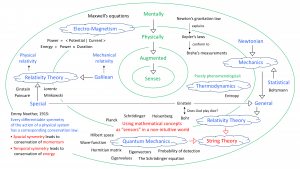
Physically and mentally augmented senses:
///////
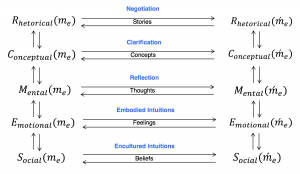
Overview of Human Communication:
///////
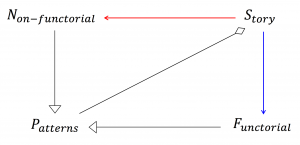
Functorial and non-functorial patterns:
///////
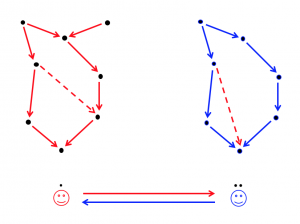
Communicating through thought-graphs:
///////
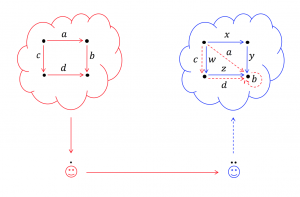
Mapping a thought-square 1:
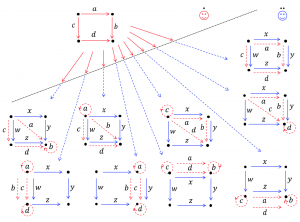
///////
Mapping a thought-square 2:
///////
Mapping a thought-square 3:
///////
Mapping a thought-square 4:
///////
Mapping a thought-square 5:
///////
Mapping a thought-square 6:
///////
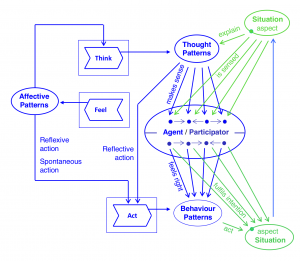
Thoughts and behavior patterns
///////
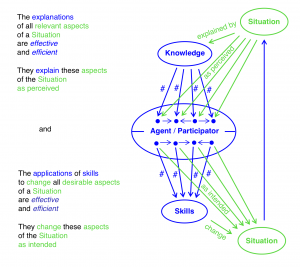
No drivers to learn when all triangles commute
///////
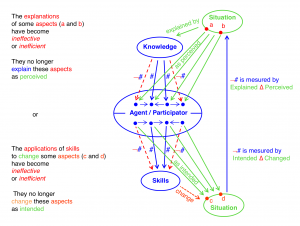
Learning kicks in when some triangles don’t commute
///////
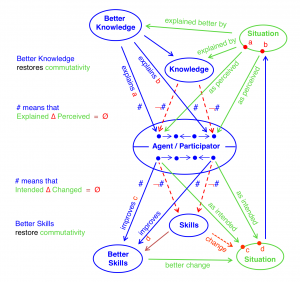
Better knowledge and skills restore commutativity
///////
///////
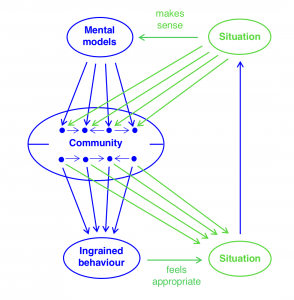
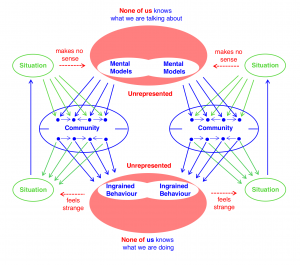
Mental models – Ingrained behavior
///////
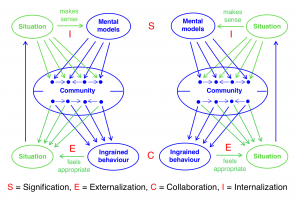
Inter-reflection and inter-action
///////
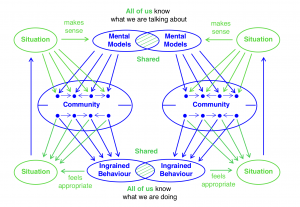
Shared mental models – shared ingrained behavior
///////
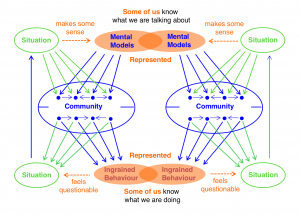
Union and intersection of mental models and ingrained behavior
///////
Unrepresented inter-relation mode
///////
///////
///////