This page is a sub-page of our page on Linear Transformations.
///////
Related pages:
• Shift of Basis for Vectors
• Shift of Basis (in general).
///////
Representation and Reconstruction of a Presentant with respect to a Background
Representation: \, [ \, p_{resentant} \, ]_{B_{ackground}} \, \mapsto \, \left< \, r_{epresentant} \, \right>_{B_{ackground}}
Reconstruction: \, \left( \, \left< \, r_{epresentant} \, \right>_{B_{ackground}} \, \right)_{B_{ackground}} \mapsto \,\, p_{resentant}
/////// In Swedish:
Representation och Rekonstruktion av en Presentant med avseende på en Bakgrund
Representation: \, [ \, p_{resentant} \, ]_{B_{akgrund}} \, \mapsto \, \left< \, r_{epresentant} \, \right>_{B_{akgrund}}
Rekonstruktion: \, \left( \, \left< \, r_{epresentant} \, \right>_{B_{akgrund}} \, \right)_{B_{akgrund}} \mapsto \,\, p_{resentant}
/////// Back to English:
Representation and Reconstruction of a Linear Transformation
with respect to a Basis for its Domain and and a Basis for its Codomain:
Representation: [ \,\, a \, l_{inearMap} \, ]_{a \, B_{asisForItsCodomain}}^{a \, B_{asisForItsDomain}} \, \mapsto \, \left< \, a \, m_{atrix} \, \right>_{a \, B_{asisForItsCodomain}}^{a \, B_{asisForItsDomain}}
Reconstruction: \left( \, \left< \, t_{he} \, m_{atrix} \, \right>_{t_{he} \, B_{asisForItsCodomain}}^{t_{he} \, B_{asisForItsDomain}} \, \right)_{t_{he} \, B_{asisForItsCodomain}}^{t_{he} \, B_{asisForItsDomain}} \, \mapsto \, t_{he} \, l_{inearMap}
///////
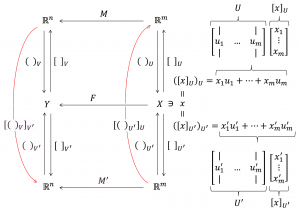
Let \, X \, and \, Y \, be two linear spaces (= vector spaces).
Given a linear map \; F: X \rightarrow Y \; , we can express its action on a vector \, x \in X \, as
\, Y \ni F(x) \leftarrow x \in X .
This reversal of the usual direction in the visual representation of \, F \, is due to advantages in connecting smoothly with matrix algebra, and it is demonstrated in our section on Linear Transformations.
///////////
The Basis-Shift formula for Linear Transformations:
Let \, U \, and \, U' \, be two different bases for \, X ,
and let \, V \, and \, V' \, be two different bases for \, Y .
Hence (from the basis shift formula for vectors) we can write:
U \triangleq \begin{bmatrix} | & & | \\ u_1 & \cdots & u_m \\ | & & | \end{bmatrix}, \; U' \triangleq \begin{bmatrix} | & & | \\ u'_1 & \cdots & u'_m \\ | & & | \end{bmatrix} \, ,
V \triangleq \begin{bmatrix} \, | & & | \\ v_1 & \cdots & v_n \\ | & & | \end{bmatrix}, \; V' \triangleq \begin{bmatrix} \, | & & | \\ v'_1 & \cdots & v'_n \\ | & & | \end{bmatrix} .
From the discussion above we have:
[F(x)]_V \equiv [\, F \,]_V^U \, [\, x \,]_U \,
[F(x)]_{V'} \equiv [\, F \,]_{V'}^{U'} \, [\, x \,]_{U'} \, .
Moreover
[\, x \,]_{U'} \equiv {[B_{asisShift}]}_{U'}^U [x]_U \, , and
[F(x)]_{V'} \equiv {[B_{asisShift}]}_{V'}^V [F(x)]_V \, .
Hence we get
[F(x)]_{V'} \equiv [B_{asisShift}]_{V'}^V [\, F \,]_V^U [B_{asisShift}]_U^{U'} [\, x \,]_{U'} \, ,
and therefore we arrive at
the basis-shift formula for linear transformations:
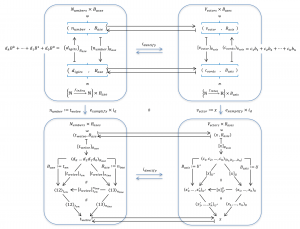
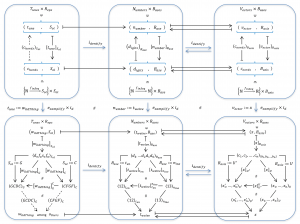
[\, F \,]_{V'}^{U'} \equiv [B_{asisShift}]_{V'}^V [\, F \,]_V^U [B_{asisShift}]_U^{U'} \, .
///////
Change of basis for the domain
and the codomain of a linear transformation:
///////
///////
[\;\;]_U^{U'} \triangleq {[\left( \;\; \right)_{U'}]}_U
[\;\;]_U \equiv [\;\;]_U^{U'} [\;\;]_{U'} \,
[F(x)]_V \equiv [\, F \,]_V^U \, [\, x \,]_U \,
[\, F(x) \,]_{V'} \equiv [\, F \,]_{V'}^{U'} [ \, x \, ]_{U'} \equiv [\;\;]_{V'}^V [\, F \,]_V^U [\;\;]_U^{U'} [ \, x \, ]_{U'} \, .
[\, F \,]_{V'}^{U'} \equiv [\;\;]_{V'}^V [\, F \,]_V^U [\;\;]_U^{U'} \, .
///////
Numbers and Vectors are naturally related to each other:
Hence Numbers and Vectors are naturally equivalent.
Numbers and Vectors are naturally related to Music:
Check out our section on Category Theory
///////