This page is a sub-page of our page on Category Theory.
///////
Related KMR pages:
///////
• The n-Category Café: A group blog on Category Theory by John C. Baez.
• Brendan Fong, The Algebra of Open and Interconnected Systems,
PhD Thesis in Computer Science, University of Oxford, 2016.
/////////////////////////////////////////////////////////
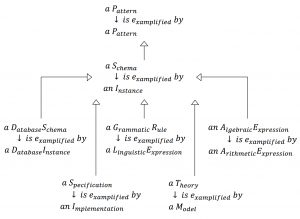
A \, P_{attern} \, is \, e_{xemplified} \, by \, another \, P_{attern} \, :
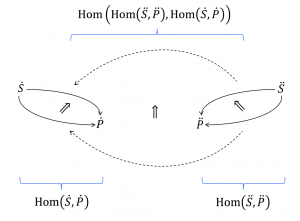
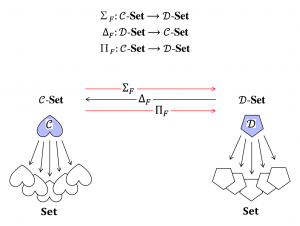
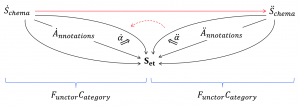
A schema mapping and its corresponding pullback functor:
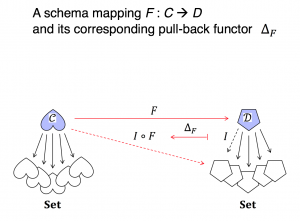
Left and Right Adjoints to Pullback of Schemas:
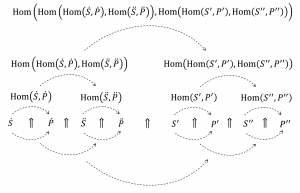
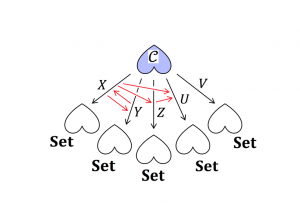
Functor Category of Annotations:
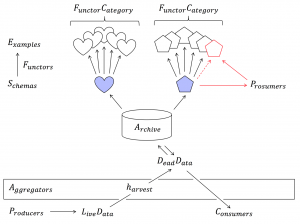
From Aggregators to Functor Categories:
Pullback of an Annotation Schema:
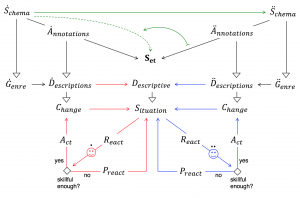
Each annotation is a functor : Schema —> Sets, and the set of annotations on a given schema forms a functor category. A functor category has objects that are themselves functors and arrows that are given by natural transformations between some of these functors.
Pullback of a Functor Category:
Translating from annotation-i to annotation-k:
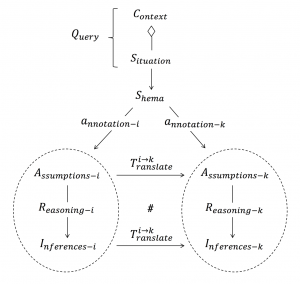
Notation: If the above diagram commutes (as is indicated by the # sign), the \, a_{nnotation-k} \, is said to be naturally related to the \, a_{nnotation-i} \, . Natural relationships are indicated by “implication arrows”, as seen in the diagram below.
Within the metadata (= annotation) community, a naturally related annotation, that is an annotation which an implication arrow is pointing towards, is called a “dumb-down” of the annotation that it is naturally related to, which is the annotation from which the same implication/”dumbification” arrow is pointing away. A dumb-down annotation represents a “coarsification” (= a coarser version) of the original annotation.
Functor categories:
Functor n-categories:
//////
/////////////////// Infrastructures for cross-institutional reasoning, p. 86
10. Databases as functor categories
10.1. Database schemas present categories
10.2. Instances on a schema
10.3. Data migration
10.4. The pullback migration functor ∆
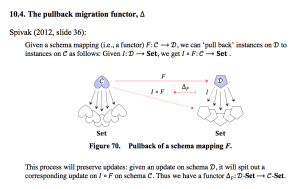
10.5. Functors in three different contexts
10.6. Adjoint functors
10.7. The migration functors are adjoints to the pullback functor
10.8. The ‘product-oriented’ (right) push-forward makes joins
10.9. The ‘sum-oriented’ (left) push-forward makes unions
10.10 Views
/////// Infrastructures for cross-institutional reasoning, p. 489
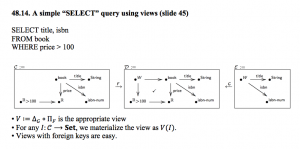
48.14 A simple “SELECT” query using views
48.15 The Grothendieck construction
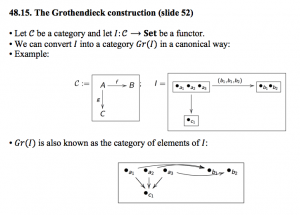
48.16 The Grothendieck construction applied to database instances
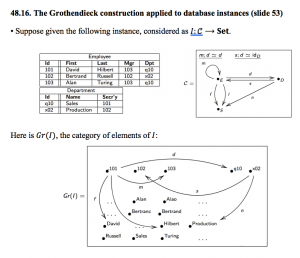
48.17 A different perspective on data
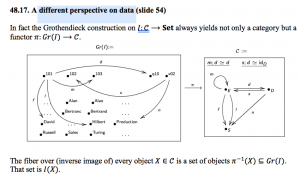
48.18 RDF schema and stores
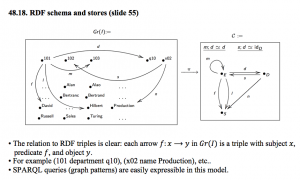
48.19 Allowing for semi-structured data
48.20 Summary
49. EXCERPTS FROM SPIVAK, 2014 (p. 396)
49.0 Comments on Category Theory for the Sciences
49.1. Graphs
49.2. What are databases?
49.3. What is a database schema?
49.4. What is an instance of a database schema?
49.5. The Grothendieck construction
49.6. The Grothendieck construction (example)
49.7. The Grothendieck construction (application)
(cont.)
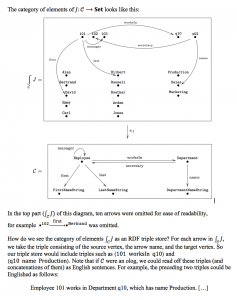
49.8. Slogan 6.2.2.5 for the Grothendieck construction
49.9. Full subcategory
(cont.)
49.10. Comma categories
Example:
49.11. Arithmetic of categories
49.12. The definition of categories
49.13. The category of graphs
49.14. The category of small categories
49.15. Database schemas present categories
49.16 Instances on a schema S
49.17. Groupoids
49.18. The category of propositions
