This page is a sub-page of our page on What is Mathematics?

///////

The historical struggle to get rid of meaning

Mathematics has fought a long and hard historical struggle to rid itself of meaning and express its content as pure form. As expressed by the great mathematician Hermann Weyl at the beginning of the last century:

“We now come to a decisive step of mathematical abstraction: we forget about what the symbols stand for… [The mathematician] need not be idle; there are many operations which he may carry out with these symbols, without ever having to look at the things they stand for“.

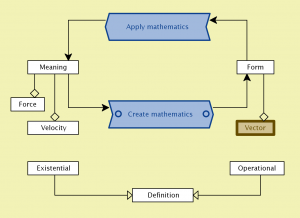
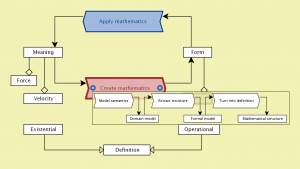
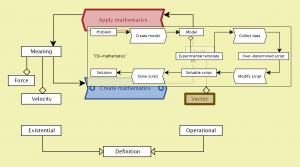
Creating and Applying Mathematics:  the loop between meaning and form:

///////

///////

///////

///////

Meaning is brought back into mathematics by applying it to something, which means interpreting the symbols. Hence applied mathematics can be seen as a transformation process from form to meaning.

However, because of the way the educational systems are structured, we normally fail to explain to students the meaning of being meaningless, which is that we can capture many different meanings in the same form. If, whenever we write a mathematical expression on the board, we were to give at least two different interpretations of the symbols, then this lack of understanding would not appear. As things are, we foster it from the start.

Although well-known to mathematicians and scientists, this fundamental systemic loop between meaning and form is rarely spoken of in math education? Why is that so? There are many underlying causes, but a major reason is that we have a tradition – going back to the old Greeks – of dividing mathematics into “pure” and “non-pure” (= “applied”). These two realms are normally handled by different departments with very different perspectives on mathematics.

Från Mening till Form – Meningen med att vara Meningslös
(Ambjörn Naeve på YouTube):