This page is a sub-page of the page on our review of the book Siffrorna i våra liv by Stefan Buijsman.
///////
Related KMR-pages:
///////
Other relevant sources of information:
• Frequentist probability at Wikipedia.
• Frequentist inference at Wikipedia
• Bayesian probability at Wikipedia.
• Bayesian inference at Wikipedia.
• Bayes theorem, and making probability intuitive, Steven Strogatz on YouTube.
• Probability – The Logic of Science by E.T. Jaynes.
• Convergence of random variables at Wikipedia.
• Convergence of Binomial to Normal: Multiple Proofs, by Subhash Bagui and K.L. Mehra.
• Uncertainty as Applied to Measurements and Calculations by John Denker.
• History of probability at Wikipedia.
• History of statistics at Wikipedia
• The Method of Least Squares at Wikipedia
///////
Kap. 6: Osäkerhetskalkyl handlar om att kunna hantera osäkerheter i de informationsmängder vi interagerar med på olika sätt. Filosofiskt sett har osäkerhetsteorin två olika, oförenliga och historiskt oförsonliga utgångspunkter och metodiker: Den frekventistiska metodiken går ut på att beräkna sannolikheter för olika effekter av en given händelse, medan den Bayesianska metodiken går ut på att beräkna sannolikheten för olika orsaker till en given händelse.
Den effektsannolikhetsbaserade utgångspunkten leder till den frekventistiska sannolikhetsteorin, frekventismen, med sina slumpvariabler, sina utfallsrum och sitt antagande om ett närmande av varje “frekvenskvot” för positiva utfall av en händelse mot en sannolikhet för denna händelse, via ett gränsvärde när antalet försök ökar obegränsat.
Den orsakstrolighetsbaserade utgångspunkten leder till den Baysianska trolighetshetsteorin, Bayesianismen, som har en objektiv och en subjektiv del. Den objektiva Bayesianismen handlar om vetenskapens egen slutledningslogik – baserad på plausible reasoning. Den subjektiva Bayesianismen – eller trolighetsteorin som jag har valt att kalla den här – handlar om förflutna historier av betingade troligheter och olika val utförda på grundval av dessa – storheter som ofta kan beräknas via Bayes sats.
• Bayes theorem, and making probability intuitive, Steven Strogatz on YouTube.
En stor fördel med den Baysianska trolighetsteorin är att den inte behöver vare sig den frekventistiska sannolikhetsteorins utfallsrum eller dess frekvenskvotsbaserade effektsannolikheter. Detta gör det möjligt för “trolighetsingenjörerna” att uppdatera sina troligheter via experimentella erfarenheter. Denna typ av uppdateringar utgör grunden för s.k. maskininlärning – något som ofta (och i mitt tycke missvisande) kallas artificiell intelligens.
Sharon Bertsch McGrayne inleder sin historiska ‘thriller’ The Theory That Would Not Die, som handlar om Baysianismens historiska utveckling, med följande citat från den brittiske ekonomen John Maynard Keynes:
When the facts change, I change my opinion. What do you do, sir?
I både Bertsch McGraynes och Buijsmans böcker kallas såväl objektiva sannolikheter som subjektiva troligheter för “sannolikheter” vilket är helt i enlighet med det etablerade språkbruket. Detta språkbruk innebär dock tyvärr att
det har uppstått en dubbelbetydelse av begreppet sannolikhet.
För att kunna behålla den språkliga precisionen i begreppen och formulera de båda osäkerhetskalkylerna matematiskt är det dock viktigt att skilja mellan begreppen objektiv sannolikhet (= engelskans probability) och subjektiv sannolikhet eller trolighet (= engelskans plausibility). Man kan uppleva det som “troligt” att man kommer att bli överkörd om man springer rätt ut i en intensivt trafikerad gata, men det kan aldrig vara “sannolikt”, eftersom det inte finns någon frekvenskvot – och därmed inte heller någon frekventistisk sannolikhet – för en sådan händelse.
///////
KOMMENTAR (till kap 6 forts (i anslutning till sid 73, rad 4):
Man kan beskriva osäkerhetskalkylens utveckling i ett antal olika steg (som inte är strikt kronologiskt ordnade nedan):
•) Spel om pengar har funnits i tusentals år, men spelteori handlade enbart om intuition och gissningar innan den italienske matematikern (och den entusiastiske spelaren) Girolamo Cardano (1501 – 1576). Han började skriva sin bok Liber de Ludo Aleae (The Book on Games of Chance) – om det som senare skulle komma att kallas “sannolikheter” – innan han fyllt trettio, men avslutade den inte förrän han hade passerat sextio. Boken publicerades år 1563 och innebar den första ansatsen till en matematisk spelteori. Här introducerade Cardano ett bråktal mellan 0 och 1 för begreppet “sannolikhet” för olika utfall vid tärningskast och visade hur man kunde räkna ut sannolikheten för att t.ex. få antingen en femma eller sexa när man kastade en tärning, eller sannolikheten för att få två sexor när man kastade två tärningar.
Cardano var ett universalgeni, som var verksam inom en mängd olika områden. Han uppfann bl.a. kardanaxeln som fortfarance används som drivaxel i nutida fordon. Cardano är mest känd för sin revolutionerande bok om algebra, Ars Magna (The Great Art) från 1545. Den beskriver hur man kan lösa tredje- och fjärdegradsekvationer, bl.a. med hjälp av det som senare kom att kallas komplexa tal. Ars Magna var även den första matematikbok som systematiskt använde sig av negativa tal.
•) Brevväxlingen mellan Fermat och Pascal
•) Jacob Bernoulli (1655 – 1705) beräknade medelvärden av kombinationer av kända sannolikhetsvärden för olika spelutgångar, vilket gjorde att man kunde dela upp en ”spelpott” på ett rationellt sätt – förutsatt att de båda spelarna bedömdes som lika skickliga, dvs att båda bedömdes ha sannolikheten 50% att vinna.
/////// Citat från Wikipedia:
De stora talens lag är en sats inom sannolikhetsteorin, som innebär att det aritmetiska medelvärdet av ett stort antal oberoende observationer av en slumpvariabel med stor sannolikhet ligger nära variabelns väntevärde. De stora talens lag kan sägas motsvara uttrycket “Det jämnar ut sig i det långa loppet”, under vissa omständigheter.
Lagen finns i två olika former, den svaga formen och den starka formen. Den första versionen av de stora talens lag formulerades och bevisades av Jacob Bernoulli i början på 1700-talet men publicerades inte förrän år 1713, åtta år efter hans död. Det Bernoulli visade motsvarar den svaga formen av stora talens lag, med fallet då de ingående slumpvariablerna endast antar två värden, en s.k. binomialfördelning.
Egentligen behandlade Bernoulli det omvända jämfört med hur stora talens lag idag brukar formuleras; givet ett utfall från \, N \, antal försök, hur kan vi då bestämma väntevärdet. (Om vi tar upp \, N \, kulor ur en påse med enbart blåa och gula kulor, vad kan vi då säga om den totala fördelningen?)
/////// Slut på citatet från Wikipedia
Sin nuvarande formulering fick de stora talens lag år 1933 av Andrei Kolmogorov i hans banbrytande verk Foundations of the Theory of Probability som även lade en axiomatisk grund för den frekventistiska sannolikhetsteorin. Genom sina sannolikhetsteoretiska axiom grundade Kolmogorov sin sannolikhetsteori på måtteori via det axiomatiskt införda begreppet sigma-algebra.
///////
•) Abraham de Moivre (1667 – 1754) införde utfallsrum, slumpvariabler och ”utfallssannolikheter” (= gränsvärden av frekvenskvoter) för den diskreta sannolikhetsfördelning som kallas binomialfördelningen och som kan beskrivas genom utfallsfördelningen när man singlar slant med sannolikheten ½ för krona och ½ för klave. År 1718 publicerade de Moivre sina resultat i boken The Doctrine of Chances som grundlade sannolikhetsteorin.
/////// Översätter från Convergence of Binomial to Normal: Multiple Proofs by Bagui and Mehra, 2017.
Det är väl känt (se [5]) att om både \, np \, och \, nq \, är större än \, 5 \, så kan de binomiala sannolikheterna – som ges av sannolikhetsmassefunktionen (pmf) – på ett tillfredsställande sätt approximeras av sannolikhetstäthetsfunktionen (pdf) för den s.k. normalfördelningen.
/////// Slut på översättningen från “Convergence of Binomial to Normal: Multiple Proofs”
Det är denna konvergens som gör att de taggiga kurvorna blir mjukare och mjukare när antalet slantsinglingar ökar. När \, p \, är i närheten av \, \frac {1}{2} \, blir dessa approximationer i själva verket “ganska bra” för \, n \, så litet som \, 10 . De Moivre (1738) var den som först föreslog att approximera binomialfördelningen med en normalfördelning när \, n \, är stort. Hans bevis grundade sig på Stirlings formel.
År 1733 visade de Moivre att när man utför ett obegränsat ökande antal av varandra oberoende slantsinglingsexperiment (med samma antal slantsinglingar i varje försök) så närmar sig binomialfördelningen en gränsfördelning, som idag kallas normalfördelning. De Moivres gränsfördelningsresultat, som formulerades mera strikt av Laplace (1812) var det första exemplet på en av sannolikhetsteorins viktigaste satser, den centrala gränsvärdessatsen och går idag under namnet de Moivre-Laplace sats.
/////// Quoting Wikipedia:
Dutch mathematician Henk Tijms writes:[41]
“The central limit theorem has an interesting history. The first version of this theorem was postulated by the French-born mathematician Abraham de Moivre who, in a remarkable article published in 1733, used the normal distribution to approximate the distribution of the number of heads resulting from many tosses of a fair coin.
This finding was far ahead of its time, and was nearly forgotten until the famous French mathematician Pierre-Simon, marquis de Laplace rescued it from obscurity in his monumental work Théorie analytique des probabilités, which was published in 1812. Laplace expanded De Moivre’s finding by approximating the binomial distribution with the normal distribution.
But as with de Moivre, Laplace’s finding received little attention in his own time. It was not until the nineteenth century was at an end that the importance of the central limit theorem was discerned, when, in 1901, Russian mathematician Aleksandr Lyapunov defined it in general terms and proved precisely how it worked mathematically. Nowadays, the central limit theorem is considered to be the unofficial sovereign of probability theory.”
///////
Sir Francis Galton described the Central Limit Theorem in this way:[42]
“I know of scarcely anything so apt to impress the imagination as the wonderful form of cosmic order expressed by the “Law of Frequency of Error“. The law would have been personified by the Greeks and deified, if they had known of it. It reigns with serenity and in complete self-effacement, amidst the wildest confusion. The huger the mob, and the greater the apparent anarchy, the more perfect is its sway. It is the supreme law of Unreason. Whenever a large sample of chaotic elements are taken in hand and marshalled in the order of their magnitude, an unsuspected and most beautiful form of regularity proves to have been latent all along.”
///////
The actual term “central limit theorem” (in German: “zentraler Grenzwertsatz”) was first used by George Pólya in 1920 in the title of a paper.[43][44] Pólya referred to the theorem as “central” due to its importance in probability theory. According to Le Cam, the French school of probability interprets the word central in the sense that “it describes the behaviour of the centre of the distribution as opposed to its tails”.[44] The abstract of the paper On the central limit theorem of calculus of probability and the problem of moments by Pólya[43] in 1920 translates as follows:
“The occurrence of the Gaussian probability density \, e^{-x^2} \, in repeated experiments, in errors of measurements, which result in the combination of very many and very small elementary errors, in diffusion processes etc., can be explained, as is well-known, by the very same limit theorem, which plays a central role in the calculus of probability. The actual discoverer of this limit theorem is to be named Laplace; it is likely that its rigorous proof was first given by Tschebyscheff and its sharpest formulation can be found, as far as I am aware of, in an article by Liapounoff.”
/////// End of quote from Wikipedia
•) Thomas Simpson (1710 – 1761) ”vände” på sannolikhetskalkylen och koncentrerade sig på att summera sannolikheterna för (mät)fel – i stället för sannolikheterna för (mät)rätt vilket leder till medelvärden. Detta ledde via bl.a. Carl-Friedrich Gauss till den s.k. minstakvadratmetoden för minimering av summan av de totala mätfelen. Minstakvadratmetoden tillskrivs vanligen Gauss men publicerades först av Adrien-Marie Legendre.
•) Thomas Bayes (1701 – 1761) kom på ett listigt sätt att räkna ut de nödvändiga troligheterna genom att använda sig av det teorem som bär hans namn (Bayes sats) och som publicerades först efter hans död.
•) Pierre-Simon Laplace (1749 – 1827) utvecklade och populariserade både den frekventistiska och den Bayesianska statistiken, samt mycket annan matematik. Laplace var en av sin tids mest betydande matematiker och hans Celestial Mechanics (i fem volymer) vidareutvecklade Newtons ideer från Principia med hjälp av Leibniz version av differential- och integralkalkylen samt egna utvidgningar av denna.
Tillsammans med matematiker som Leonard Euler, Joseph-Louis Lagrange, Peter Gustav Lejeune Dirchlet och Siméon Denis Poisson bidrog Laplace till utvecklingen av olika verktyg för att lösa partiella differentialekvationer bl.a. variationskalkyl, Laplacetransform och tekniken med s.k. genererande funktioner. En av de viktigaste partiella differentialekvationerna inom fysiken går under namnet Laplace ekvation eftersom Laplace var den förste som studerade den.
/////// Quoting Wikipedia:
In probability theory, the central limit theorem (CLT) establishes that, in some situations, when independent random variables are added, their properly normalized sum tends toward a normal distribution (informally a “bell curve”) even if the original variables themselves are not normally distributed. The theorem is a key concept in probability theory because it implies that probabilistic and statistical methods that work for normal distributions can be applicable to many problems involving other types of distributions.
For example, suppose that a sample is obtained containing a large number of observations, each observation being randomly generated in a way that does not depend on the values of the other observations, and that the arithmetic mean of the observed values is computed. If this procedure is performed many times, the central limit theorem says that the distribution of the average will be closely approximated by a normal distribution. A simple example of this is that if one flips a coin many times the probability of getting a given number of heads in a series of flips will approach a normal curve, with mean equal to half the total number of flips in each series. (In the limit of an infinite number of flips, it will equal a normal curve.)
The central limit theorem has a number of variants. In its common form, the random variables must be identically distributed. In variants, convergence of the mean to the normal distribution also occurs for non-identical distributions or for non-independent observations, given that they comply with certain conditions.
The earliest version of this theorem, that the normal distribution may be used as an approximation to the binomial distribution, is now known as the de Moivre–Laplace theorem.
/////// End of quote from Wikipedia
/////// Quoting Investopedia:
Understanding the Central Limit Theorem (CLT)
According to the central limit theorem, the mean of a sample of data will be closer to the mean of the overall population in question as the sample size increases, notwithstanding the actual distribution of the data, and whether it is normal or non-normal. This concept was first discovered by Abraham de Moivre in 1733 though it wasn’t named until George Polya, in 1920, dubbed it the Central Limit Theorem.
As a general rule, sample sizes equal to or greater than 30 are considered sufficient for the CLT to hold, meaning the distribution of the sample means is fairly normally distributed. So, the more samples that one takes results in the graph looking more and more like that of a normal distribution.
Another key aspect of CLT is that the average of the sample means and standard deviations will equal the population mean and standard deviation. This is extremely useful in predicting the characteristics of a population with a high degree of accuracy.
Key Takeaways:
• The central limit theorem (CLT) states that the distribution of sample means approximates a normal distribution as the sample size gets larger.
• Sample sizes equal to or greater than 30 are considered sufficient for the CLT to hold.
• A key aspect of CLT is that the average of the sample means and standard deviations will equal the population mean and standard deviation.
• A sufficiently large sample size can predict the characteristics of a population accurately.
/////// End of quote from Investopedia
Sid 70, rad 9: Matematiken kring sannolikhet började alltså med spel. Och med tiden blev den alltmer praktisk. Redan Bernoulli försökte beräkna något som även kunde vara till nytta. Han kommer då också lite närmare en lösning; man behöver inte längre veta vad alla amerikaner tycker och tänker för att göra en opinionsmätning. Ändå måste man redan på förhand arbeta med antagandet att Clinton kommer att få 52 procent av rösterna, och därigenom är det inte mycket mer praktiskt. I början vet vi ju inte hur hela landet kommer att rösta. Den gissningen vill man alltså inte göra och som tur är behövs inte det heller. Detta tack vare de idéer som utarbetades av näste matematiker, Abraham de Moivre, på basis av något som vi alla associerar med sannolikhet: krona eller klave.
KOMMENTAR: Problemet är att författaren hoppar över tre grundläggande steg i framväxten av de begrepp som möjliggör moderna sannolikhetsberäkningar:
(i) infinitesimalkalkylens fundamentalsats
(ii) de stora talens lag
(iii) den centrala gränsvärdessatsen.
Därmed blir det i stort sett omöjligt att beskriva utvecklingen på ett begripligt sätt.
För att kunna förklara de stora talens lag och den centrala gränsvärdessatsen
behöver man stödja sig på följande grundläggande begrepp inom sannolikhetsläran:
• slumpvariabel (= ”stokastisk variabel”)
• (kumulativ) fördelningsfunktion
• frekvensfunktion (= täthetsfunktion)
och för att förstå relationerna mellan fördelningsfunktionen och frekvensfunktionen för en slumpvariabel måste man stödja sig på infinitesimalkalkylens fundamentalsats.
///////
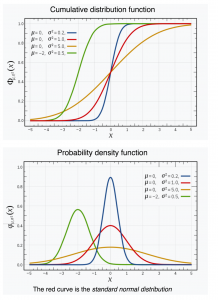
Image source: https://en.wikipedia.org/wiki/Normal_distribution
///////
Från infinitesimalkalkylens fundamentalsats följer att derivatan av den kumulativa fördelningsfunktionen för en slumpvariabel är lika med slumpvariabelns frekvensfunktion (= täthetsfunktion).
///////
(1): Värdet av den kumulativa fördelningsfunktionen \, F \, för en slumpvariabel i en punkt \, x ,
dvs \, F(x) , beskriver sannolikheten för att slumpvariabeln antar ett värde
som är mindre än eller lika med \, x .
(2): Värdet av frekvensfunktionen \, f \, för en slumpvariabel i en punkt \, x ,
dvs \, f(x) , är proportionellt mot sannolikheten att slumpvariabeln antar ett värde
inom det infinitesimala (= ”oändligt lilla”) intervallet \, dx \, omkring punkten \, x .
Denna sannolikhet är lika med \, f(x) dx .
///////
Med hjälp av infinitesimalkalkylens fundamentalsats kan man alltså dra följande slutsater:
(1): Värdet av den (kumulativa) fördelningsfunktionen \, F \, i punkten \, x \, ,
dvs \, F(x) , är lika med integralen av frekvensfunktionen \, f(t) \,
över alla värden på \, t \, som är mindre än eller lika med \, x .
(2): Värdet av frekvensfunktionen (= täthetsfunktionen) \, f \, i punkten \, x ,
dvs \, f(x) , är lika med värdet av derivatan av fördelningsfunktionen \, F \, i punkten \, x .
///////
Sammanfattning:
De stora talens lag säger att det aritmetiska medelvärdet av många oberoende observationer av en slumpvariabel med stor sannolikhet ligger nära variabelns väntevärde.
Den centrala gränsvärdessatsen säger att fördelningen av medelvärden av många försök ALLTID blir normal – även om medelvärdesfördelningen i varje försök inte är det.
Vid beräkning av väntevärdet för en summa av oberoende och likafördelade slumpvariabler skapar dessa två fundamentala statistiska krafter – när antingen antalet slumpvariabler eller antalet försök ökar – en konvergens mot en s.k. normal distribution (eller normalfördelning) som beskrivs av en normalfördelningskurva (eng: bell curve).
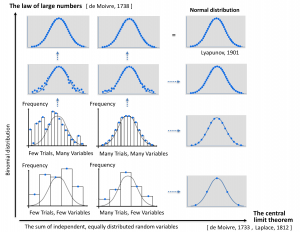
Bearbetning av ett diagram från Mathematics illuminated: Making Sense of Randomness.
Hur dessa strukturer kan utnyttjas för att skapa bättre förståelse och bättre analyser
av idrottsstatistik beskrivs på webbplatsen Tabmathletics .
///////
Properties of the normal distribution
Cumulative Distribution Function (CDF) of the normal distribution
Cramér’s decomposition theorem is equivalent to saying that the convolution of two distributions is normal if and only if both are normal.
Cramér’s decomposition theorem implies that a linear combination of independent non-Gaussian variables will never have an exactly normal distribution, although it may approach it arbitrarily closely.
///////
Nice Blog,Thank you for sharing a valuable topic.